理论-读书笔记1-机器学习实战-kNN,决策树
0,总览
- 数据挖掘十大算法/~2007:C4.5决策树、K-均值(k-means)、支持向量机(SVM)、Apriori、最大期望算法(EM)、PageRank算法、AdaBoost算法、k-近邻算法(KNN)、朴素贝叶斯算法(NB)、分类回归树(CART)
- 本书没有包含:最大期望算法(EM)、PageRank算法
- 本书额外包含:Logistic回归算法、FP-Growth算法、主成分分析、奇异值分解
1,k-近邻算法(K-nearest neighbors / KNN)
-
原理:存在一个样本数据集/训练样本集,样本集中的每个数据都存在标签;输入没有标签的新数据后,将新数据的特征与样本集中数据对应的特征进行比较,选择k个最相似数据中出现次数最多的分类作为新数据的分类;通常k是不大于20的整数,这也是KNN中k的出处。
-
算法流程:
- 特征归一化
- 计算距离
- 对距离排序
- 选择距离最小的k个点,并给出结果
-
总结:
- kNN是分类数据最简单最有效的算法。kNN是基于实例的学习,使用算法时必须有接近实际数据的训练样本数据。
- 注意事项
- 当特征量纲差别很大时,首先要对特征进行归一化以使各特征之间具有可比性
- 改变k的值、训练样本、训练样本的数目、距离度量准则都会对结果产生影响
- kNN的存储空间和计算时间的开销比加大,存不存在一种算法可以减少这两种开销呢?k决策树(可以视为kNN的优化版,可以节省大量计算开销)
- 缺陷:
- kNN必须保存全部数据集,如果训练数据集很大,必须使用大量的存储空间
- 由于必须对数据集中的每个数据计算距离值,实际使用可能非常耗时
- kNN无法给出任何数据的基础结构信息,因此也无法通过kNN直消平均实例样本和典型事例样本具有什么特征(不过求个均值也在某种程度上算是原型了╮(╯▽╰)╭)
-
一些例子
'''例子1:模板''' import numpy as np def kNN(dataIn, trainSet, labels, k): trainSetSize = trainSet.shape[0] '''距离计算''' diffMat = np.tile(dataIn, (trainSetSize, 1)) - trainSet sqDiffMat = diffMat ** 2 sqDistances = sqDiffMat.sum(axis=1) distances = sqDistances ** 0.5 '''对距离排序''' sortedDistIndicies = distances.argsort() '''选择距离最小的k个点,并给出分类结果''' classCount = {} for i in range(k): voteLabel = labels[sortedDistIndicies[i]] classCount[voteLabel] = classCount.get(voteLabel, 0) + 1 sortedClassCount = sorted(classCount.items(), key=lambda x:x[1], reverse=True) return sortedClassCount[0][0] if __name__ == '__main__': dataIn = [0, 0] trainSet = np.array([[1.0, 1.1], [1.0, 1.0], [0, 0], [0, 0.1]]) labels = ['A', 'A', 'B', 'B'] k = 3 print(kNN(dataIn, trainSet, labels, k))'''例子2:min-max归一化''' import numpy as np def minMaxNorm(dataset): minVals = np.min(dataset, axis=0) #注意取最小值的维度,是要取某特征在所有样本中的最小值,而不是某样本所有特征的最小值 maxVals = np.max(dataset, axis=0) return (dataset-minVals) / (maxVals - minVals) if __name__ == '__main__': data = np.random.randint(0, 10, (5, 5)) print(data) print(minMaxNorm(data))例子3需要下载手写数字数据集
'''先观察一下数据,这里用的是8*8的数据集,图像比较粗糙''' import numpy as np from matplotlib import pyplot as plt plt.rcParams['font.family'] = 'Times New Roman' plt.rcParams['font.size'] = 15 dataTrain = np.loadtxt('optdigits.tra', delimiter=',') for i in range(9): plt.subplot(3, 3, i+1) plt.imshow(dataTrain[i, :-1].reshape(8, 8)) plt.title(dataTrain[i, -1]) plt.tight_layout() plt.savefig('numbers.png', dpi=300) plt.show()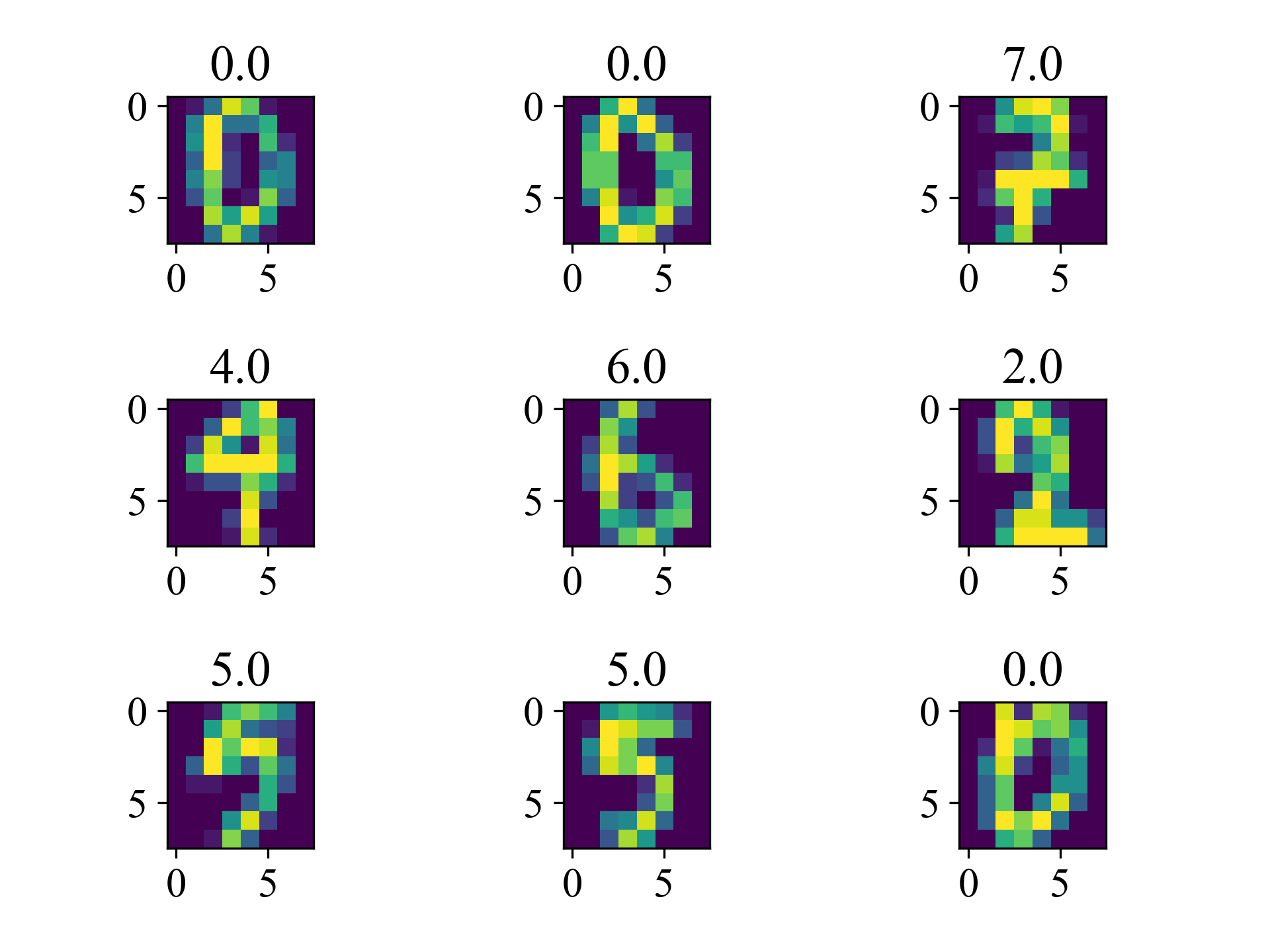
'''分类,转为一维后直接调用前面所用的knn即可''' from knn import kNN import numpy as np '''加载数据''' dataTrain, labels = np.loadtxt('optdigits.tra', delimiter=',')[:, :-1], np.loadtxt('optdigits.tra', delimiter=',')[:, -1] dataTest, correctRes = np.loadtxt('optdigits.tes', delimiter=',')[:, :-1], np.loadtxt('optdigits.tes', delimiter=',')[:, -1] for k in range(1, 10): '''分类''' preRes = [kNN(dataIn, dataTrain, labels, k) for dataIn in dataTest] '''计算正确率''' print(f'k={k}, 正确率为{sum(preRes==correctRes) / len(correctRes) * 100}%')
2,决策树(Decision tree)
-
概念及原理
- 决策树流程图:长方形代表判断模块(decision block),椭圆形代表终止模块(terminating block),从判断模块引出的左右箭头称为分支(branch)
- 原理:根据数据集创建规则,从原始数据中构造决策树。在构造决策树时,需要解决的第一个问题是:当前数据集上哪个特征在划分数据时起决定性作用。为此,我们必须评估每个特征,并在完成评估后将原始数据集划分为几个数据子集,这些数据子集分布在第一个决策点的所有分支上。如果某个分支下的数据属于同一类型,则该数据子集已经完成分类,无需进一步对数据集进行分割;如果某个分支下的数据不属于同一类型,则需要重复划分数据子集的过程,直到所有具有相同类型的数据均在一个数据子集内。
- ID3(Iterative Dichotomiser 3/迭代二分法3)算法:用于生成决策树的算法之一,为C4.5算法的前身。ID3 算法以原始集合\(S\)作为根节点开始,在算法的每次迭代中,它遍历集合\(S\)的每个未使用的属性并计算熵\(H(S)\)或该属性的信息增益\(IG(S)\);然后它选择具有最小熵(或最大信息增益)值的属性; 集合\(S\)然后被选定的属性分割或分区以产生数据子集,并对每个子集进行递归,在递归时只考虑之前为选择过的属性。 在满足以下条件之一时,递归停止:
- 子集中的每个元素都属于同一类。在这种情况下,每个子集由各自独有的类进行标记。
- 没有更多的属性可供选择,但子集中的每个元素并不属于同一类。在这种情况下,每个子集由子集中最常见的示例类进行标记。
- 子集中没有样本(例如人口中没有一个年龄超过 100 岁的人,而分割点是100岁),此时由父节点集中最常见的示例类进行标记。
- 概念及计算公式:
- 自信息:\(l(x_i)=-log_2p(x_i)\)
- 信息熵:\(H(S)=\displaystyle \sum_{x\in{S}}-p(x)log_2p(x)\),当\(H(S)=0\)时,\(S\)被完美划分,此时\(S\)中的所有样本都属于同一类。在ID3中,具有最小熵的属性用于在此迭代中拆分集合 \(S\)。
- 信息增益:\(IG(S,A)=H(S)-\displaystyle \sum_{t\in{T}}p(t)H(t)=H(S)-H(S|A)\),用于度量使用\(A\)拆分\(S\)后,不确定性减少了多少。\(T\)是由特征\(A\)拆分\(S\)后所获得的子集:\(S=\displaystyle \bigcup_{t\in{T}}t\);\(p(t)\)是子集\(t\)中样本的数目占集合\(S\)中样本数目的比例。在DI3中, 具有最大信息增益的属性用于在此迭代中拆分集合\(S\)。
-
一些例子
'''例子1,计算信息熵,熵越高数据越混乱,类别越多''' import math def calcShannonEnt(dataset): totalNum = len(dataset) '''统计数据集中各样本的数目''' numPerClass = {} for data in dataset: currentClass = data[-1] if currentClass not in numPerClass.keys(): numPerClass[currentClass] = 0 numPerClass[currentClass] += 1 '''计算信息熵''' shannonEnt = 0 for key in numPerClass: prob = numPerClass[key] / totalNum shannonEnt += -prob * math.log(prob, 2) return shannonEnt if __name__ == '__main__': dataSet = [ [1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no'], # [0, 0, 'maybe'] #仅增加一类一个样本,结果y ] print(calcShannonEnt(dataSet))'''例子2,根据信息增益选择最适于划分的特征''' import operator from entropy import calcShannonEnt def splitDataset(dataset, axis, value): '''划分数据集,这里是根据选定特征及其值划分特定的数据集''' retDataSet = [] for featVec in dataset: if featVec[axis] == value: reducedFeatureVec = featVec[:axis] reducedFeatureVec.extend(featVec[axis+1:]) retDataSet.append(reducedFeatureVec) return retDataSet def chooseBsetFeatureToSplit(dataset, labels): '''选择数据集中用于特征能够产生最高信息增益的特征''' numFeatures = len(dataset[0]) - 1 #注意是特征的数目 baseEntropy = calcShannonEnt(dataset) bestInfoGain = 0 bestFeature = -1 for i in range(numFeatures): featureList = [example[i] for example in dataset] #统计某一特征的所有值 uniqueVals = set(featureList) newEntropy = 0 for value in uniqueVals: subDataset = splitDataset(dataset, i, value) prob = len(subDataset) / len(dataset) newEntropy += prob * calcShannonEnt(subDataset) #根据特征划分数据集;熵的计算则只是纯粹的与数据集中样本的类别有关 infoGain = baseEntropy - newEntropy if infoGain > bestInfoGain: bestInfoGain = infoGain bestFeature = labels[i] return bestFeature if __name__ == '__main__': myData = [ [1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no'], ] labels = ['no surfacing', 'flippers'] print(chooseBsetFeatureToSplit(myData, labels))'''例子3,递归构建决策树。递归结束的条件是:程序遍历完所有划分数据集的属性(按照目前的算法,此时特征已经减无可减了),或者每个分支下的所有实例都具有相同的分类。''' from collections import Counter from entropy import calcShannonEnt def splitDataset(dataset, axis, value): '''划分数据集,这里是根据选定特征及其值划分特定的数据集''' retDataSet = [] for featVec in dataset: if featVec[axis] == value: reducedFeatureVec = featVec[:axis] reducedFeatureVec.extend(featVec[axis+1:]) retDataSet.append(reducedFeatureVec) return retDataSet def chooseBsetFeatureToSplit(dataset, labels): '''选择能够产生最高信息增益的特征''' numFeatures = len(dataset[0]) - 1 #注意是特征的数目 baseEntropy = calcShannonEnt(dataset) bestInfoGain = 0 bestFeature = -1 for i in range(numFeatures): featureList = [example[i] for example in dataset] #统计某一特征的所有值 uniqueVals = set(featureList) newEntropy = 0 for value in uniqueVals: subDataset = splitDataset(dataset, i, value) prob = len(subDataset) / len(dataset) newEntropy += prob * calcShannonEnt(subDataset) #根据特征划分数据集;熵的计算则只是纯粹的与数据集中样本的类别有关 infoGain = baseEntropy - newEntropy if infoGain > bestInfoGain: bestInfoGain = infoGain bestFeature = labels[i] return bestFeature def majorityCnt(classList): '''返回所有类别中个数最多的类:如果数据集已经处理了所有的属性,但是类标签依然不是唯一的,采用多数表决的方法决定该叶子节点的分类''' classSorted = sorted(Counter(classList), key=lambda x:Counter(classList)[x], reverse=True) return classSorted[0] def createTree(dataset, labels): '''创建树''' classList = [example[-1] for example in dataset] if classList.count(classList[0]) == len(classList): '''终止条件1:类别完全相同时停止继续划分''' return classList[0] if (len(dataset[0])) == 1: '''终止条件2:遍历完所有特征后返回出现次数最多的类别做为该叶子节点的分类''' return majorityCnt(classList) bestFeature = chooseBsetFeatureToSplit(dataset, labels) #用于划分的最佳特征 myTree = {bestFeature: {}} if __name__ == '__main__': myData = [ [1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no'], ] labels = ['no surfacing', 'flippers'] print(chooseBsetFeatureToSplit(myData, labels))
行动是治愈恐惧的良药,而犹豫拖延将不断滋养恐惧。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号