自助法随机采样过程中，对n个样本进行n次有放回的随机采样，当n趋向于无穷大时，最终有多少数据从未被选择过？

1，推导

一个样本在一次抽样过程中未被抽中的概率为

\[(1- \frac{1}{n}) \tag{1} \]

n次抽样均为被抽中的概率为

\[(1-\frac{1}{n})^n \tag{2} \]

当n趋向于无穷大时的概率为

\[\lim_{n \to \infty} (1-\frac{1}{n})^n \tag{3} \]

已知

\[\lim_{n \to \infty} (1+\frac{1}{n})^n=e \tag{4} \]

由（3）、（4）可得：

\[\lim_{n \to \infty}(1-\frac{1}{n})^n = \lim_{n\to\infty}(\frac{1}{(1+\frac{1}{n-1})^n})=\frac{1}{\lim_{n \to \infty(1+\frac{1}{n-1})^{n-1}}}\cdot\frac{1}{\lim_{n\to\infty}(1+\frac{1}{n-1})}=\frac{1}{e}\approx0.368 \tag{5} \]

因此，当样本很大时，有大约36.8%的样本从未被选择过

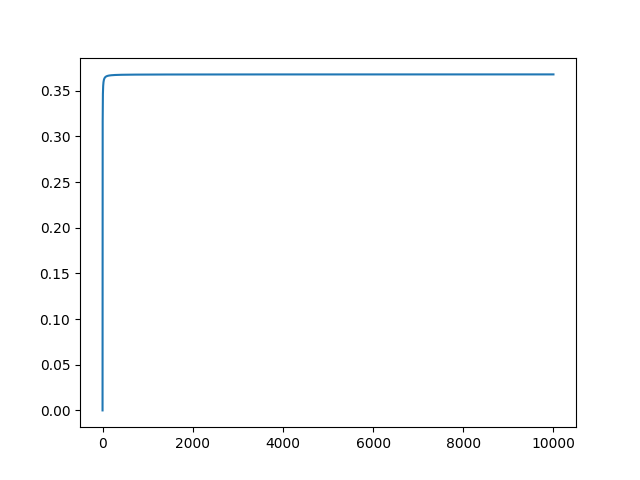
2，代码验证（极限近似求值）

import numpy as np
from matplotlib import pyplot as plt
x = range(1, 10000)
y = [pow((i-1)/i, i) for i in x]
plt.plot(x, y)
plt.show()
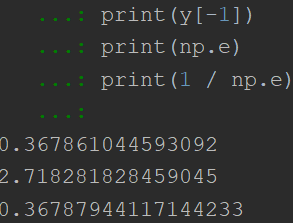
print(y[-1])
print(np.e)
print(1 / np.e)

3，代码验证（随机采样）

import numpy as np
n = 100000
choosen = set()
for i in range(n):
    choosen.add(np.random.randint(1, n+1, 1)[0])
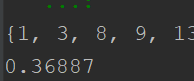
print(choosen)
print(len([i for i in range(1, n+1) if i not in choosen]) / n)