排序算法
1、插入排序(Insertion Sort)
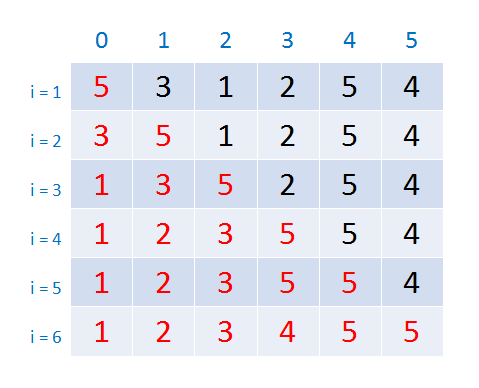
基本思路:将一个记录插入到已排序好的有序表中,从而得到一个新的有序表。即:先将序列的第1个记录看成是一个有序的子序列,然后从第2个记录逐个进行插入,直至整个序列有序为止。
1 void InsertSort(int a[]) { 2 for(int i = 1; i < a.length; i++){ 3 if(a[i] < a[i-1]){ //若小于则移动表后插入,大于则不做处理,即等于直接插入。 4 int j = i-1; //记录待插入的位置,j最终可能是i-1,也可能小于i-1 5 int x = a[i]; //存储待插入的元素,即待排序元素 6 a[i] = a[i-1]; //后移待插入位置的元素一个位置 7 while(j>=0 && x < a[j]){ //查找在有序表的插入位置 8 a[j+1] = a[j]; //后移元素 9 j--; //元素后移,更改待插入位置 10 } 11 a[j+1] = x; //插入到正确位置 12 } 13 } 14 }
2、快速排序(Quick Sort)
基本思路:选取数列中一个数为基准,将数列分成两部分,其中一部分的所有元素比另一部分的所有元素都要大,然后再按照此方式对这两部分进行排序。排序过程可以用递归进行,以此达到有序。
如无序数列 [6 9 2 7 1 8 3 4 5]
a、先把第一项 [6] 取出来,依次与其它项比较,比 [6] 小的放在前面,比 [6] 大的放在后面。
则数列变为 [2 1 3 4 5 6 9 7 8],即 [2 1 3 4 5 6] 与 [9 7 8] 两部分。
b、继续对这两部分数列按照a的方式排序,重复若干次后数列变为有序。
1 static int partition(int[] unsorted, int start, int end) 2 { 3 int pivot = unsorted[start]; 4 while (start < end) 5 { 6 while (start < end && unsorted[end] > pivot) end--; 7 unsorted[start] = unsorted[end]; 8 while (start < end && unsorted[start] <= pivot) start++; 9 unsorted[end] = unsorted[start]; 10 } 11 unsorted[start] = pivot; 12 return start; 13 } 14 15 static void quickSort(int[] unsorted, int start, int end) 16 { 17 if (start < end) 18 { 19 int loc = partition(unsorted, start, end); 20 quickSort(unsorted, start, loc - 1); 21 quickSort(unsorted, loc + 1, end); 22 } 23 } 24 25 static void Main(string[] args) 26 { 27 int[] x = { 6, 2, 4, 1, 5, 9 }; 28 quickSort(x, 0, x.Length - 1); 29 }
3、选择排序(Selection Sort)
基本思路:每次都从待排序区间选出来最小的元素,然后将这个元素与该区间第一个元素交换位置。
1 static void selectionSort(int[] unsorted) 2 { 3 for (int i = 0; i < unsorted.Length; i++) 4 { 5 int min = unsorted[i], min_index = i; 6 for (int j = i; j < unsorted.Length; j++) 7 { 8 if (unsorted[j] < min) 9 { 10 min = unsorted[j]; 11 min_index = j; 12 } 13 } 14 if (min_index != i) 15 { 16 int temp = unsorted[i]; 17 unsorted[i] = unsorted[min_index]; 18 unsorted[min_index] = temp; 19 } 20 } 21 } 22 23 static void Main(string[] args) 24 { 25 int[] x = { 6, 2, 4, 1, 5, 9 }; 26 selectionSort(x); 27 }
4、桶排序(Bucket Sort)
基本思路:根据元素范围创建一个新数组,遍历待排序数组的每一项并将其放入到新数组中,遍历完成后排序完成。
1 static int[] bucketSort(int[] unsorted, int maxNumber = 99) 2 { 3 int[] sorted = new int[maxNumber + 1]; 4 for (int i = 0; i < unsorted.Length; i++) 5 { 6 sorted[unsorted[i]] = unsorted[i]; 7 } 8 return sorted; 9 } 10 11 static void Main(string[] args) 12 { 13 int[] x = { 99, 65, 24, 47, 50, 88,33, 66, 67, 31, 18 }; 14 var sorted = bucketSort(x, 99); 15 }
5、基数排序(Radix Sort)
基本思路:类似于桶排序,但这里需要的桶总是10个,先按个位数进行装桶,再按十位装桶、百位装桶,所有位数都装过桶后排序完成。
1 static void radixSort(int[] unsorted, int array_x = 10, int array_y = 100) 2 { 3 for (int i = 0; i < array_x/* 最大数字不超过999999999...(array_x个9) */; i++) 4 { 5 int[,] bucket = new int[array_x, array_y]; 6 foreach (var item in unsorted) 7 { 8 int temp = (item / (int)Math.Pow(10, i)) % 10; 9 for (int l = 0; l < array_y; l++) 10 { 11 if (bucket[temp, l] == 0) 12 { 13 bucket[temp, l] = item; 14 break; 15 } 16 } 17 } 18 for (int o = 0, x = 0; x < array_x; x++) 19 { 20 for (int y = 0; y < array_y; y++) 21 { 22 if (bucket[x, y] == 0) continue; 23 unsorted[o++] = bucket[x, y]; 24 } 25 } 26 } 27 } 28 29 static void Main(string[] args) 30 { 31 int[] x = {999999999, 65, 24, 47, 13, 50, 92, 88, 66, 33, 22445, 10001, 624159, 624158, 624155501}; 32 radixSort(x); 33 }
6、鸽巢排序(Pigeonhole Sort)
基本思路:类似于桶排序,比桶排序更利于记录重复数据,根据范围创建一个数组,数组索引的位置就表示值,数组里的值表示这个数出现的次数。
1 static int[] pogeon_sort(int[] unsorted, int maxNumber = 10) 2 { 3 int[] pogeonHole = new int[maxNumber + 1]; 4 foreach (var item in unsorted) 5 { 6 pogeonHole[item]++; 7 } 8 return pogeonHole; 9 } 10 11 static void Main(string[] args) 12 { 13 int[] x = { 99, 65, 24, 47, 47, 50, 99, 88, 66, 33, 66, 67, 31, 18, 24 }; 14 var sorted = pogeon_sort(x, 99); 15 }



