Given two words (beginWord and endWord), and a dictionary's word list, find the length of shortest transformation sequence from beginWord to endWord, such that:
- Only one letter can be changed at a time.
- Each transformed word must exist in the word list. Note that beginWord is not a transformed word.
Note:
- Return 0 if there is no such transformation sequence.
- All words have the same length.
- All words contain only lowercase alphabetic characters.
- You may assume no duplicates in the word list.
- You may assume beginWord and endWord are non-empty and are not the same.
Example 1:
Input: beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"] Output: 5 Explanation: As one shortest transformation is "hit" -> "hot" -> "dot" -> "dog" -> "cog", return its length 5.
Example 2:
Input: beginWord = "hit" endWord = "cog" wordList = ["hot","dot","dog","lot","log"] Output: 0 Explanation: The endWord "cog" is not in wordList, therefore no possible transformation.
这是很典型的单源头广度优先搜索最短路径的问题,只要想到这里,结合图的知识就很好做了。怎么构建图呢?首先图的顶点显而易见,就是每一个单词。那么顶点之间的边呢?就是如果顶点的单词互相只差一个字母,顶点间就会形成边。用第一个例子绘制的图如下:
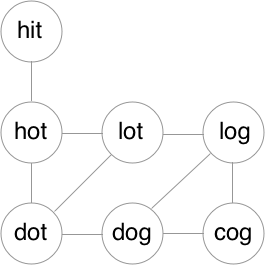
那么根据广度优先搜索的步骤,构建一个队列,之后先把源顶点加入队列,以队列是否为空作为条件开始循环:如果队列不为空,逐个取出队列中的顶点,并把它们标记为“已访问”。对于每个取出的顶点,依次把它未访问的顶点加入队列,直到找到目标顶点或者所有顶点都访问完毕。因为此题只是求最短路径的长度,而不是路径上都有哪些顶点,所以只需要存储每访问一个顶点时该顶点处在路径的位置即可。这里我用了HashMap<String, Integer>。如果是需要存储最短路径本身,那么需要建立数据结构依次存储每个顶点的前驱,并在最后追溯前驱获得路径上的所有顶点。
这里我用一个HashSet替换掉题目中存储单词的List数据结构,只是为了搜索的时候能够快一点。至于如何获取某个节点的邻接节点,即和它只差一个字母的单词,这里用了最暴力的办法,就是把顶点单词的每一位换成其他的25个字母,看看它在不在题目提供的字典里。详细的标注都已经标注在代码中,见下。
Java
class Solution { public int ladderLength(String beginWord, String endWord, List<String> wordList) { HashSet<String> wordSet = new HashSet<>(wordList); //替换掉题目中List结构,加速查找 if (!wordSet.contains(endWord)) return 0; //如果目标顶点不在图中,直接返回0 HashMap<String, Integer> map = new HashMap<>(); //用来存储已访问的节点,并存储其在路径上的位置,相当于BFS算法中的isVisted功能 Queue<String> q = new LinkedList<>(); //构建队列,实现广度优先遍历 q.add(beginWord); //加入源顶点 map.put(beginWord, 1); //添加源顶点为“已访问”,并记录它在路径的位置 while (!q.isEmpty()) { //开始遍历队列中的顶点 String word = q.poll(); //记录现在正在处理的顶点 int level = map.get(word); //记录现在路径的长度 for (int i = 0; i < word.length(); i++) { char[] wordLetter = word.toCharArray(); for (char j = 'a'; j <= 'z'; j++) { if (wordLetter[i] == j) continue; wordLetter[i] = j; //对于每一位字母,分别替换成另外25个字母 String check = new String(wordLetter); if (check.equals(endWord)) return map.get(word) + 1; //如果已经抵达目标节点,返回当前路径长度+1 if (wordSet.contains(check) && !map.containsKey(check)) { //如果字典中存在邻接节点,且这个邻接节点还未被访问 map.put(check, level + 1); //标记这个邻接节点为已访问,记录其在路径上的位置 q.add(check); //加入队列,以供广度搜索 } } } } return 0; } }


