时间复杂度
一、时间复杂度
分析一下选择、冒泡、插入排序的时间复杂度

时间复杂度:它是用来描述我到底发生了几次常数操作的指标。什么是常数操作?如果某一个操作它跟数据量没有关系,它就是固定时间的,我们管这样的操作叫常数操作。比如1+1和1000000+1000000,1是int,100万也是int的话,这两个过程时间是一样的。因为1是32位的整数,100万也是32位的整数,1+1经历的过程和100万+100万经历的过程一模一样。a+b,如果a和b都是int的话,a和b不管多大,这一步+,它的时间是固定的。我们管+号就是常数时间的操作,它跟数据量没有关系。
同理,+-*/都是这样的。数组寻址也是。arr[]把arr[3]和arr[3000万]这两个位置上的数拿出来时间上是差不多的,固定时间。当你调用一个语句的时候,它可能有些传参,你就记住一点,这个方法执行的这一行语句它是固定时间内能完的呢,还是它是跟数据量有关的?如果它跟数据量有关,它就不是一个常数操作。如果这一句是跟数据量无关的操作,它就是一个固定时间的操作。
冒泡排序,假如数组长度为9,下标是0~8,第一遍是从0~8每两个相邻的数比较最大的数来到8位置上。第二遍,0~7上每两个相邻依次比较,次大的数来到7位置上...它的时间复杂度怎么估算呢?0~1上的数谁大谁往右,(管这个操作叫做a),这个操作a是不是常数时间? 是。
0~8范围,比较交换,操作8次
0~7范围,比较交换,操作7次
0~6范围,比较交换,操作6次
...
等差数列,可以得到一共这么多次,等差数列求和公式:
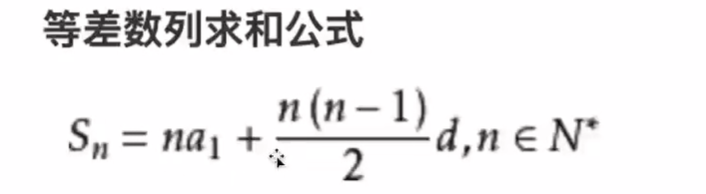
d:公差,上面的冒泡排序,每次操作次数,公差就是1.
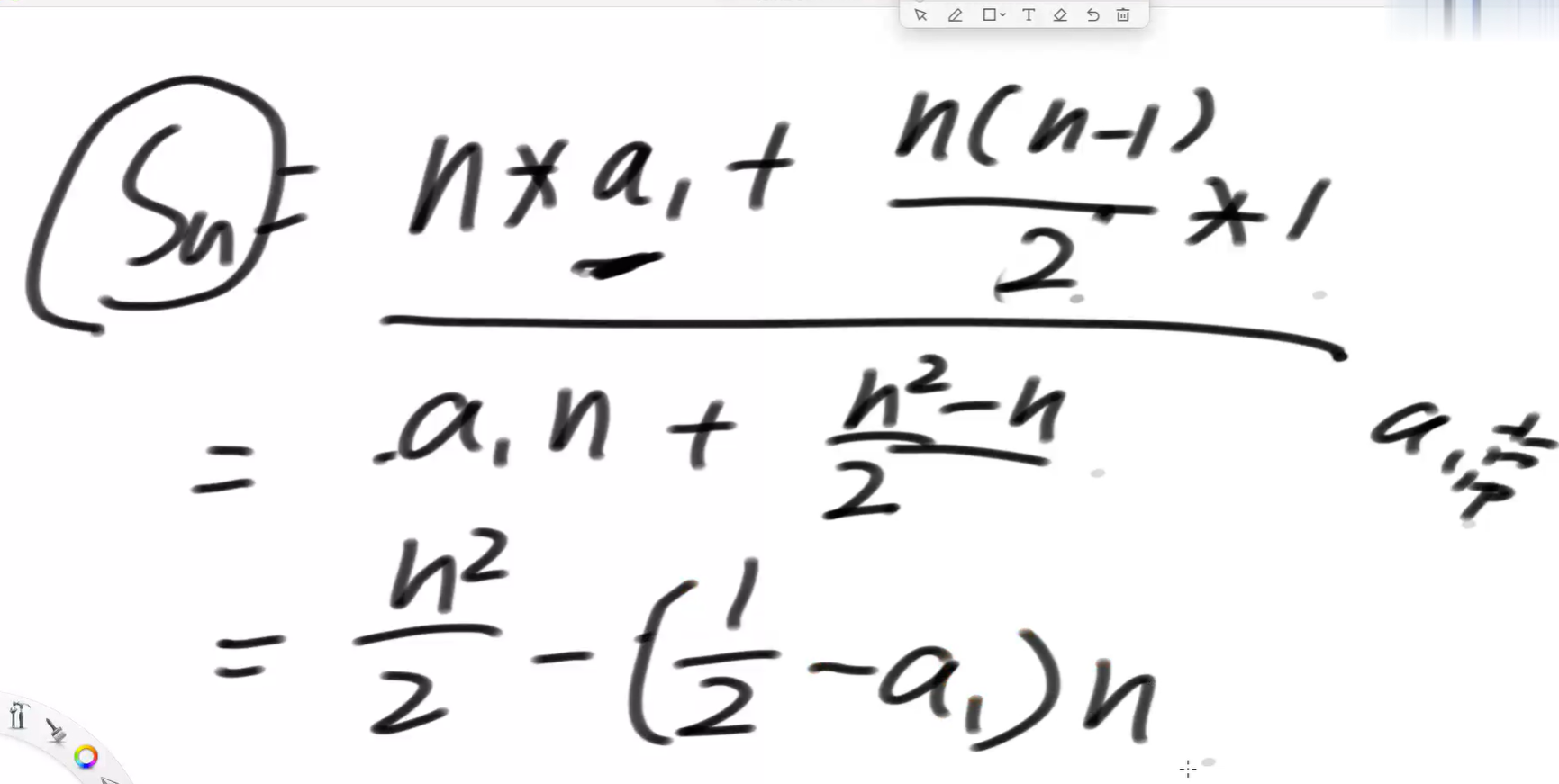
整个表达式中最高阶的东西,就是它的复杂度。o(n²)
复杂度不关心低阶项,它也不关心系数,它只关心最高阶是什么。这就叫时间复杂度。
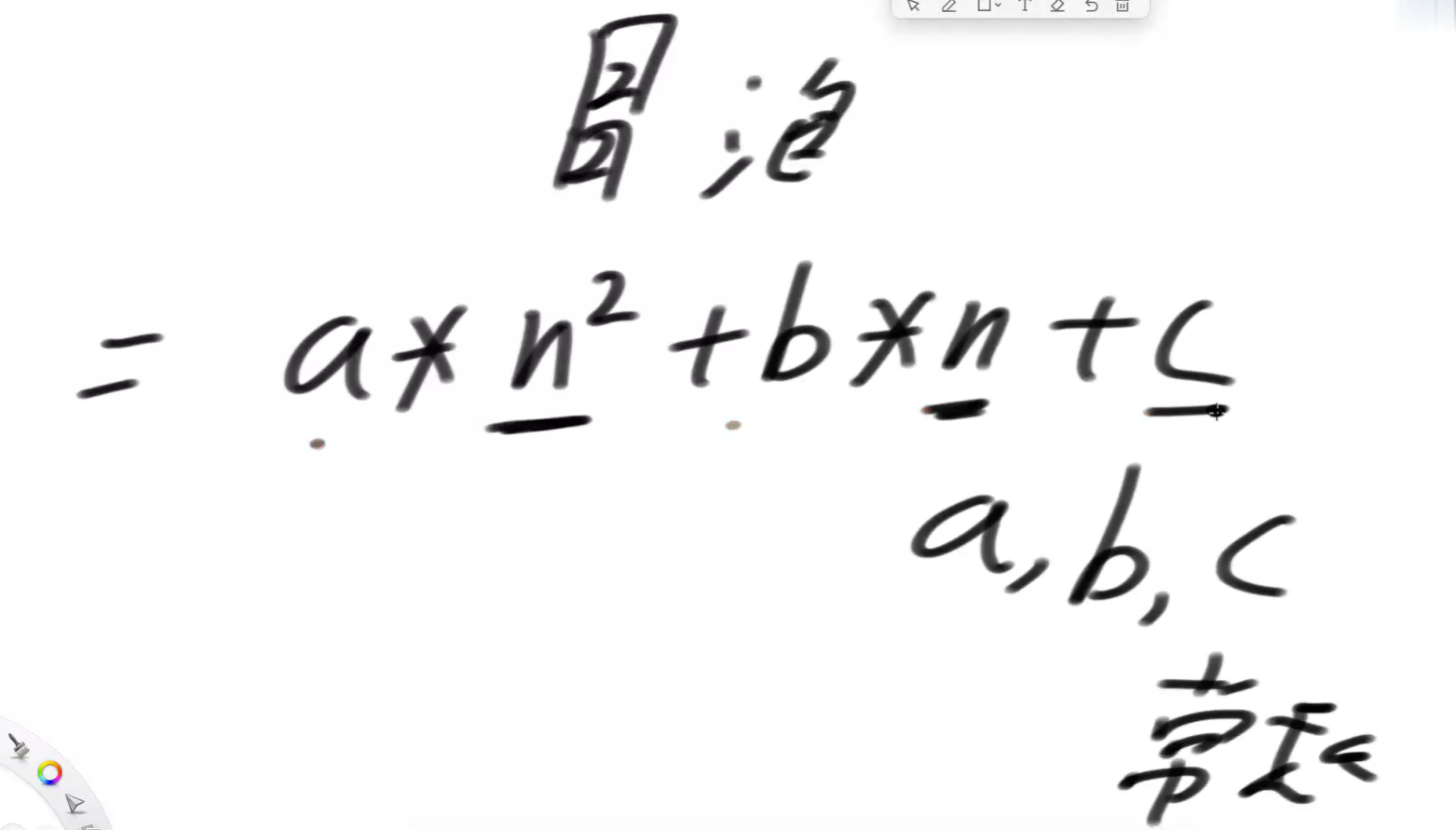
约成n²,o(n²)
时间复杂度是干啥的?为什么做的这么模糊,原因在于它就关心最高阶,当它的数据量很大的时候,它算法运行时间的一个关系。
假如有这两个算法:
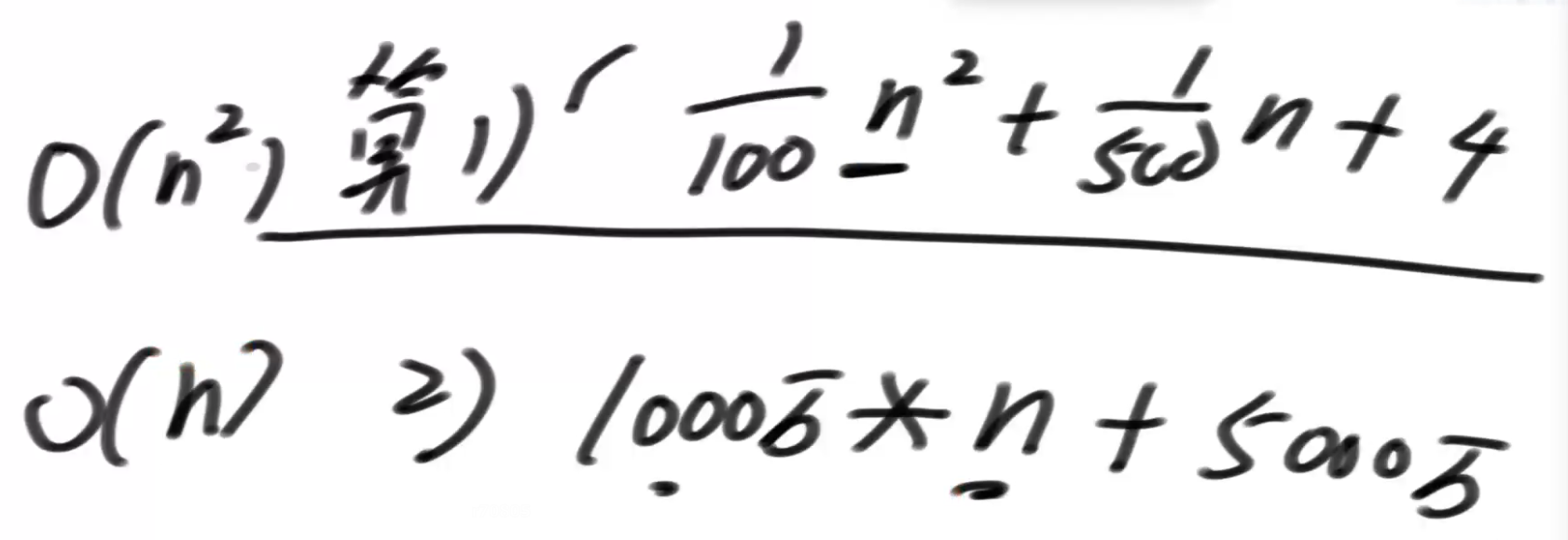
如果n趋近于∞,所有低阶项就变得不重要了。所有系数也变得不重要了。o(n)就是要比o(n²)好。决定这个算法运行时间的就是这个最高阶的次数。时间复杂度好用的地方就在于,数据量很大的情况下,我怎么描述这样一个算法时间的关系。
以后在评估一个算法流程的时候,稍微就可以带一点定性分析的思路,比如估计冒泡排序的时间复杂度:
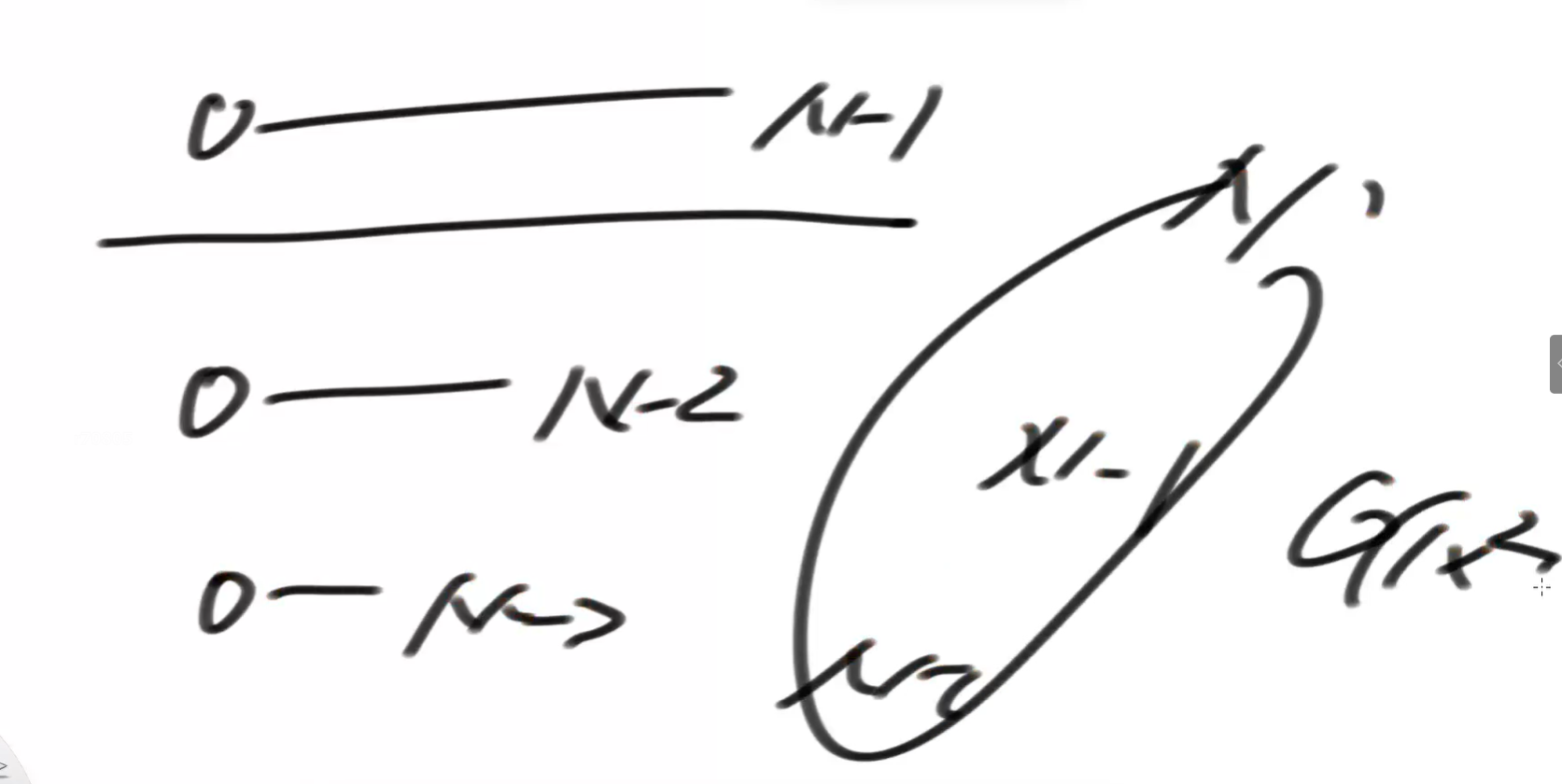
0~N-1,干N件事
0~N-2,干N-1件事
0~N-3,干N-2件事
等差数列,好,时间复杂度就是o(n²)
选择排序:
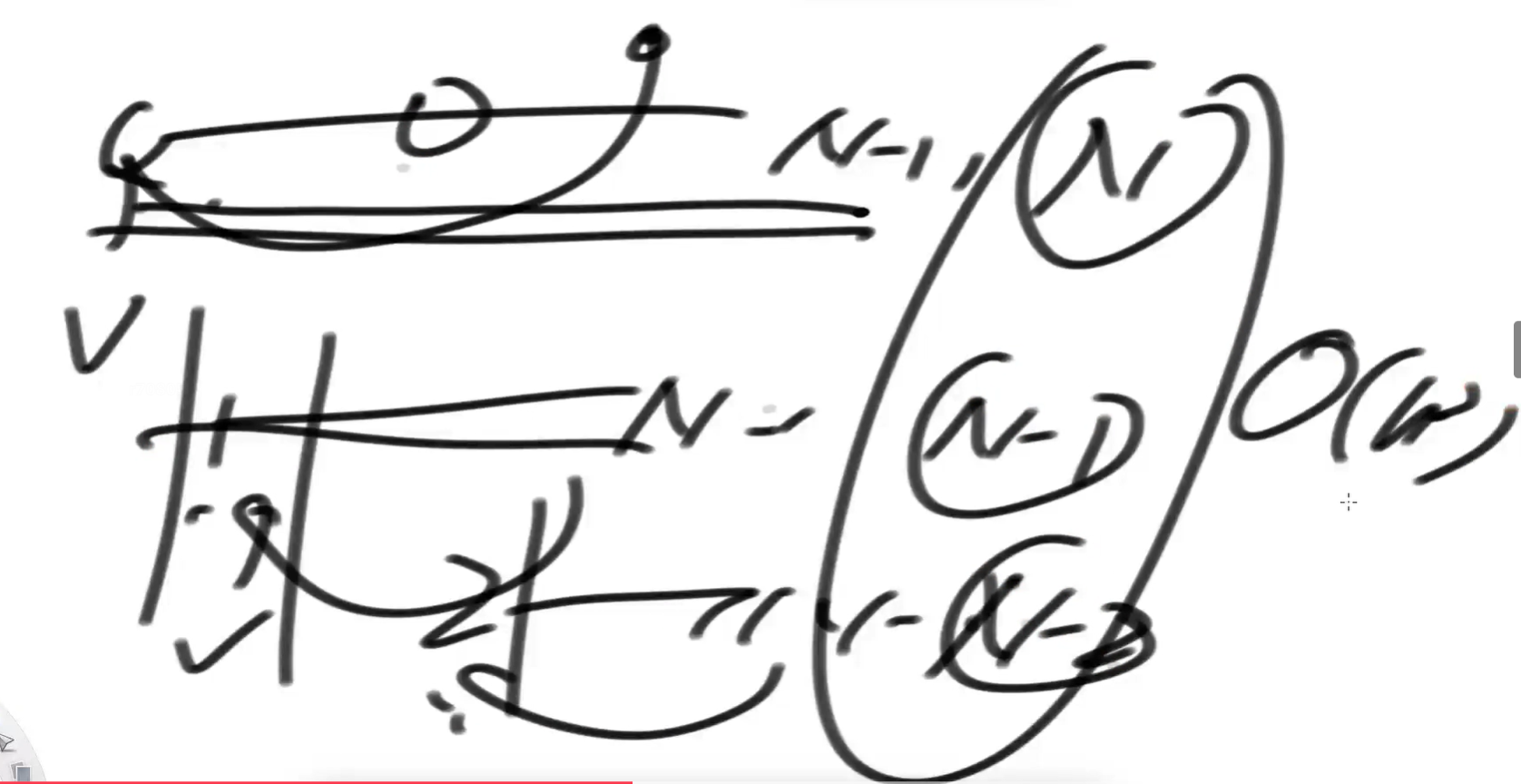
当我知道时间复杂度它会忽略低阶项,跟忽略掉系数,有了这个设定之后,我们在分析一个算法流程的时候,不一定很麻烦,定性的来,只要找到一种等差感,肯定就是n²。
二分法是什么复杂度?
有序数组中找num这件事,o(log2N),这个复杂度比o(N)还要低。

二分法不就是将0~N砍几次能砍完吗?log2N,N = 2 ?次方。?不就是最多砍的次数吗。
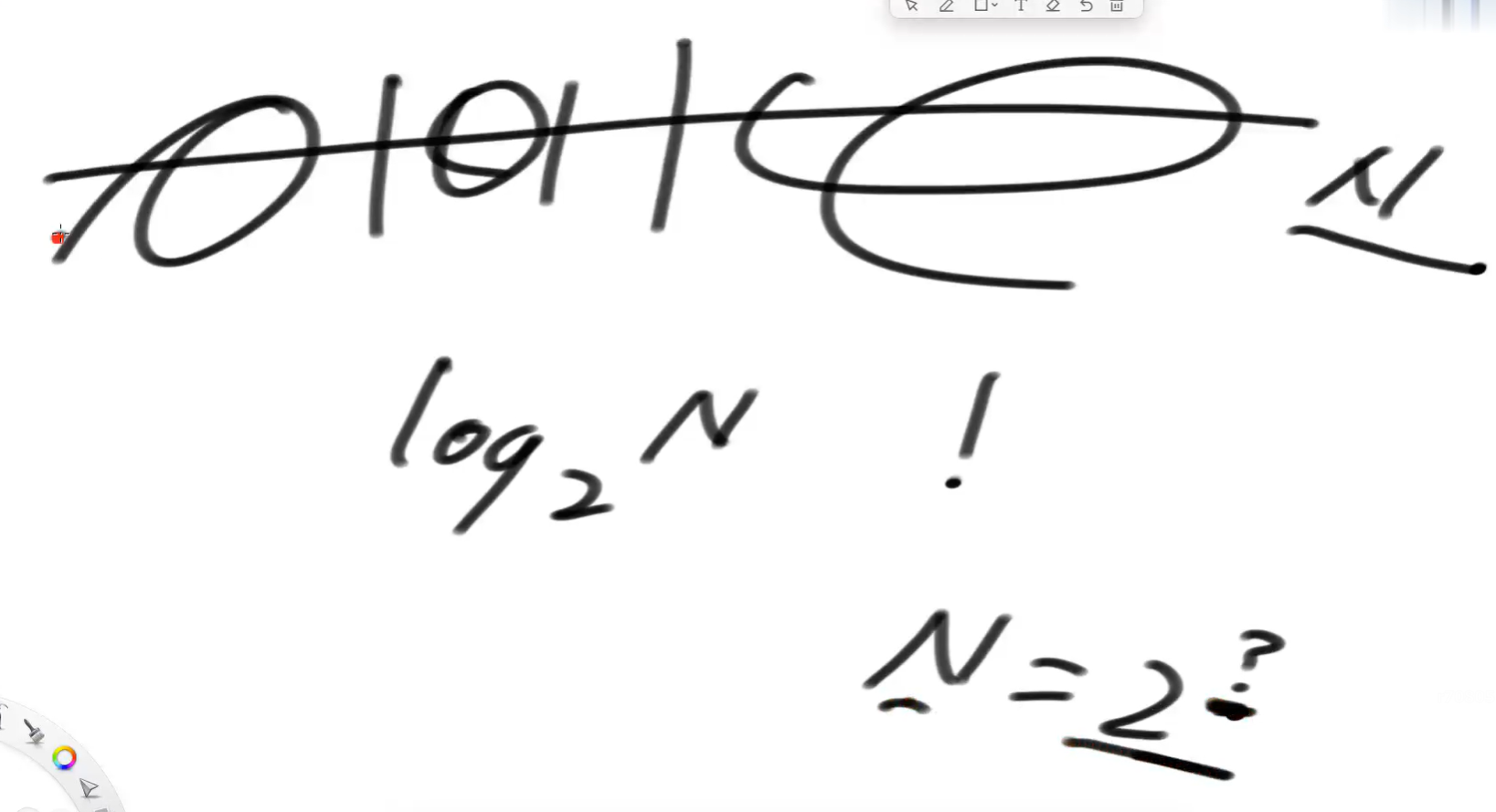
一般情况下就把log2N的以2为底的2省略了,所以当你看到o(logN)的时候,你就默认它是以2为底的。但是log7N,log3N等等都经常忽略这个底,因为这个底只要它比2大,或等于2,出来的结果都会很小,所以就默认写o(logN)了。
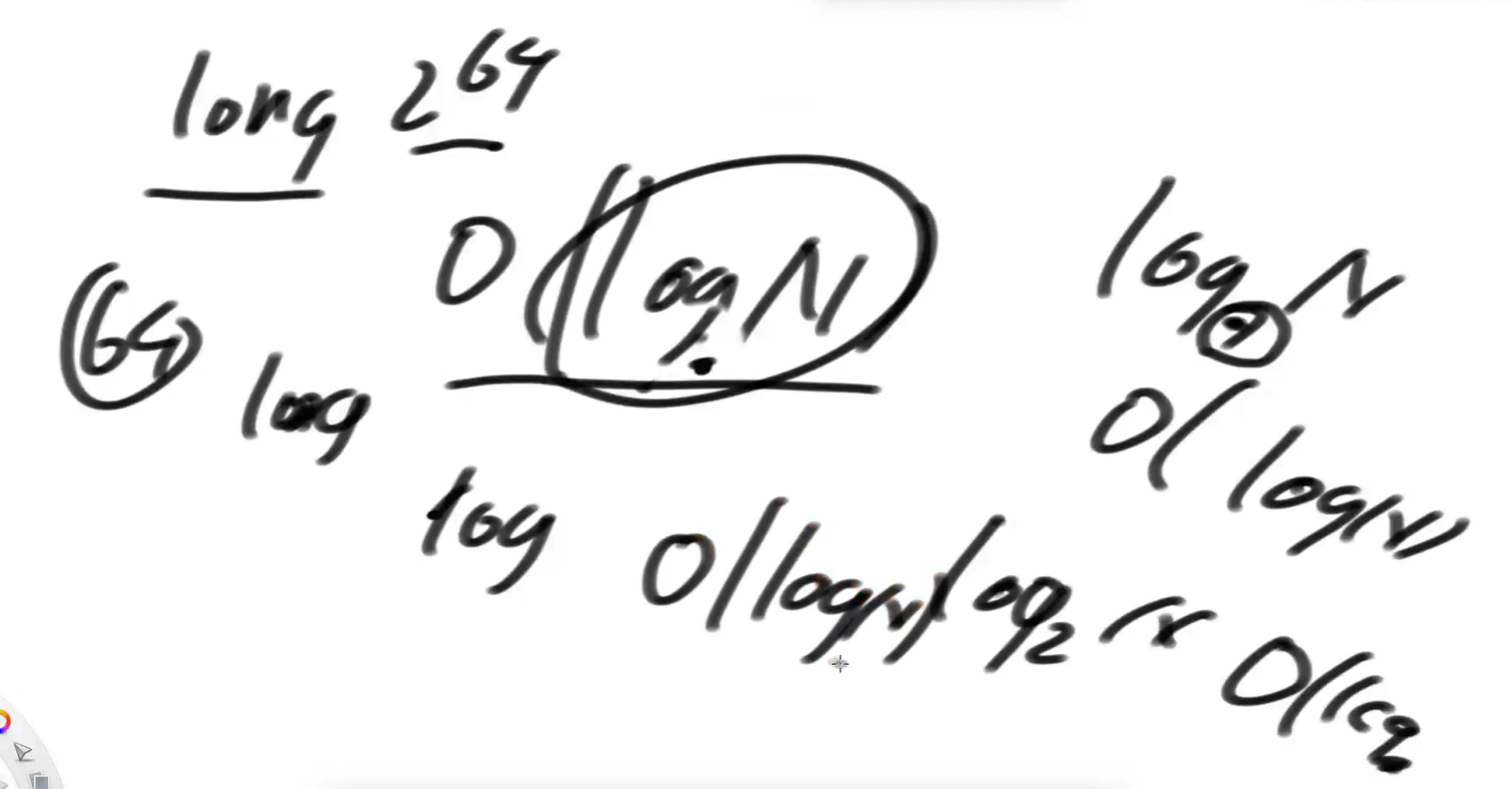
另外,人为规定,常数操作的时间复杂度是o(1),跟数据量无关,是个固定时间的。
另外,算法的时间复杂度在估计的时候,比如你设计出来一个流程,你一定要用最差情况来估计,这个流程最差的情况来估计。不能假设最好的情况来估计。要用最难受的情况来估计这个复杂度和N到底是个什么关系。假设最差情况。
二、常见时间复杂度列表
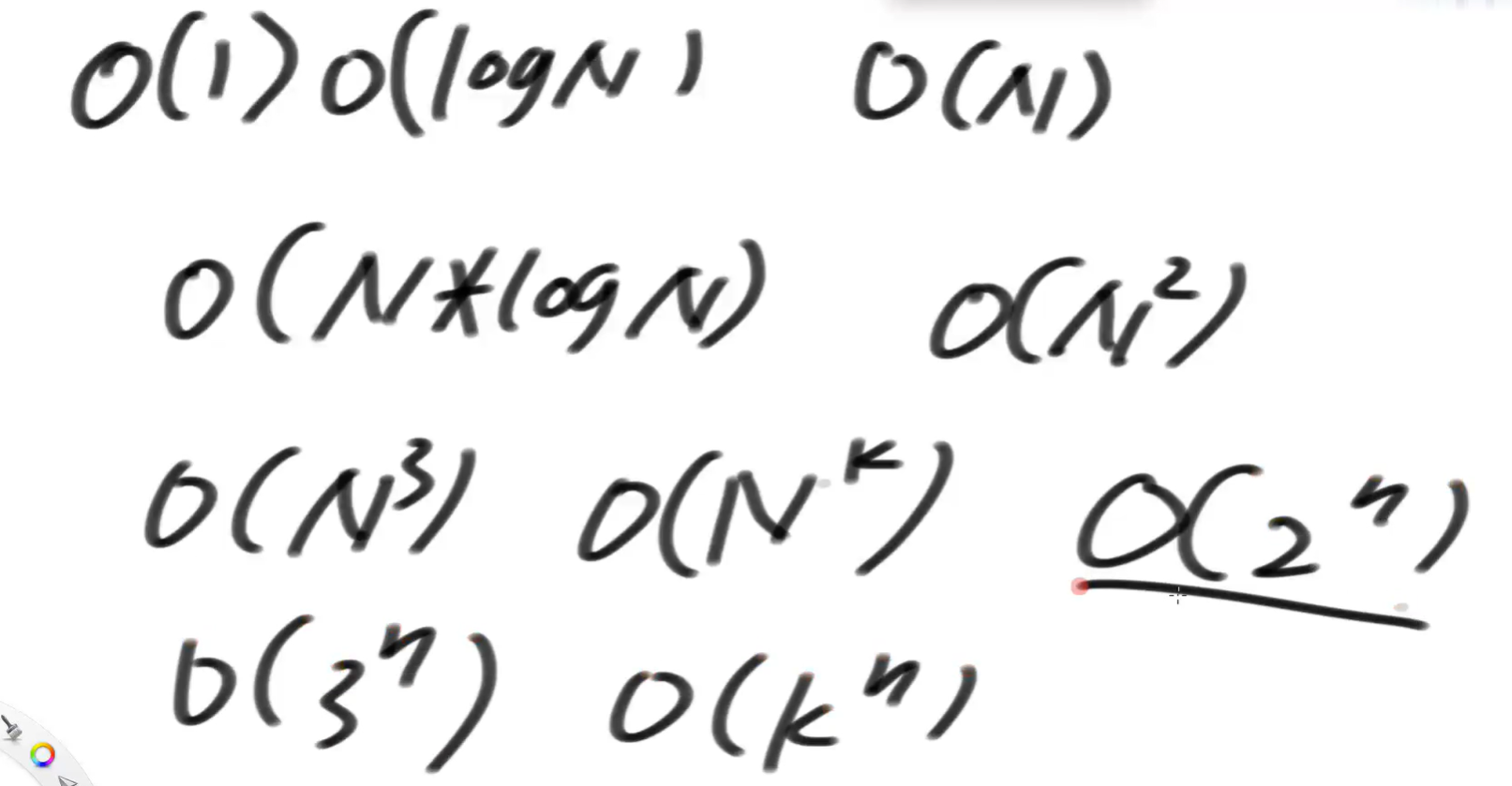
--



 浙公网安备 33010602011771号
浙公网安备 33010602011771号