SVPWM原理分析-基于STM32 MC SDK 5.0
FOC控制的整个过程如下:

论坛和贴子有很多讲理论的,很少实际操作,本文理论联系实际,为大家一步一步揭开SVPWM神秘的面纱。
本文基于ST-FOC 5.4 SVPWM函数分析,力争让读者可以通过这篇文章了解SVPWM的本质:
SVPWM的目的如下:
SVPWM核心思想通过输入的Vα 和Vβ 计算出三相 PWM占空比。
本文的目录如下:
1.任意向量如何通过基本空间矢量合成?任意向量都可以通过相邻的基本空间向量+V0+V7合成。
2.向量扇区的判断?通过(α,β)坐标系下Vα和Vβ值的大小,判断需要合成的向量位于哪个扇区。
3 .基本空间矢量作用时间计算?通过计算(α,β)坐标系下Vα和Vβ值的大小,计算出相邻基本空间矢量作用的时间
4 .占空比计算如何计算?(高电平持续的时间or定时器寄存器的值),根据七段式SVPWM发波原理计算出:hTimePhA ,hTimePhB,hTimePhC的值。
5.总结 SVPWM原理总结。
6.附录。
看一下SVPWM函数原型,输入变量:
|
1 2 3 4 5 6 |
uint16_t PWMC_SetPhaseVoltage( PWMC_Handle_t * pHandle, alphabeta_t Valfa_beta ) typedef struct { int16_t alpha; int16_t beta; } alphabeta_t; |
1.任意向量如何通过基本空间矢量合成?
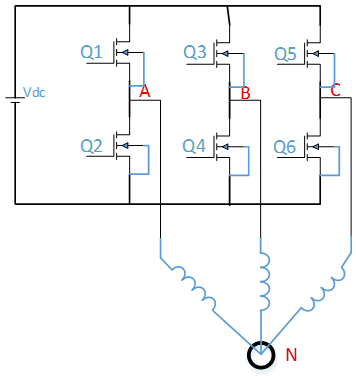
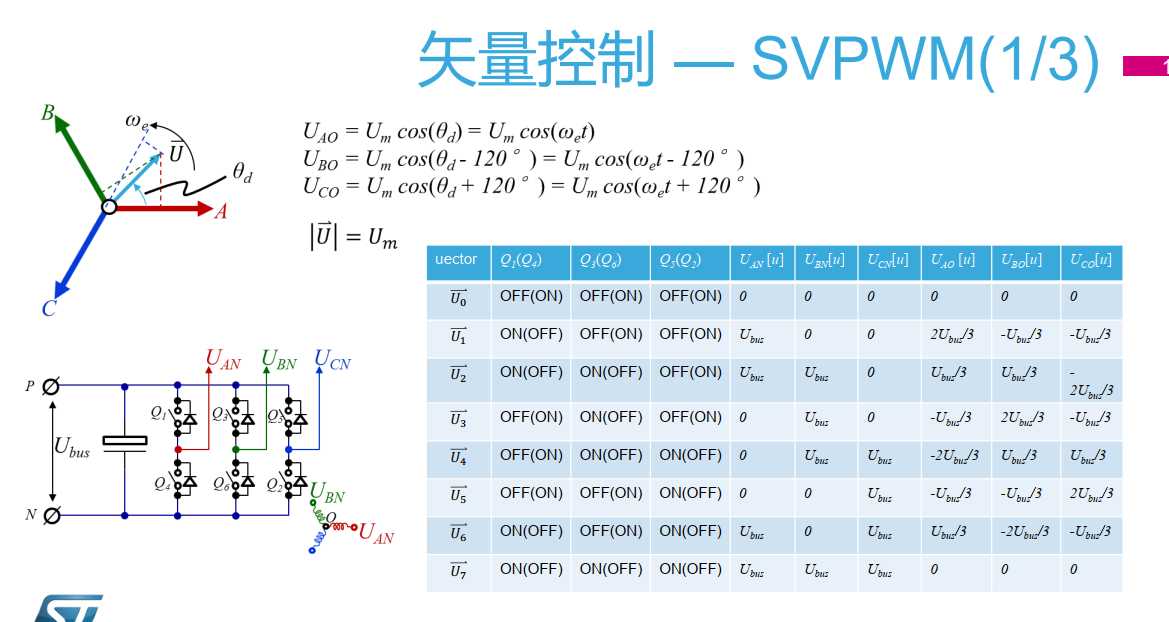
图1 典型三相逆变器拓扑
定义[a,b,c]表示逆变桥上半开关管的状态,当a,b,c为1是表示Q1,Q2,Q3导通,当a,b,c为0时表示Q1,Q2,Q3关闭,且同一桥臂的上管和下管状态相反。根据a,b,C的状态组合,开关管一共有8种状态。如下图所示:
|
序号 |
开关管状态 |
|
|
相电压 |
|
|
线电压 |
|
|
|
|
a |
b |
c |
VAN |
VBN |
VCN |
VAB |
VBC |
VCA |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
-Vdc/3 |
-Vdc/3 |
2Vdc/3 |
0 |
-Vdc |
Vdc |
|
2 |
0 |
1 |
0 |
-Vdc/3 |
2Vdc/3 |
-Vdc/3 |
-Vdc |
Vdc |
0 |
|
4 |
1 |
0 |
0 |
2Vdc/3 |
-Vdc/3 |
-Vdc/3 |
Vdc |
0 |
-Vdc |
|
3 |
0 |
1 |
1 |
-2Vdc/3 |
Vdc/3 |
Vdc/3 |
-Vdc |
0 |
Vdc |
|
5 |
1 |
0 |
1 |
Vdc/3 |
-2Vdc/3 |
Vdc/3 |
Vdc |
-Vdc |
0 |
|
6 |
1 |
1 |
0 |
Vdc/3 |
Vdc/3 |
-2Vdc/3 |
0 |
Vdc |
-Vdc |
|
7 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
表1 开关状态和相电压,线电压的关系
以上分析主要给予KCL和KVL定律,有疑问的小伙伴可以复习一下电路的相关知识。其中有两个零矢量和六个非零矢量,整个空间也被划分为以下六个扇区。应用clark变换(三相-两相变换或者3/2变换,详见《电力拖动自动控制系统-运动控制系统 》第四版 P164),将VAN,VBN,VCN 旋转的坐标系转换到静止的(α,β)坐标系。
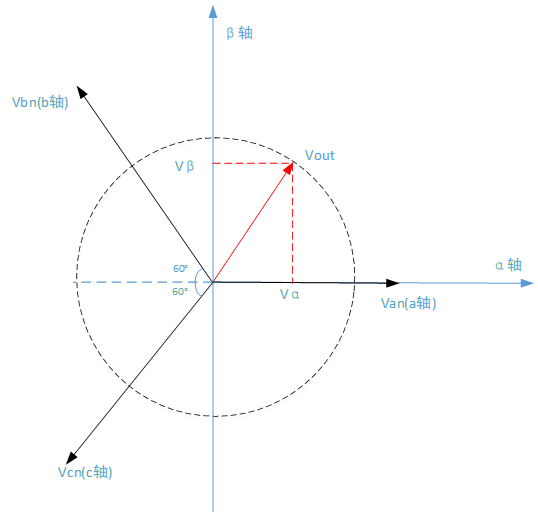
可以得到Vα和Vβ的计算公式:
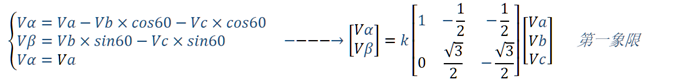
有Va+Vb+Vc=0,Vc=-Va-Vb。
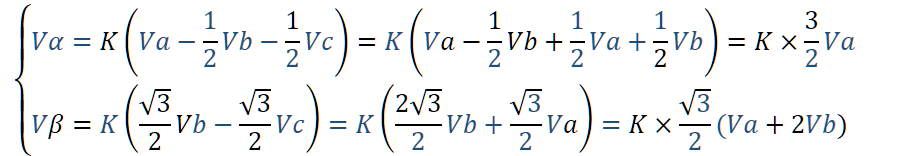
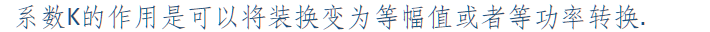
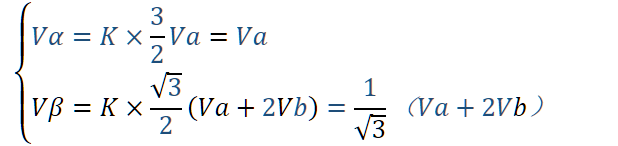
得到计算公式如下:


|
a |
b |
c |
VAN |
VBN |
Vsα |
Vsβ |
Vector |
向量 |
角度 |
二进制 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0[000] |
|
1 |
0 |
0 |
2Vdc/3 |
-Vdc/3 |
2Vdc/3 |
0 |
2Vdc/3 |
V1 |
60 |
4[100] |
|
1 |
1 |
0 |
Vdc/3 |
Vdc/3 |
Vdc/3 |
|
2Vdc/3 |
V2 |
120 |
6[110] |
|
0 |
1 |
0 |
-Vdc/3 |
2Vdc/3 |
-Vdc/3 |
|
2Vdc/3 |
V3 |
180 |
2[010] |
|
0 |
1 |
1 |
-2Vdc/3 |
Vdc/3 |
-2Vdc/3 |
0 |
2Vdc/3 |
V4 |
240 |
3[011] |
|
0 |
0 |
1 |
-Vdc/3 |
-Vdc/3 |
-Vdc/3 |
|
2Vdc/3 |
V5 |
300 |
1[001] |
|
1 |
0 |
1 |
Vdc/3 |
-2Vdc/3 |
Vdc/3 |
|
2Vdc/3 |
V6 |
360 |
5[101] |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
7[111] |
表2 clark变换后基本空间向量的计算【第一象限】
同理我们可以计算(α,β)在第四象限对应的转换关系:
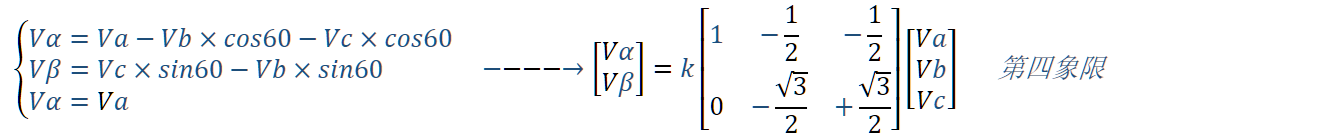
注意以上公式的变化点:
有Va+Vb+Vc=0,Vc=-Va-Vb。
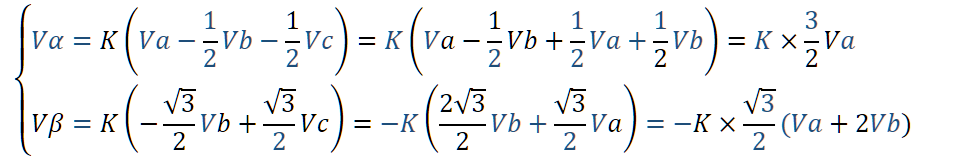
系数K的作用是可以将装换变为等幅值或者等功率转换
在这里我们才管用等幅值变换K=2/3,可以得到:
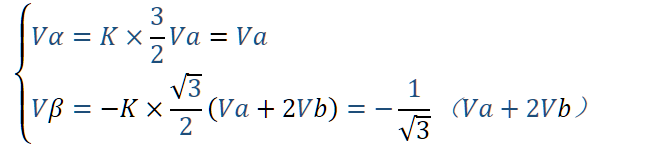
因此可以得到,如下公式:


|
a |
b |
c |
VAN |
VBN |
Vsα |
Vsβ |
Vector |
向量 |
角度 |
二进制 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0[000] |
|
1 |
0 |
0 |
2Vdc/3 |
-Vdc/3 |
2Vdc/3 |
0 |
2Vdc/3 |
V1 |
60 |
4[100] |
|
1 |
1 |
0 |
Vdc/3 |
Vdc/3 |
Vdc/3 |
|
2Vdc/3 |
V2 |
120 |
6[110] |
|
0 |
1 |
0 |
-Vdc/3 |
2Vdc/3 |
-Vdc/3 |
|
2Vdc/3 |
V3 |
180 |
2[010] |
|
0 |
1 |
1 |
-2Vdc/3 |
Vdc/3 |
-2Vdc/3 |
0 |
2Vdc/3 |
V4 |
240 |
3[011] |
|
0 |
0 |
1 |
-Vdc/3 |
-Vdc/3 |
-Vdc/3 |
|
2Vdc/3 |
V5 |
300 |
1[001] |
|
1 |
0 |
1 |
Vdc/3 |
-2Vdc/3 |
Vdc/3 |
|
2Vdc/3 |
V6 |
360 |
5[101] |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
7[111] |
表2 clark变换后基本空间向量的计算【第四象限】
综上所示,以上两种情况得到的基本矢量分布如下:
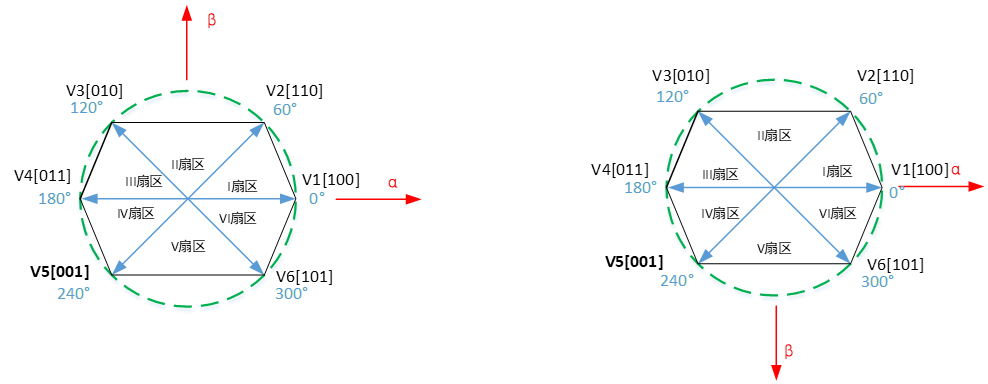
以上可以看到,基本向量的相对位置是没有改变的。
如下图所示:(根据ST-官方教程如下图所示)
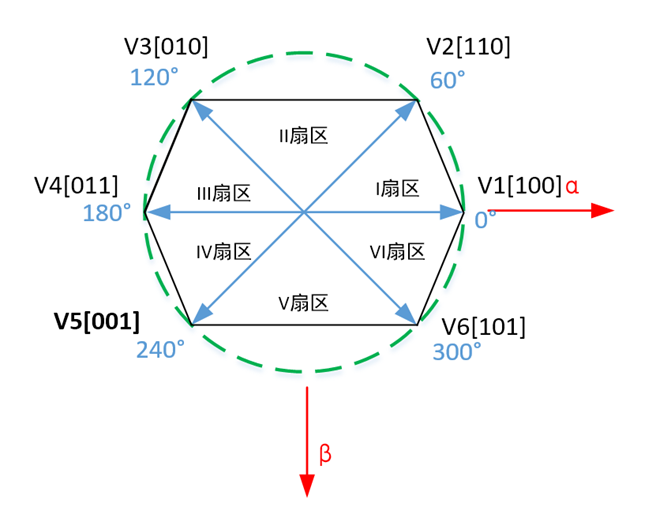
图2 基本空间矢量图
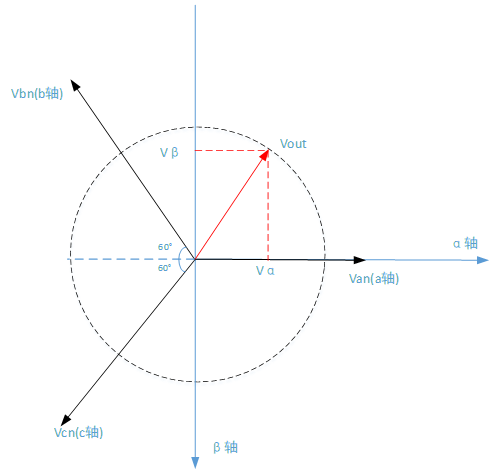
大家要特别关注Vα和Vβ的方向,本文以ST的FOC库为准。

图中2有几个问题比较有意思:
1).为什么矢量的排列顺序是按照4-6-2-3-1-5 或者是4-5-1-3-2-6顺序排列那?这里面值得顺序是二进制开关组合代表的组合。
答案:这六个矢量控制的是功率半导体-Mosfet或者IGBT;这些管子在开关和导通过程中会有热量产生,也就是损耗。为了最大限度的降低损耗,每个扇区(包含扇区内部)的开关切换,都需要保证只改动一个桥臂的动作,这样发热量最小,功率密度才能做更高
2).矢量的排列顺序是4-6-2-3-1-5 或者是4-5-1-3-2-6顺序代表什么意思?
答案:这是电机正反转的区别,假定4-6-2-3-1-5 逆时针为电机正传,则4-5-1-3-2-6表示反转。
备注:不同文档中矢量的名称可能会有改变,这里影响不大,只要调整a,b,c的排列顺序,大家就可以发现其实都一样的,大家看文档的时候不用过于纠结。
SVPWM的目的是为了通过基本的空间的矢量组合得到一个旋转的向量VOUT ,VOUT 可以用(α,β)轴分量Vα和Vβ表示(第四象限)。
2 .扇区的判断
代码如下:
//下面是查找定子电流的扇区号
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
if (wY<0) { if (wZ<0) { bSector = SECTOR_5; } else // wZ >= 0 if (wX<=0) { bSector = SECTOR_4; } else // wX > 0 { bSector = SECTOR_3; } } else // wY > 0 { if (wZ>=0) { bSector = SECTOR_2; } else // wZ < 0 if (wX<=0) { bSector = SECTOR_6; } else // wX > 0 { bSector = SECTOR_1; } } |
VOUT 这个矢量按照我们的设定在圆内依次运行,在每个扇区内VOUT 都是有两个相邻的矢量根据不同的时间合成的矢量,因此第一步我们需要知道VOUT 在哪个扇区。
|
扇区 |
判断条件 |
X(wX) |
Y(wY) |
Z(wZ) |
SECTOR |
|
I |
|
>0 |
>0 |
<0 |
SECTOR_1 |
|
II |
|
>0 |
>0 |
>0 |
SECTOR_2 |
|
III |
|
>0 |
<0 |
>0 |
SECTOR_3 |
|
IV |
|
<0 |
<0 |
>0 |
SECTOR_4 |
|
V |
|
<0 |
<0 |
<0 |
SECTOR_5 |
|
VI |
|
<0 |
>0 |
<0 |
SECTOR_6 |
表3 扇区的判断


设定:X>0则wX=1,否则wX=0.
设定:Y>0则wY=1,否则wY=0.
设定:Z>0则wZ=1,否则wZ=0.
程序中的定义:
|
1 2 3 4 5 6 |
wUAlpha = Stat_Volt_Input.qV_Component1 * T_SQRT3; wUBeta = -(Stat_Volt_Input.qV_Component2 * T);
wX = wUBeta; wY = (wUBeta + wUAlpha)/2; wZ = (wUBeta - wUAlpha)/2; |

图3 基本空间矢量的作用时间计算

以上是理解下面运算的基础。特别需要关注的是,(α,β)轴分量Vα和Vβ表示(第四象限),在第一象限用Vα'和Vβ'表示。
3 .基本空间矢量作用时间计算
知道扇区的位置,接下来计算矢量的作用时间。先讨论一下扇区的发波问题,本文选取7段式SVPWM
关于更多SVPWM的发放方式,详见:https://blog.csdn.net/michaelf/article/details/94013805
采用7段式SVPWM的优点是减少损耗,同时可以较少高次谐波含量,本文不再这里展开,大家了解一种即可
第一扇区计算:
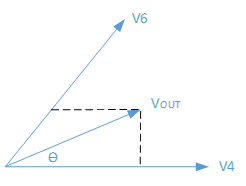
图4 第一扇区基本矢量作用是时间计算
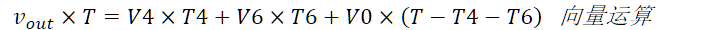
其中T为PWM波形周期,T4是基本矢量V4持续的时间,T6是基本矢量V6持续的时 间。T-T6-T4为V0和V7矢量持续的时间。
将Vout投影到两个相邻的两个矢量V4,V6上,在坐标系α'和β'坐标系下计算,可以得到如下关系:
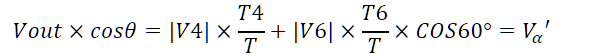

为了后续计算,基本向量归一化处理,步骤如下:
所有的基本空间向量的幅值都是2Vdc/3,当两个零电压矢量作用时间为0时,一个PWM周期内非零电压矢量的作用时间最长,此时的合成空间矢量幅值最大,由下图可以,其幅值最大不会超过图中所示的正六边形边界,而当合成矢量落在该边界之外是,将发生过调试,逆变器输出电压波形将失真。

以上计算得到最大不失真矢量电压为幅值为



图5 基本空间矢量归一化
因此计算:
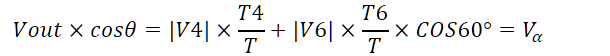


得到 :
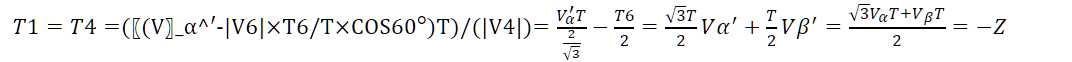
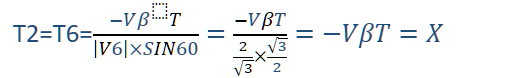
计算结果汇总如下:
扇区 |
N |
T1 |
T2 |
T0+T7 |
I |
3 |
-Z |
X |
T+Z-X |
II |
1 |
Z |
Y |
T-Y-Z |
III |
5 |
X |
-Y |
T-X+Y |
IV |
4 |
-X |
Z |
T+X-Z |
V |
6 |
-Y |
-Z |
T+Y+Z |
VI |
2 |
Y |
-X |
T+X-Y |
表4 基本矢量作用时间计算
详细的计算可以参考一下链接:https://blog.csdn.net/michaelf/article/details/94013805
需要关注两点,一个是Vβ的方向,一个是基本矢量的归一化。
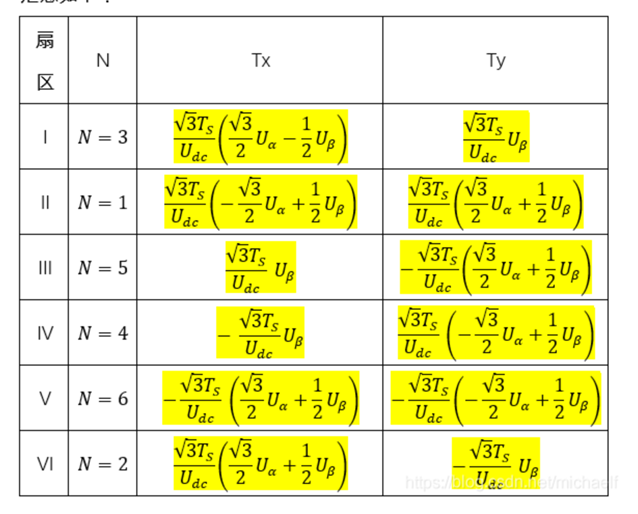
表5基本矢量作用时间计算。
4 .占空比计算(高电平持续的时间or定时器寄存器的值)
根据3分析,我们可以计算出合成向量在不同的扇区,相邻矢量作用的时间及 V0和V7作用的时间。
向上代码,后分析:
FOC 5.0代码分析如下:
|
1 2 3 4 5 6 7 8 9 |
uint16_t PWMperiod; /**< PWM period expressed in timer clock cycles unit: * @f$hPWMPeriod = TimerFreq_{CLK} / F_{PWM}@f$ */ #define PWM_PERIOD_CYCLES (uint16_t)(ADV_TIM_CLK_MHz*\ (unsigned long long)1000000u/((uint16_t)(PWM_FREQUENCY)))
#define ADV_TIM_CLK_MHz 72 #define PWM_FREQUENCY 16000
PWM_Handle_M1.PWMperiod = PWM_PERIOD_CYCLES,
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92
|
__weak uint16_t PWMC_SetPhaseVoltage( PWMC_Handle_t * pHandle, alphabeta_t Valfa_beta ) { int32_t wX, wY, wZ, wUAlpha, wUBeta, wTimePhA, wTimePhB, wTimePhC;
wUAlpha = Valfa_beta.alpha * ( int32_t )pHandle->hT_Sqrt3; wUBeta = -( Valfa_beta.beta * ( int32_t )( pHandle->PWMperiod ) ) * 2;
wX = wUBeta; wY = ( wUBeta + wUAlpha ) / 2; wZ = ( wUBeta - wUAlpha ) / 2;
/* Sector calculation from wX, wY, wZ */ if ( wY < 0 ) { if ( wZ < 0 ) { pHandle->Sector = SECTOR_5; wTimePhA = ( int32_t )( pHandle->PWMperiod ) / 4 + ( ( wY - wZ ) / ( int32_t )262144 ); wTimePhB = wTimePhA + wZ / 131072; wTimePhC = wTimePhA - wY / 131072; pHandle->lowDuty = wTimePhC; pHandle->midDuty = wTimePhA; pHandle->highDuty = wTimePhB; } else /* wZ >= 0 */ if ( wX <= 0 ) { pHandle->Sector = SECTOR_4; wTimePhA = ( int32_t )( pHandle->PWMperiod ) / 4 + ( ( wX - wZ ) / ( int32_t )262144 ); wTimePhB = wTimePhA + wZ / 131072; wTimePhC = wTimePhB - wX / 131072; pHandle->lowDuty = wTimePhC; pHandle->midDuty = wTimePhB; pHandle->highDuty = wTimePhA; } else /* wX > 0 */ { pHandle->Sector = SECTOR_3; wTimePhA = ( int32_t )( pHandle->PWMperiod ) / 4 + ( ( wY - wX ) / ( int32_t )262144 ); wTimePhC = wTimePhA - wY / 131072; wTimePhB = wTimePhC + wX / 131072; pHandle->lowDuty = wTimePhB; pHandle->midDuty = wTimePhC; pHandle->highDuty = wTimePhA; } } else /* wY > 0 */ { if ( wZ >= 0 ) { pHandle->Sector = SECTOR_2; wTimePhA = ( int32_t )( pHandle->PWMperiod ) / 4 + ( ( wY - wZ ) / ( int32_t )262144 ); wTimePhB = wTimePhA + wZ / 131072; wTimePhC = wTimePhA - wY / 131072; pHandle->lowDuty = wTimePhB; pHandle->midDuty = wTimePhA; pHandle->highDuty = wTimePhC; } else /* wZ < 0 */ if ( wX <= 0 ) { pHandle->Sector = SECTOR_6; wTimePhA = ( int32_t )( pHandle->PWMperiod ) / 4 + ( ( wY - wX ) / ( int32_t )262144 ); wTimePhC = wTimePhA - wY / 131072; wTimePhB = wTimePhC + wX / 131072; pHandle->lowDuty = wTimePhA; pHandle->midDuty = wTimePhC; pHandle->highDuty = wTimePhB; } else /* wX > 0 */ { pHandle->Sector = SECTOR_1; wTimePhA = ( int32_t )( pHandle->PWMperiod ) / 4 + ( ( wX - wZ ) / ( int32_t )262144 ); wTimePhB = wTimePhA + wZ / 131072; wTimePhC = wTimePhB - wX / 131072; pHandle->lowDuty = wTimePhA; pHandle->midDuty = wTimePhB; pHandle->highDuty = wTimePhC; } }
pHandle->CntPhA = ( uint16_t )wTimePhA; pHandle->CntPhB = ( uint16_t )wTimePhB; pHandle->CntPhC = ( uint16_t )wTimePhC;
return ( pHandle->pFctSetADCSampPointSectX( pHandle ) ); } |
先看第一扇区七段式SVPWM的顺序是:0-4-6-7-6-4-0.重点V0和V7的作用时间相等。很重要。

扇区切换时间如下:X=1,Y=2
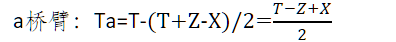
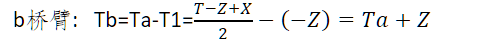
c桥臂: Tc=Tb-T2=Tb-X
同理可以推算出其他各个扇区的切换时间,汇总各个扇区的切换时间,对应关系如下:
|
扇区 |
I |
II |
III |
IV |
V |
VI |
备注 |
|
N |
3 |
1 |
5 |
4 |
6 |
2 |
程序对应的名称 |
|
Ta |
|
|
|
|
|
|
hTimePhA |
|
Tb |
|
|
|
|
|
|
hTimePhB |
|
Tc |
Tb-X |
Tb-Y |
Tb-Y |
Tb-X |
Tb-Y |
Tb-Y |
hTimePhC |
表6 个桥臂作用时间计算
以上内容是结构ST的SVPWM教材分析,ST官方教程使用3页PPT标识,详细推到过程如以上所示。
结合代码,我们会发现几个问题点,
1) 为什么要除以4? pHandle->PWMperiod / 4
前面wUBeta 和wUAlpha 计算式PWMperiod *2,因此在这里需要除去2.实际结果是T/2.
参考PWM定时器配置:
|
1 2 3 4 5 6
|
htim1.Instance = TIM1;//设置频率为16k htim1.Init.Prescaler = ((TIM_CLOCK_DIVIDER) - 1);//分频系数为0 htim1.Init.CounterMode = TIM_COUNTERMODE_CENTERALIGNED1;//TIM中央对齐模式1计数模式 htim1.Init.Period = ((PWM_PERIOD_CYCLES) / 2);/*Period max 4500 设置了在下一个更新事件装入活动的自动重装载寄存器周期的值。value:0x0000~0xFFFF*/ htim1.Init.ClockDivision = TIM_CLOCKDIVISION_DIV2;/*设置定时器时钟CK_INT频率与死区发生器以及数字滤波器采样时钟频率分频化。Value:*/ htim1.Init.RepetitionCounter = REP_RATE;/*是否使用重复定时器,当该值不为0的时候,计数器计数值达到周期数时,该值减1,计数器重新计数,当该值减到0的时候才会产生事件。*/ htim1.Init.AutoReloadPreload = TIM_AUTORELOAD_PRELOAD_DISABLE; |
正好配置TIM1为中央对齐模式1(TIM_COUNTERMODE_CENTERALIGNED1),在上面代码的配置中,载波周期为16KHz,Period(ARR)=4500,CH1的CntPhA (CCR)=800。采用的PWM1模式,
即CNT小于CCR时,输出有效电平,大于CCR小于ARR时,输出无效电平,又配置CHx的有效电平为高电平,CHxN的有效电平为高电平,则可以得到下面的PWM波形:
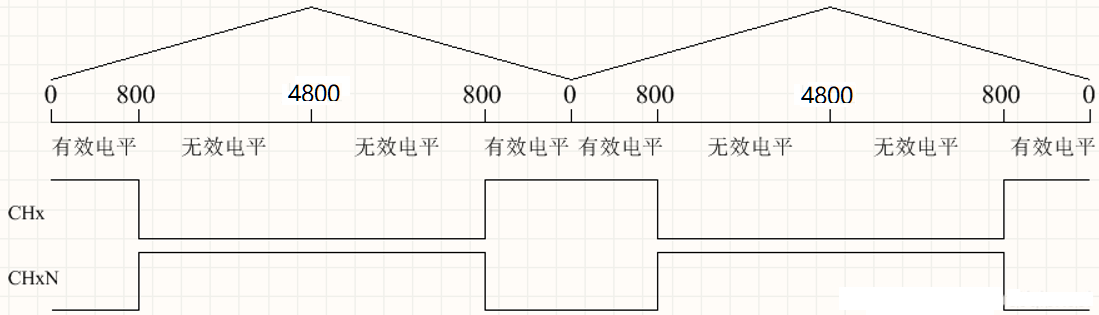
如果CHxN的有效电平是低电平,则输出的CHx和CHxN的波形是相同的。(可能CHx和CHxN有效电平的叫法相反)
从以上可T=(PWM_PERIOD_CYCLES) / 2.,PWM_PERIOD_CYCLES=2T.
2)为什么要除以131072?((((T + wX) - wZ)/2)/131072)


Q15,电流采用了Q15表示(左对齐),2^15 = 32768
3)为什么要除以262144 ?( ( wX - wZ ) / ( int32_t )262144 );
同问题2,262144 =32768X4=Q15*4.
5.总结
6.补充内容,PPT截图如下:





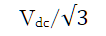
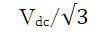


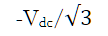

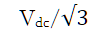

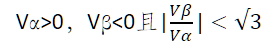

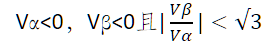
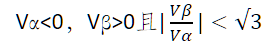
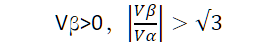
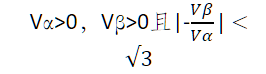

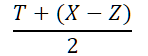
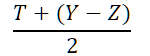
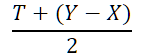
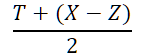

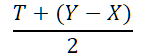


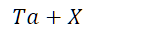
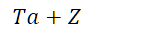


 浙公网安备 33010602011771号
浙公网安备 33010602011771号