树-森林、树、二叉树的转换

一、概念

　　由于二叉树是一种比较确定的数据结构，因此操作它比较简单，但是由于一般树的结构并不固定，因此操作起来非常麻烦，我们可以将一般树转换成二叉树，以二叉树的形式来存储一般树，当程序需要一般树时，再将二叉树转换成一般树。

　　森林：如果将一颗一般树的根节点去掉，这棵树就变成了森林，其实森林就是有多个根节点的树。

 

二、树的转换：

　　a、多叉树向二叉树转换的方法：

　　1、加虚线：同一个父节点的相邻兄弟节点之间的虚线

　　 2、抹实线：每节点只保留它与最左子节点的连线，与其他子节点的连线被抹掉。

　　3、虚改实：虚线改成实线

 

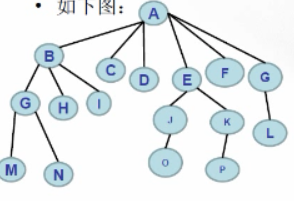
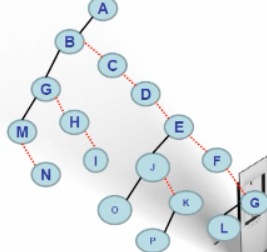
 结论：

　　红虚线就是新增的父子关系，因此多叉树转换成二叉树的关键思路就是：所有子节点只保留左节点，其他子节点转为左节点的右子节点链。

 

　　b、因此森林也可以转换为二叉树：

　　森林如下：

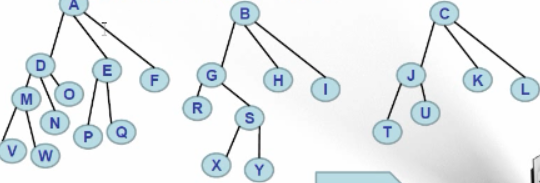
转换成的二叉树为：

　　

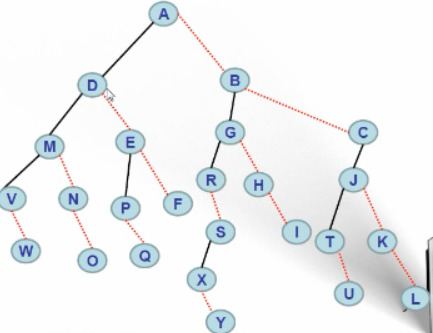
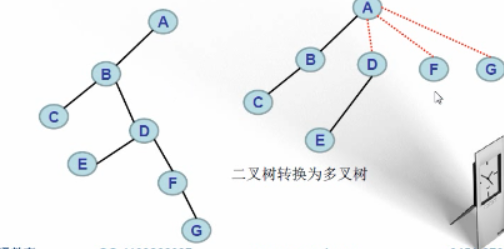
　　c、二叉树转换为多叉树

　　　　1、加虚线：若某节点I是父节点的左子节点，则将该节点I的右孩子链的所有节点分别与节点I的父节点添加连线

　　　　2、抹线：把有虚线的节点与原父节点的连线抹去

　　　　3、整理：虚改实，并按层排列

 

　　d、二叉树转换成森林

　　　　如果二叉树的根节点有右子节点-右子节点就代表是根节点的兄弟节点，这种情况会转换得到森林。

　　　　如果二叉树的根节点的右子节点链只有一个节点，那么转换出来的森林将只有两棵树；如果二叉树的根节点的右子节点链有N个节点，那么转换出来的森林就有N+1棵树。