　　A write-release is most often used in a producer scenario，performs two consecutive writes (e.g., writing to g_data and then g_ready), and we need to ensure that all other threads will see the two writes in the correct order. We can enforce this ordering by making the second of these two writes a write-release.

　　A read-acquire is typically used in a consumer scenario—in which a thread performs two consecutive reads in which the second is conditional on the first (e.g., only reading g_data after a read of the flag g_ready comes back true). We enforce this ordering by making sure that the first read is a read-acquire.

int32_t g_data = 0;
int32_t g_ready = 0;
void ProducerThread() // running on Core 1
{
    g_data = 42;
    
    // make the write to g_ready into a write-release
    // by placing a release fence *before* it
    RELEASE_FENCE();
    
    g_ready = 1;
}
void ConsumerThread() // running on Core 2
{
    // make the read of g_ready into a read-acquire
    // by placing an acquire fence *after* it
    while (!g_ready)
        PAUSE();
    
    ACQUIRE_FENCE();
    
    // we can now read g_data safely...
    ASSERT(g_data == 42);
}

View Code

6、CPU Memory Models

　　the DEC Alpha has notoriously weak semantics by default, requiring careful fencing in almost all situations. At the other end of the spectrum, an Intel x86 CPU has quite strong memory ordering semantics by default.

7、Fence Instructions on Real CPUs

　　The Intel x86 ISA specifies three fence instructions: sfence provides release semantics, lfence provides acquire semantics, and mfence acts as a full fence.

　　Certain x86 instructions may also be prefixed by a lock modifier to make them behave atomically, and to provide a memory fence prior to execution of the instruction.

　　The x86 ISA is strongly ordered by default, meaning that fences aren’t actually required in many cases where they would be on CPUs with weaker default ordering semantics.　　

8、Atomic Variables

　　C++11, the class template std::atomic<T> allows virtually any data type to be converted into an atomic variable. Using these facilities, our producer-consumer example can be written as follows:

　　the std::atomic family of templates provides its variables with “full fence” memory ordering semantics by default (although weaker semantics can be specified if desired). This frees us to write lock-free code without having to worry about any of the three causes of data race bugs.

std::atomic<float> g_data;
std::atomic_flag g_ready = false;

void ProducerThread()
{
    // produce some data
    g_data = 42;
    
    // inform the consumer
    g_ready = true;
}

void ConsumerThread()
{
    // wait for the data to be ready
    while (!g_ready)
        PAUSE();
        
    // consume the data
    ASSERT(g_data == 42);
}

View Code

　　atomic<> 变量，不仅仅保证了原子，也保证了 compiler、cpu、memory order 导致的bug。

　　the implementations of std::atomic<T> and std:: atomic_flag are, of course, complex. The standard C++ library has to be portable, so its implementation makes use of whichever atomic and barrier machine language instructions happen to be available on the target platform.

　　atomic<> 根据 target platform 的不同，而被编译成不同的 ML instruction。

　　atomic<T>。当T很小时（32/64位以下），atomic 采用 atomic instruction；当 T 很大时（32/64位以上），atomic 采用 mutex。You can call is_lock_free() on any atomic variable to find out whether its implementation really is lock-free on

your target hardware.

9、C++ Memory Order

　　By default, C++ atomic variables make use of full memory barriers, to ensure that they will work correctly in all possible use cases. However, it is possible to relax these guarantees, by passing a memory order semantic.

　　1） Relaxed. guarantees only atomicity. No barrier or fence is used.

　　2）Consume. no other read or write within the same thread can be reordered before this read. In other words, this semantic only serves to prevent compiler optimizations and out-of-order execution from reordering the instructions—it does nothing to ensure any particular memory ordering semantics within the cache coherency domain.

　　　　　　　　类似于 acquire，但不负责 memory-order 问题。（acquire负责）

　　3）Release. A write performed with release semantics guarantees that no other read or write in this thread can be reordered after it, and the write is guaranteed to be visible by other threads reading the same address. Itemploys a release fence in the CPU’s cache coherency domain to accomplish this.

　　　　　　　　等同于 Release semantics。

　　4）Acquire.

　　　　　　　　完全等同于 acquire。

　　5）Acquire/Release. full memory fence.

　　Using these memory order specifiers requires switching from std:: atomic’s overloaded assignment and cast operators to explicit calls to store() and load().

std::atomic<float> g_data;
std::atomic<bool> g_ready = false;

void ProducerThread()
{
    // produce some data
    g_data.store(42, std::memory_order_relaxed);
    
    // inform the consumer
    g_ready.store(true, std::memory_order_release);
}

void ConsumerThread()
{
    // wait for the data to be ready
    while (!g_ready.load(std::memory_order_acquire))
    PAUSE();
    
    // consume the data
    ASSERT(g_data.load(std::memory_order_relaxed) == 42);
}

View Code

10、Concurrency in Interpreted Programming Languages

　　C++ compile or assemble down to raw machine code that is executed directly by the CPU. As such, atomic operations and locks must be implemented with the aid of special machine language instructions that provide atomic operations and cache coherent memory barriers, with additional help from the kernel (which makes sure threads are put to sleep and awoken appropriately) and the compiler (which respects barrier instructions when optimizing the code).

　　In C/C++ a volatile variable is not atomic. However, in Java and C#, the volatile type qualifier does guarantee atomicity.

11、Basic Spin Lock

　　std::memory_order_acquire：保证后面的读不会发生在本次读的前面。

　　std::memory_order_release：保证所有前面的写都已完成。

class SpinLock
{
    std::atomic_flag m_atomic;
    public:
    SpinLock() : m_atomic(false) { }
    
    bool TryAcquire()
    {
        // use an acquire fence to ensure all subsequent
        // reads by this thread will be valid
        bool alreadyLocked = m_atomic.test_and_set(std::memory_order_acquire);
        return !alreadyLocked;
    }
    
    void Acquire()
    {
        // spin until successful acquire
        while (!TryAcquire())
        {
            // reduce power consumption on Intel CPUs
            // (can substitute with std::this_thread::yield()
            // on platforms that don't support CPU pause, if
            // thread contention is expected to be high)
            PAUSE();
        }
    }
    
    void Release()
    {
        // use release semantics to ensure that all prior
        // writes have been fully committed before we unlock
        m_atomic.clear(std::memory_order_release);
    }
};

View Code

12、Scoped Locks

　　类似智能指针。自动给 lock 加锁、解锁。

13、Reentrant Locks

　　We can relax this reentrancy restriction if we can arrange for our spin lock class to cache the id of the thread that has locked it.

class ReentrantLock32
{
    std::atomic<std::size_t> m_atomic;
    std::int32_t m_refCount;
    
public:
    ReentrantLock32() : m_atomic(0), m_refCount(0) { }
    
    void Acquire()
    {
        std::hash<std::thread::id> hasher;
        std::size_t tid = hasher(std::this_thread::get_id());
        
        // if this thread doesn't already hold the lock...
        if (m_atomic.load(std::memory_order_relaxed) != tid)
        {
            // ... spin wait until we do hold it
            std::size_t unlockValue = 0;
            while (!m_atomic.compare_exchange_weak(
                                unlockValue,
                                tid,
                                std::memory_order_relaxed, // fence below!
                                std::memory_order_relaxed))
            {
                unlockValue = 0;
                PAUSE();
            }
        }
        
        // increment reference count so we can verify that
        // Acquire() and Release() are called in pairs
        ++m_refCount;
        
        // use an acquire fence to ensure all subsequent
        // reads by this thread will be valid
        std::atomic_thread_fence(std::memory_order_acquire);
    }

    void Release()
    {
        // use release semantics to ensure that all prior
        // writes have been fully committed before we unlock
        std::atomic_thread_fence(std::memory_order_release);
        
        std::hash<std::thread::id> hasher;
        std::size_t tid = hasher(std::this_thread::get_id());
        std::size_t actual = m_atomic.load(std::memory_order_relaxed);
        assert(actual == tid);
        
        --m_refCount;

        if (m_refCount == 0)
        {
            // release lock, which is safe because we own it
            m_atomic.store(0, std::memory_order_relaxed);
        }
    }

    bool TryAcquire()
    {
        std::hash<std::thread::id> hasher;
        std::size_t tid = hasher(std::this_thread::get_id());
        bool acquired = false;
        if (m_atomic.load(std::memory_order_relaxed) == tid)
        {
            acquired = true;
        }
        else
        {
            std::size_t unlockValue = 0;
            acquired = m_atomic.compare_exchange_strong(
            unlockValue,
            tid,
            std::memory_order_relaxed, // fence below!
            std::memory_order_relaxed);
        }
        if (acquired)
        {
            ++m_refCount;
            std::atomic_thread_fence(std::memory_order_acquire);
        }
        
        return acquired;
    }
    
};

View Code

14、Readers-Writer Locks

　　Whenever a writer thread attempts to acquire the lock, it should wait until all readers are finished.

　　we’ll store a reference count indicating how many readers currently hold the lock.

　　A readers-writer lock suffers from starvation problems: A writer that holds the lock too long can cause all of the readers to starve, and likewise a lot of readers can cause the writers to starve.

15、Lock-Not-Needed Assertions

　　通过 Assert 来 Check 多个线程是否会互相 overlap。

class UnnecessaryLock
{
    volatile bool m_locked;
    
public:
    void Acquire()
    {
        // assert no one already has the lock
        assert(!m_locked);
        
        // now lock (so we can detect overlapping
        // critical operations if they happen)
        m_locked = true;
    }

    void Release()
    {
        // assert correct usage (that Release()
        // is only called after Acquire())
        assert(m_locked);
        
        // unlock
        m_locked = false;
    }

};

#if ASSERTIONS_ENABLED
#define BEGIN_ASSERT_LOCK_NOT_NECESSARY(L) (L).Acquire()
#define END_ASSERT_LOCK_NOT_NECESSARY(L) (L).Release()
#else
#define BEGIN_ASSERT_LOCK_NOT_NECESSARY(L)
#define END_ASSERT_LOCK_NOT_NECESSARY(L)
#endif

// Example usage...
UnnecessaryLock g_lock;
void EveryCriticalOperation()
{
    BEGIN_ASSERT_LOCK_NOT_NECESSARY(g_lock);
    printf("perform critical op...\n");
    END_ASSERT_LOCK_NOT_NECESSARY(g_lock);
}

View Code

　　We could also wrap the locks in a janitor.

class UnnecessaryLockJanitor
{
    UnnecessaryLock* m_pLock;
public:
    explicit
    UnnecessaryLockJanitor(UnnecessaryLock& lock)
    : m_pLock(&lock) { m_pLock->Acquire(); }
    
    ~UnnecessaryLockJanitor() { m_pLock->Release(); }
};

#if ASSERTIONS_ENABLED
    #define ASSERT_LOCK_NOT_NECESSARY(J,L) \
    UnnecessaryLockJanitor J(L)
#else
    #define ASSERT_LOCK_NOT_NECESSARY(J,L)
#endif

// Example usage...
UnnecessaryLock g_lock;
void EveryCriticalOperation()
{
    ASSERT_LOCK_NOT_NECESSARY(janitor, g_lock);
    printf("perform critical op...\n");
}

View Code

　　We implemented this at Naughty Dog and it successfully caught a number of cases of critical operations overlapping when the programmers had assumed they never could do so.

16、Lock-Free Transactions

　　To perform a critical operation in a lock-free manner, we need to think of each such operation as a transaction that can either succeed in its entirety, or fail in its entirety. If it fails, the transaction is simply retried until it does succeed.

　　To implement any transaction, no matter how complex, we perform the majority of the work locally (i.e., using data that’s visible only to the current thread, rather than operating directly on the shared data). When all of our ducks are in a row and the transaction is ready to commit, we execute a single atomic instruction, such as CAS or LL/SC. If this atomic instruction succeeds, we have successfully “published” our transaction globally—it becomes a permanent part of the shared data structure on which we’re operating. But if the atomic instruction fails, that means some other thread was attempting to commit a transaction at the same time we were.

　　This fail-and-retry approach works because whenever one thread fails to commit its transaction, we know that it was because some other thread managed to succeed. As a result, one thread in the system is always making forward progress (just maybe not us). And that is the definition of lock-free.

17、A Lock-Free Linked List

template< class T >
class SList
{
    struct Node
    {
        T m_data;
        Node* m_pNext;
    };
    
    std::atomic< Node* > m_head { nullptr };
    
public:

    void push_front(T data)
    {
        // prep the transaction locally
        auto pNode = new Node();
        pNode->m_data = data;
        pNode->m_pNext = m_head;
        
        // commit the transaction atomically
        // (retrying until it succeeds)
        while (!m_head.compare_exchange_weak(
                pNode->m_pNext, pNode))
        { }
    }
};

View Code

　　注意，compare_exchange_weak 并不等于同 CAS。CAS为false时，并不会修改 expectedValue，但是 compare_exchange_weak会修改 expectedValue。所以上述代码 pNode->m_pNext 会自动更新。

18、SIMD/Vector Processing

　　SIMD and multithreading are combined into a form of parallelsm known single instruction multiple thread (SIMT), which forms the basis of all modern GPUs.

　　Intel first introduced its MMX instruction set with their Pentium line of CPUs in 1994. These instructions permitted SIMD calculations to be performed on eight 8-bit integers, four 16-bit integers, or two 32-bit integers packed into special 64-bit MMX registers.

　　MMX 为64位。

　　streaming SIMD extensions, or SSE, the first version of which appeared in the Pentium III processor. The SSE instruction set utilizes 128-bit registers that can contain integer or IEEE floating-point data.

　　SSE 为 128位。

　　The SSE mode most commonly used by game engines is called packed 32-bit floating-point mode. In this mode, four 32-bit float values are packed into a single 128-bit register. An operation such as addition or multiplication can thus be performed on four pairs of floats in parallel by taking two of these 128-bit registers as its inputs. Intel has since introduced various upgrades to the SSE instruction set, named SSE2, SSE3, SSSE3 and SSE4.

　　In 2011, Intel introduced a new, wider SIMD register file and accompanying instruction set named advanced vector extensions (AVX). AVX registers are 256 bits wide, permitting a single instruction to operate on pairs of up to eight 32-bit floating-point operands in parallel. The AVX2 instruction set is an extension to AVX. Some Intel CPUs now support AVX-512, an extension to AVX permitting 16 32-bit floats to be packed into a 512-bit register.

　　Avx 为256位， Avx-512为 512位。

19、The SSE Instruction Set and Its Registers

　　These instructions are denoted with a ps suffix, indicating that we’re dealing with packed data (p), The SSE registers are named XMMi, where i is an integer between 0 and 15. In packed 32-bit floating-point mode, each 128-bit XMMi register contains four 32-bit floats.

　　In AVX, the registers are 256 bits wide and are named YMMi; in AVX-512, they are 512 bits in width and are named ZMMi.　　

20、The __m128 Data Type

　　Declaring automatic variables and function arguments to be of type __m128 often results in the compiler treating those values as direct proxies for SSE registers.

　　自动变量、函数参数的 __m126 会编译成对 SSE register 的使用。

　　But using the __m128 type to declare global variables, structure/class members, and sometimes local variables results in the data being stored as a 16-byte aligned array of float in memory.

　　全局变量、成员变量会编译成128 bit 对齐的内存数据。

　　Using a memory-based __m128 variable in an SSE calculation will cause the compiler to implicitly emit instructions for loading the data from memory into an SSE register prior to performing the calculation on it, and likewise to emit instructions for storing the results of the calculation back into the memory that “backs” each such variable.

21、Alignment of SSE Data

　　Whenever data that is intended for use in an XMMi register is stored in memory, it must be 16-byte (128-bit) aligned. Likewise.

　　The compiler ensures that global and local variables of type __m128 are aligned automatically. It also pads struct and class members so that any __m128 members are aligned properly relative to the start of the object, and ensures that the alignment of the entire struct or class is equal to the worstcase alignment of its members.

22、SSE Compiler Intrinsics

　　modern compilers provide intrinsics—special syntax that looks and behaves like a regular C function, but is actually boiled down to inline assembly code by the compiler.

　　In order to use SSE and AVX intrinsics, your .cpp file must #include <xmmintrin.h> in Visual Studio, or <x86intrin.h> when compiling with Clang or gcc.

23、Some Useful SSE Intrinsics

　　• __m128 _mm_set_ps(float w, float z, float y, float x);

　　• __m128 _mm_load_ps(const float* pData);

　　• void _mm_store_ps(float* pData, __m128 v);

　　• __m128 _mm_add_ps(__m128 a, __m128 b);

　　• __m128 _mm_mul_ps(__m128 a, __m128 b);

#include <xmmintrin.h>

void TestAddSSE()
{
    alignas(16) float A[4];
    alignas(16) float B[4] = { 2.0f, 4.0f, 6.0f, 8.0f };
    
    // set a = (1, 2, 3, 4) from literal values, and
    // load b = (2, 4, 6, 8) from a floating-point array
    // just to illustrate the two ways of doing this
    // (remember that _mm_set_ps() is backwards!)
    __m128 a = _mm_set_ps(4.0f, 3.0f, 2.0f, 1.0f);
    __m128 b = _mm_load_ps(&B[0]);
    
    // add the vectors
    __m128 r = _mm_add_ps(a, b);
    
    // store '__m128 a' into a float array for printing
    _mm_store_ps(&A[0], a);
    
    // store result into a float array for printing
    alignas(16) float R[4];
    _mm_store_ps(&R[0], r);
    
    // inspect results
    printf("a = %.1f %.1f %.1f %.1f\n", A[0], A[1], A[2], A[3]);
    printf("b = %.1f %.1f %.1f %.1f\n", B[0], B[1], B[2], B[3]);
    printf("r = %.1f %.1f %.1f %.1f\n", R[0], R[1], R[2], R[3]);
}

View Code

24、Using SSE to Vectorize a Loop

void AddArrays_ref(int count, 
                    float* results,
                    const float* dataA,
                    const float* dataB)
{
    for (int i = 0; i < count; ++i)
    {
        results[i] = dataA[i] + dataB[i];
    }
}

View Code

　　上面的代码，使用SSE优化后如下。

void AddArrays_sse(int count,
                    float* results,
                    const float* dataA,
                    const float* dataB)
{
    // NOTE: the caller needs to ensure that the size of
    // all 3 arrays are equal, and a multiple of four!
    assert(count % 4 == 0);
    for (int i = 0; i < count; i += 4)
    {
        __m128 a = _mm_load_ps(&dataA[i]);
        __m128 b = _mm_load_ps(&dataB[i]);
        __m128 r = _mm_add_ps(a, b);
        _mm_store_ps(&results[i], r);
    }
}

View Code

　　This is called vectorizing our loop.

　　This particular example isn’t quite four times faster, due to the overhead of having to load the values in groups of four and store the results on each iteration; but when I measured these functions running on very large arrays of floats, the nonvectorized loop took roughly 3.8 times as long to do its work as the vectorized loop.

25、Vectorized Dot Products

void DotArrays_ref(int count,
                    float r[],
                    const float a[],
                    const float b[])
{
    for (int i = 0; i < count; ++i)
    {
        // treat each block of four floats as a
        // single four-element vector
        const int j = i * 4;
        r[i] = a[j+0]*b[j+0] // ax*bx
             + a[j+1]*b[j+1] // ay*by
             + a[j+2]*b[j+2] // az*bz
             + a[j+3]*b[j+3]; // aw*bw
    }
}

View Code

_mm_hadd_ps() (horizontal add). This intrinsic operates on a single input register (x, y, z,w) and calculates two sums: s = x +y and t = z+w. It stores these two sums into the four slots of the destination register as (t, s, t, s). Performing this operation twice allows us to calculate the sum d = x +y+z+w. This is called adding across a register.

　　first attempt at using SSE intrinsics:

void DotArrays_sse_horizontal(int count,
                                float r[],
                                const float a[],
                                const float b[])
{
    for (int i = 0; i < count; ++i)
    {
        // treat each block of four floats as a
        // single four-element vector
        const int j = i * 4;
        __m128 va = _mm_load_ps(&a[j]); // ax,ay,az,aw
        __m128 vb = _mm_load_ps(&b[j]); // bx,by,bz,bw
        __m128 v0 = _mm_mul_ps(va, vb);
        
        // add across the register...
        __m128 v1 = _mm_hadd_ps(v0, v0);
        
        // (v0w+v0z, v0y+v0x, v0w+v0z, v0y+v0x)
        __m128 vr = _mm_hadd_ps(v1, v1);
        
        // (v0w+v0z+v0y+v0x, v0w+v0z+v0y+v0x,
        // v0w+v0z+v0y+v0x, v0w+v0z+v0y+v0x)
        _mm_store_ss(&r[i], vr); // extract vr.x as a float
    }
}

View Code

　　上面的第一个优化代码. Adding across a register is not usually a good idea because it’s a very slow operation. Profiling the DotArrays_sse() implementation shows that it actually takes a little bit more time than the reference implementation. Using SSE here has actually slowed us down!12

　　A better approach. 优化掉耗时的 _mm_hadd_ps().注意输入是：By storing them in transposed order。

void DotArrays_sse(int count,
                    float r[],
                    const float a[],
                    const float b[])
{
    for (int i = 0; i < count; i += 4)
    {
        __m128 vaX = _mm_load_ps(&a[(i+0)*4]); // a[0,4,8,12]
        __m128 vaY = _mm_load_ps(&a[(i+1)*4]); // a[1,5,9,13]
        __m128 vaZ = _mm_load_ps(&a[(i+2)*4]); // a[2,6,10,14]
        __m128 vaW = _mm_load_ps(&a[(i+3)*4]); // a[3,7,11,15]
        __m128 vbX = _mm_load_ps(&b[(i+0)*4]); // b[0,4,8,12]
        __m128 vbY = _mm_load_ps(&b[(i+1)*4]); // b[1,5,9,13]
        __m128 vbZ = _mm_load_ps(&b[(i+2)*4]); // b[2,6,10,14]
        __m128 vbW = _mm_load_ps(&b[(i+3)*4]); // b[3,7,11,15]
        
        __m128 result;
        result = _mm_mul_ps(vaX, vbX);
        result = _mm_add_ps(result, _mm_mul_ps(vaY, vbY));
        result = _mm_add_ps(result, _mm_mul_ps(vaZ, vbZ));
        result = _mm_add_ps(result, _mm_mul_ps(vaW, vbW));
        
        _mm_store_ps(&r[i], result);
    }
}

View Code

26、The MADD Instruction

　　It’s interesting to note that a multiply followed by an add is such a common operation that it has its own name—madd.

　　前面代码中的 _mm_add_ps(result, _mm_mul_ps(vaY, vbY)); 可以用另一个函数来替代 madd。

27、Transpose as We Go

　　25中的最后一个示例，要求输入的 a、b 是 transpose的。但通常我们面对的是正常存储的数据，为了transpose，可以使用 TRANSPOSE4() 方法。

void DotArrays_sse_transpose(int count,
                                float r[],
                                const float a[],
                                const float b[])
{
    for (int i = 0; i < count; i += 4)
    {
        __m128 vaX = _mm_load_ps(&a[(i+0)*4]); // a[0,1,2,3]
        __m128 vaY = _mm_load_ps(&a[(i+1)*4]); // a[4,5,6,7]
        __m128 vaZ = _mm_load_ps(&a[(i+2)*4]); // a[8,9,10,11]
        __m128 vaW = _mm_load_ps(&a[(i+3)*4]); // a[12,13,14,15]
        __m128 vbX = _mm_load_ps(&b[(i+0)*4]); // b[0,1,2,3]
        __m128 vbY = _mm_load_ps(&b[(i+1)*4]); // b[4,5,6,7]
        __m128 vbZ = _mm_load_ps(&b[(i+2)*4]); // b[8,9,10,11]
        __m128 vbW = _mm_load_ps(&b[(i+3)*4]); // b[12,13,14,15]
        
        _MM_TRANSPOSE4_PS(vaX, vaY, vaZ, vaW);
        // vaX = a[0,4,8,12]
        // vaY = a[1,5,9,13]
        // ...
        
        _MM_TRANSPOSE4_PS(vbX, vbY, vbZ, vbW);
        // vbX = b[0,4,8,12]
        // vbY = b[1,5,9,13]
        // ...
        
        __m128 result;
        result = _mm_mul_ps(vaX, vbX);
        result = _mm_add_ps(result, _mm_mul_ps(vaY, vbY));
        result = _mm_add_ps(result, _mm_mul_ps(vaZ, vbZ));
        result = _mm_add_ps(result, _mm_mul_ps(vaW, vbW));
        _mm_store_ps(&r[i], result);
    }
}

View Code

　　Profiling all three implementations of DotArrays() shows that our final version (the one that transposes the vectors as it goes) is roughly 3.5 times faster than the reference implementation.

28、Shuffle and Transpose

　　 here’s what the _MM_TRANSPOSE() macro looks like:

#define _MM_TRANSPOSE4_PS(row0, row1, row2, row3) \
{ __m128 tmp3, tmp2, tmp1, tmp0; \
    \
    tmp0 = _mm_shuffle_ps((row0), (row1), 0x44); \
    tmp2 = _mm_shuffle_ps((row0), (row1), 0xEE); \
    tmp1 = _mm_shuffle_ps((row2), (row3), 0x44); \
    tmp3 = _mm_shuffle_ps((row2), (row3), 0xEE); \
    \
    (row0) = _mm_shuffle_ps(tmp0, tmp1, 0x88); \
    (row1) = _mm_shuffle_ps(tmp0, tmp1, 0xDD); \
    (row2) = _mm_shuffle_ps(tmp2, tmp3, 0x88); \
    (row3) = _mm_shuffle_ps(tmp2, tmp3, 0xDD); }

View Code

　　Mask 的来源为：

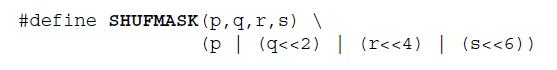
　　_mm_shuffle_ps() 的完整涵义为：

29、Vector-Matrix Multiplication with SSE

　　Vector-Matrix 本质上与 VectorDot 的计算过程是一样的。所以实现原理类似。

union Mat44
{
    float c[4][4]; // components
    __m128 row[4]; // rows
};

__m128 MulVecMat_sse(const __m128& v, const Mat44& M)
{
    // first transpose v
    __m128 vX = _mm_shuffle_ps(v, v, 0x00); // (vx,vx,vx,vx)
    __m128 vY = _mm_shuffle_ps(v, v, 0x55); // (vy,vy,vy,vy)
    __m128 vZ = _mm_shuffle_ps(v, v, 0xAA); // (vz,vz,vz,vz)
    __m128 vW = _mm_shuffle_ps(v, v, 0xFF); // (vw,vw,vw,vw)

    __m128 r = _mm_mul_ps(vX, M.row[0]);
    
    r = _mm_add_ps(r, _mm_mul_ps(vY, M.row[1]));
    r = _mm_add_ps(r, _mm_mul_ps(vZ, M.row[2]));
    r = _mm_add_ps(r, _mm_mul_ps(vW, M.row[3]));\
    
    return r;
}

View Code

30、Matrix-Matrix Multiplication with SSE

　　矩阵-矩阵相乘，分别计算前一矩阵的每一行，让前一矩阵的每一行分别与后面的矩阵进行 Vector-Matrix Multiplication运算。

void MulMatMat_sse(Mat44& R, const Mat44& A, const Mat44& B)
{
    R.row[0] = MulVecMat_sse(A.row[0], B);
    R.row[1] = MulVecMat_sse(A.row[1], B);
    R.row[2] = MulVecMat_sse(A.row[2], B);
    R.row[3] = MulVecMat_sse(A.row[3], B);
}

View Code

31、Generalized Vectorizaton

　　Interestingly, most optimizing compilers can vectorize some kinds of singlelane loops automatically. In fact, when writing the above examples, it took some doing to force the compiler not to vectorize my single-lane code, so that I could compare its performance to my SIMD implementation!

32、Vector Predication

　　下面是一个普通函数，用于计算平方根。

#include <cmath>

void SqrtArray_ref(float* __restrict__ r,
const float* __restrict__ a,

int count)
{
    for (unsigned i = 0; i < count; ++i)
    {
        if (a[i] >= 0.0f)
            r[i] = std::sqrt(a[i]);
        else
            r[i] = 0.0f;
    }
}

View Code

　　下面是第一个SSE优化，但是在除0的部分有问题。

#include <xmmintrin.h>

void SqrtArray_sse_broken(float* __restrict__ r,
const float* __restrict__ a,

int count)
{
    assert(count % 4 == 0);
    __m128 vz = _mm_set1_ps(0.0f); // all zeros
    for (int i = 0; i < count; i += 4)
    {
        __m128 va = _mm_load_ps(a + i);
        __m128 vr;
        if (_mm_cmpge_ps(va, vz)) // ???
            vr = _mm_sqrt_ps(va);
        else
            vr = vz;
        _mm_store_ps(r + i, vr);
    }
}

View Code

　　_mm_cmpge_ps() produce a four component result, stored in an SSE register. the result consists of four 32-bit masks. Each mask contains all binary 1s (0xFFFFFFFFU) if the corresponding component in the input register passed the test, and all binary 0s (0x0U) if that component failed the test.

　　将 _mm_cmpge_ps 的返回值与 sqrt 的结果相 & 就得到正确的结果。注意，下面取结果的代码略显麻烦。

#include <xmmintrin.h>

void SqrtArray_sse(float* __restrict__ r,
const float* __restrict__ a,

int count)
{
    assert(count % 4 == 0);
    __m128 vz = _mm_set1_ps(0.0f);
    for (int i = 0; i < count; i += 4)
    {
        __m128 va = _mm_load_ps(a + i);
        
        // always do the quotient, but it may end
        // up producing QNaN in some or all lanes
        __m128 vq = _mm_sqrt_ps(va);
        
        // now select between vq and vz, depending
        // on whether the input was greater than
        // or equal to zero or not
        __m128 mask = _mm_cmpge_ps(va, zero);
        
        // (vq & mask) | (vz & ~mask)
        __m128 qmask = _mm_and_ps(mask, vq);
        __m128 znotmask = _mm_andnot_ps(mask, vz);
        __m128 vr = _mm_or_ps(qmask, znotmask);
        _mm_store_ps(r + i, vr);
    }
}

View Code

　　SSE4—it is emitted by the intrinsic _mm_blendv_ps(). Let’s take a look at how we might implement a vector select operation ourselves. We can write it like this:

__m128 _mm_select_ps(const __m128 a,
                    const __m128 b,
                    const __m128 mask)
{
    // (b & mask) | (a & ~mask)
    __m128 bmask = _mm_and_ps(mask, b);
    __m128 anotmask = _mm_andnot_ps(mask, a);
    return _mm_or_ps(bmask, anotmask);
}

View Code

　　也可以使用异或来实现 select函数。

__m128 _mm_select_ps(const __m128 a,
                        const __m128 b,
                        const __m128 mask)
{
    // (((a ^ b) & mask) ^ a)
    __m128 diff = _mm_xor_ps(a, b);
    return _mm_xor_ps(a, _mm_and_ps(mask, diff));
}

View Code

33、

34、

35、

posted on 2019-03-14 15:48 Tekkaman 阅读(480) 评论(0) 编辑收藏举报

刷新页面返回顶部

导航