【3D Math Keynote 3】
1、球的表面积 Surface、球的体积 Volumn：
2、当物体旋转后，如果通过变换后的旧AABB来顶点来计算新的AABB顶点，则生成的新AABB可能比实际的新AABB大一些。
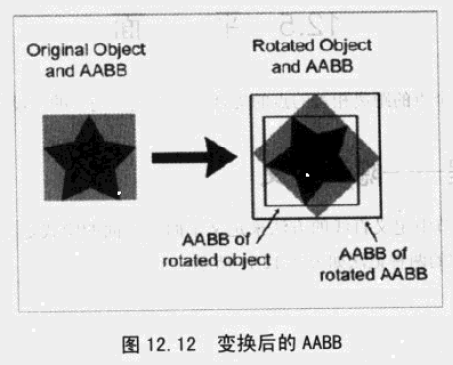
由 旧AABB 快速计算 新AABB的方法。
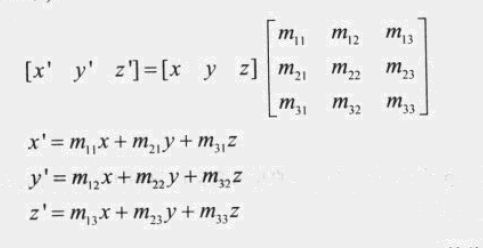
如果 m < 0，则取min值参与计算，如果 m > 0，则取max值参与计算。
3、多于3个点的最佳平面。算法就是求出所有的n，然后求个平均值。（此公式书中未给出证明过程）
使用求和符号，能使公式更简洁一些。
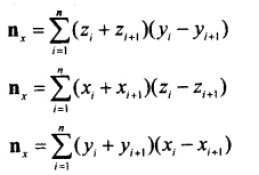
最佳d值为：
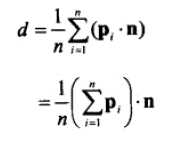
4、点到平面的距离。比如平面外有一点q，求q到平面的距离。
5、三角形的正弦、余弦公式。
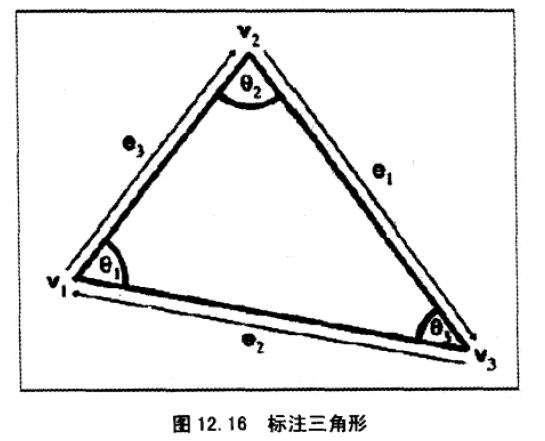
海伦公式，让我们可以使用三边长度，计算出面积：
6、根据三个顶点坐标，快速计算三角形面积。
顺时针，依次每条边与x轴围成的面积。
A(e1) + A(e2) + A(e3) 即是三角形面积。
可以看到如果将三角形下移h高度，使得三角形与X轴穿叉，面积实际上不会变。
A(e1) = (y3+y2-h)(x3-x2)/2，将-h提取出来，得到 -hx3+hx2
A(e2) = (y1+y3-h)(x1-x3)/2，将-h提取出来，得到 -hx1+hx3
A(e3) = (y2+y1-h)(x2-x1)/2，将-h提取出来，得到 -hx2+hx1
可以看到，上面三个A中新增出来的项，刚好相互抵消。所以即使三角形与X轴相互穿叉，上述算法也能得到正确的面积。
最后，最简单的方法实际是计算叉积，叉积即是面积。
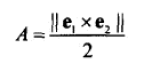
7、三角形局部坐标，通常可以使用重心坐标。
每个顶点对应的边上的每一个点的对应分量为0。
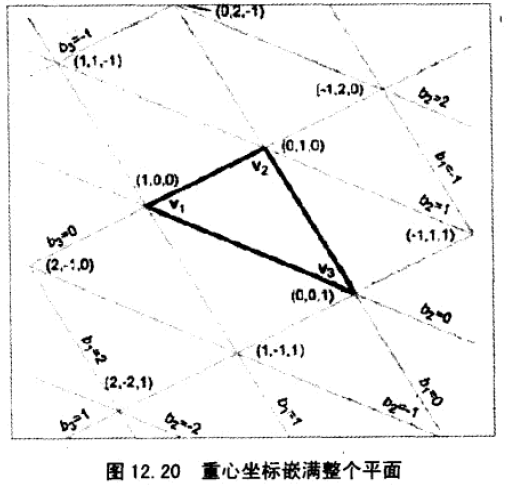
重心坐标不同于笛卡尔坐标，笛卡尔有2个维度的变量，重点坐标却有3个维度的变化。由于 b1+b2+b3=1，所以实际上，在重心坐标系下，只要两个维度就能惟一确定一个位置。
8、给定 v1,v2,v3和p，计算 p 的重心坐标。
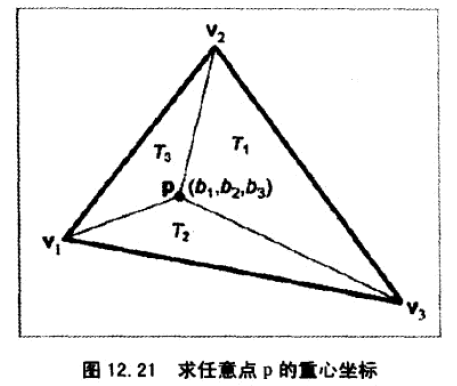
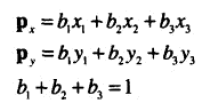
重心坐标实际是面积比。
9、计算3D中任意点的重心坐标。
一种算法是通过抛弃 x,y,z 中的一个分量，将3D问题转化到 2D 中。
但存在一个问题，如果投影后三点或两点共线怎么办。一种解决方法是，挑选投影面积最大的那一面来计算。实际计算方法就是，抛弃法向量中分量最大的那一个轴。
另一种算法是使用公式 12.23 中的面积比法，计算p点与各边围成的面积，求出比例。
10、重心或质心。
内心是指到三角形各边相等的点。之所以称之为内心，是因为它是三角形内切圆的圆心。内心是角平分线的交点。
外心是到三角形各顶点距离相等的点，是三角形外接圆的圆心。
11、简单多边形不包含洞，复杂多边形可能包含洞。
凸多边形任意两点连续均在图形内，凹多边形有可能在图形外。怎样才能知道一个多边形是凹的还是凸的?一种方法是检查n个顶点的较小角的和（解决凹多边形的问题）， 是否为 (n-2)*180。
凸多边形的补角和为 360 度。
另一个检测凹凸多边形的方法是每一个点的转身，用叉乘来做。
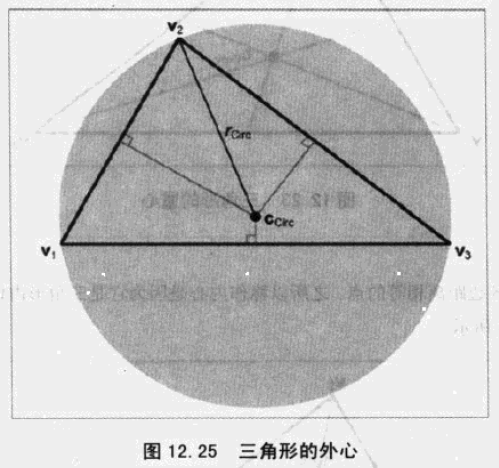
12、点距直线的最接近点。
13、点距射线的最接近点。
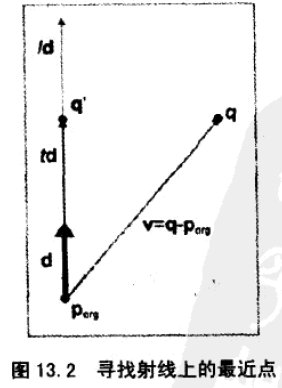
14、点到平面的最接近点。与12中的点到直接的最接近点公式一样，只是多了一维。
15、点到圆或球的最接近点。
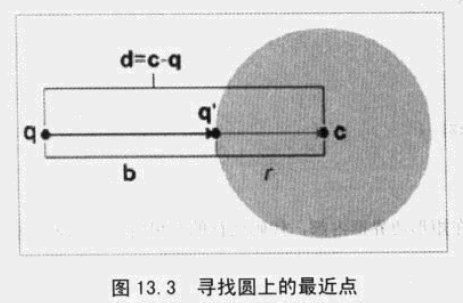
16、计算AABB上的最接近点。
算法是按一定顺序，沿着每条轴将 q 推 B。
17、2D 中隐式直接相交性检测。
18、3D中两条射线的相交检测。
19、射线和平面的相交性检测。
上述公式是通过代数的方程的方法来解。
根据公式，可以提供另一种理解方法。 d-p0*n 其实是 p0到平面的距离，d*n其实是d与n平行的分向量。总距离除以向量步行，即可得到t的值。
20、AABB和平面的相交性检测。
动态检测：
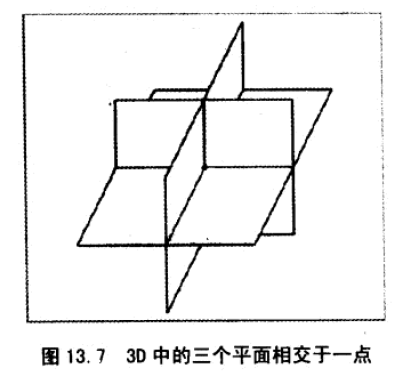
21、三平面相交性检测。算法与2D中两直线相交性检测类似，解方程。
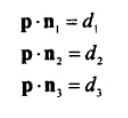
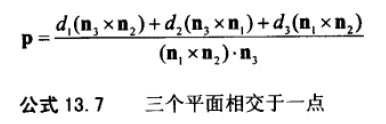
22、射线和圆、球的相交性检测。
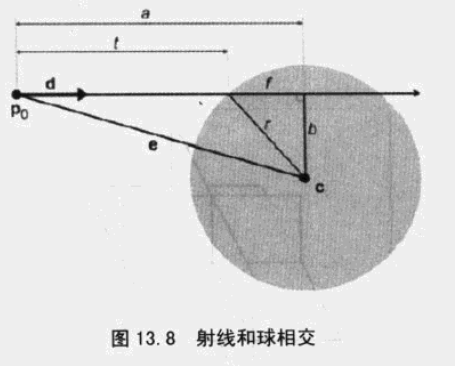
上图中 a可以通过 e到射线的投影计算出来。
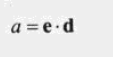
b 可以通过 e、a求出来。
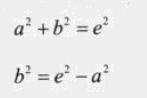
f 可以通过 r、b求出来。
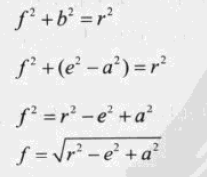
t 可以通过 a、f求出来。
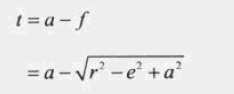
23、两个圆球的相交性检测。
两个运动的球需要通过相对运动来计算。
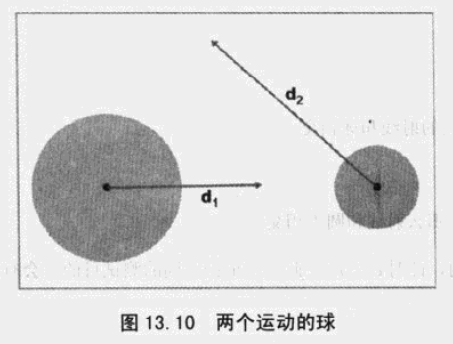
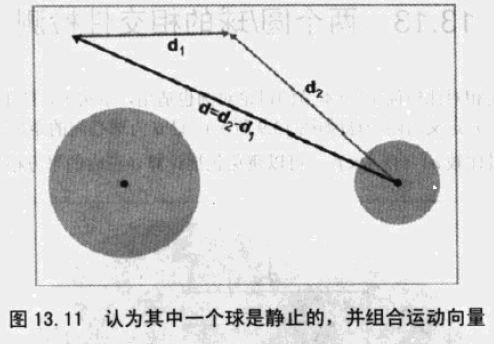
通过相对运动，将问题转化成了如下模型：
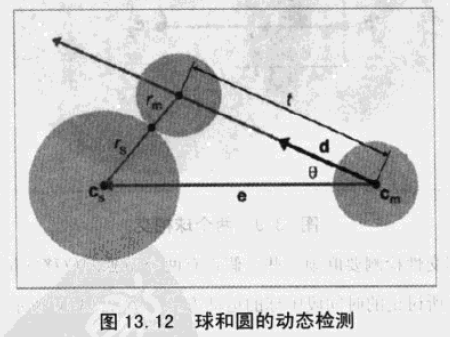
根据 cos 定理，有如下公式：
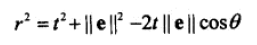
24、球和AABB的相交性检测。
选择 min/ max，取一个最小 magnitude， 看是否小于距离。
25、球和平面的相交性检测。
计算圆心到平面的距离，看是否小于r。
如果圆在运行中，如何求解t为何值时与平面碰撞？
问题转化成了点到平面的距离。
26、射线和三角形的相交性检测。
第一步，计算射线到三角形平面的交点。第二步，通过计算交点的重心主坐标，来判断它是否在三角形中。
27、射线和AABB的相交性检测。
书中未详细说明算法。
28、两个AABB的相交性检测。
检测两个AABB是否相交非常简单，只要在每一维上检查它们的重合度即可。如果所有维上都没有重合，那么这两个AABB就不会相交。
动态情况麻烦一点，如果向某方向以d运行，求t时刻相遇。t为所有维上同时重合的第一个点。
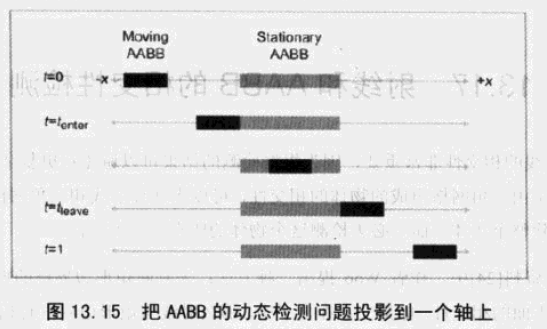
所有时间区间的交集，就是两个边界框相交的时间段。
29、
30、
31、
32、
33、
