【3D Math Keynote 2】
1、方向（diretion），指的是前方朝向。方位（orientation），指的是head、pitch、roll。
2、欧拉角的缺点：
1）给定方位的表达式不惟一。
例如，pitch 135 = heading180 + pitch 45 + bank 180。
通过将 heading、bank 限制在 +180~-180度，pitch限制在+90~-90度即可解决不惟一的问题。
2）两个角度间插值非常困难。
3、复数的共轭
复数的模。
4、复数集存在于一个2D平面上，可以认为这个平面有2个轴：实轴、虚轴。
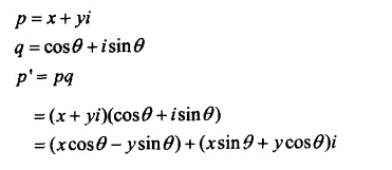
四元数有3个虚部，i、j、k。
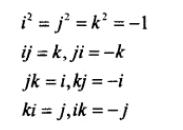
绕向量 n 旋转 0 度的四元数：
q与-q代表的实际角位移是相同的，将0 加上360度，不会改变q的角位移，但q的四个分量都变负了。所以任意角位移有2种四元数的表示法。
四元数也有模。
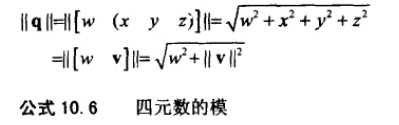
5、四元数的共轭：
四元数的逆：
当 |q| 为1时，四元数的共轭，就是四元数的逆。
单位四元数：[1, 0]
四元数逆意味着向相反的方向旋转相同的角度。
6、四元数乘法。
四元数乘法满足结合律，不满足交换律。
四元数叉乘的模等于模的积：
四元数逆的性质：
7、四元数旋转公式：
下例，先执行a旋转，再执行b旋转：
8、四元数点乘。结果是一个标量。
9、四元数的对数。引入变量 alpha = 0/2
指数公式为：
9.1、四元数求幂。我们看看它的数学定义。
结合9中的公式，上式可以推导为 exp(t[0 alpha*n])，也就是 q^t次方，其实是 alpha 乘以了t。所以q^t实际上是 [cos(t*alpha) n.sin(t*alpha)]。
下述代码使用上述原理，计算四元数 q 的 t 次方的值。原理是让角度 alpha * t。
上面的 if 是用于避免单位四元数[1 0]的情况，单位四元数放大 t 倍，还是单位四元数。
10、slerp 避免了欧拉角插值的所有问题。四元数插值的理论：
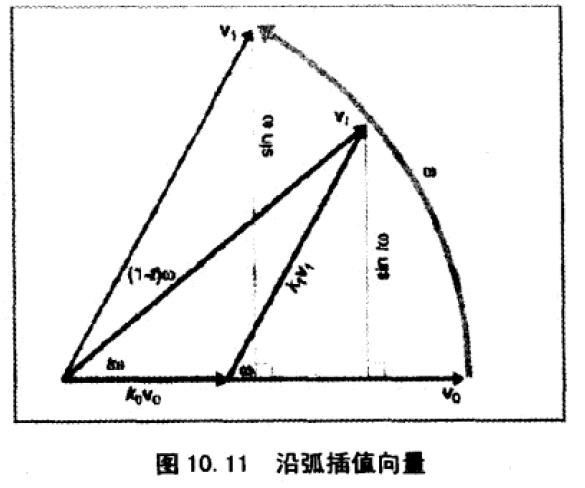
旋转插值图解：
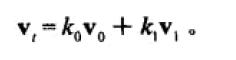
由相似三角形原理，可以求出 k0、k1。
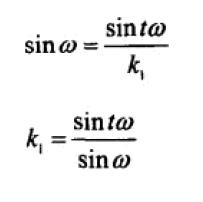
所以 V(t) 可以表示为：
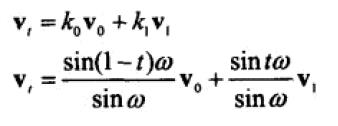
扩展到四元数即为：
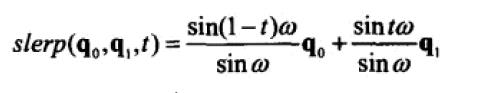
slerp 的完整代码如下：
上述实现用了一个书上未证明的公式，四元数的点乘等于夹角的 cos。
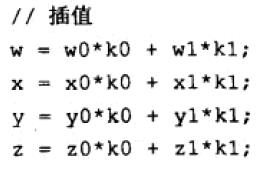
11、squard 是四元数的样条插值。需要引入控制点：
可以看到，Si的计算需要引用 qi-1、qi、qi+1。所以在计算转变时，实际需要四个 q点。
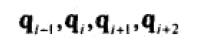
样条插值轨迹为：
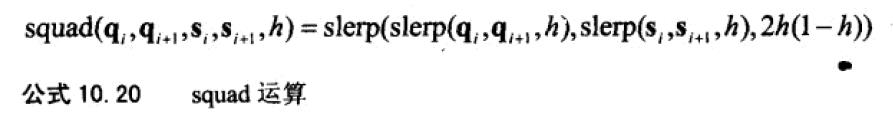
12、从欧拉角到矩阵。
从惯性坐标系到物体坐标系非常容易，将3个轴轴的旋转矩阵相乘即可。
而从物体坐标系到惯性坐标系，取上面矩阵的转置矩阵即可。
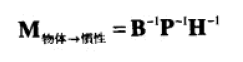
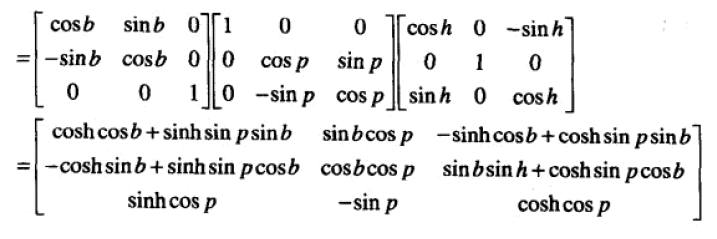
13、从矩阵到欧拉角
上面求解出了 pitch，也就推出了 cosp 的值。从而根据 m13、m33 可以推出 sinh、cosh 的的值，然后使用 atan2 即可计算出 h。
用同样的方式，可以用m21、m22解得 bank。
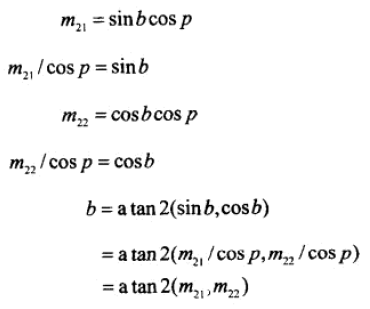
若 cosp 为0，则可推出 p 是+/- 90，b 为0。从而可以使用下面的值化简公式：
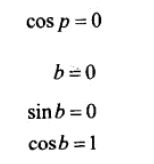
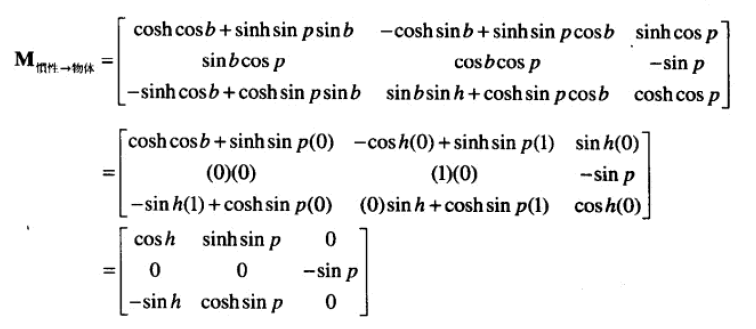
通过 m11、m31 可计算出h。
14、实现从矩阵解出欧拉角的算法。
// 设矩阵保存在下面这些变量中 float m11, m12, m13; float m21,m22,m23; float m31,m32,m33; // 以弧度形式计算欧拉角并存在以下变量中 float h,p,b; // 从m23计算pitch, 小心 asin() 的域错误，因浮点计算我们允许一定的误差 float sp = -m23; if (sp <= -1.0f){ p = -1.570796f; // -pi/2 }else if (sp >= 1.0){ p = 1.570796; // pi/2 } else { p = asign(sp); } // 检查万象锁的情况，允许一些误差 if (sp > 0.9999f){ // 向正上或正下看 // 将 bank 置零，赋值给 heading b = 0.0f; h = atan2(-m32, m11); } else { // 通过 m12 和 m33 计算heading h = atan2(m12, m33); b = atan2(m21, m22); }
15、从四元数转换到矩阵。
绕任意轴的旋转矩阵：
绕任意轴旋转的四元数：
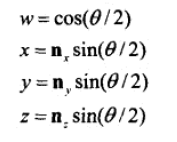
我们需要把每一个m推导成为 w,x,y,z 的形式，以m11为例。
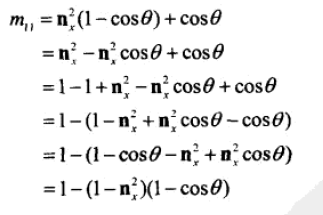
使用 cos 倍角公式：
最后展开化简可得：
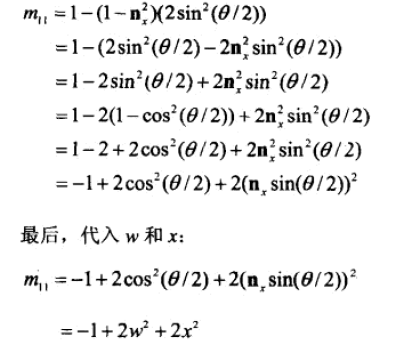
其他m求法的就不举例了，是类似的方法。下面是最终答案，从四元数构造出的完整旋转矩阵：
16、从矩阵转换到四元数。
从直接利用公式 10.23，首先检查对角线元素。
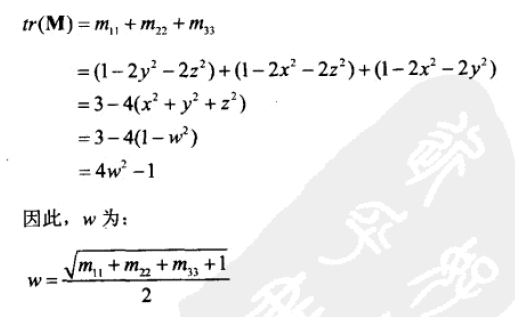
可以用有类似的方法求得其他三个元素：
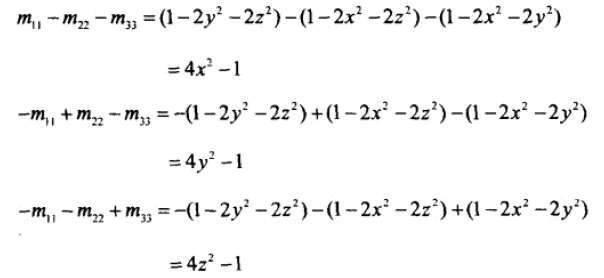
因为平方根的结果总是正。另一个技术是检查对称位置上的元素和。
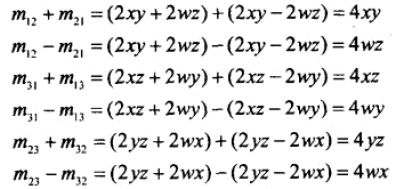
首先用第一种方法计算出 w,x,y,z 其中一个的值，然后再用第二种方法，得出另外三个数值的值，即可避免所有元素均为正的问题。
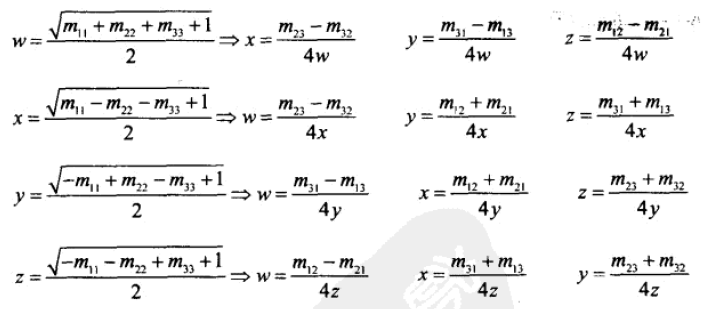
下面是算法实现：
// 输入矩阵 float m11, m12, m13; float m21, m22, m23; float m31, m32, m33; // 输出四元数 float w, x, y, z; // 探测 w, x, y, z 中的最大绝对值 float fourWSquaredMinus1 = m11 + m22 +m33; float fourXSquaredMinus1 = m11 - m22 - m33; float fourYSquaredMinus1 = m22-m11-m33; float fourZSquaredMinus1 = m33 - m11 -m33; int biggestIndex = 0; float fourBiggestSquaredMinus1 = fourWSquaredMinus1; if (fourXSquaredMinus1 > fourBiggestSquaredMinus1){ fourBiggestSquaredMinus1 = fourXSquaredMinus1; biggestIndex = 1; } if (fourYSquaredMinus1 > fourBiggestSquaredMinus1){ fourBiggestSquaredMinus1 = fourYSquaredMinus1; biggestIndex = 2; } if (fourZSquaredMinus1 > fourBiggestSquaredMinus1){ fourBiggestSquaredMinus1 = fourZSquaredMinus1; biggestIndex = 3; } // 计算平方根和除法 float biggestVal = sqrt(fourBiggestSquaredMinus1 + 1.0f) * 0.5f; float mult = 0.25f / biggestVal; // 计算四元数的值 switch(biggestIndex){ case 0: w = biggestVal; x = (m23-m32)*mult; y = (m31-m13)*mult; z = (m12 - m21) * mult; break; case 1: x = biggestVal; w = (m23-m32)*mult; y = (m12+m21)*mult; z = (m31+m12)*mult; break; case 2: y = biggestVal; w = (m31 - m13) * mult; x = (m12 + m21) * mult; z = (m23 + m32) * mult; break; case 3: z = biggestVal; w = (m12 - m21) * mult; x = (m31 + m13) * mult; y = (m23 + m32) * mult; break; }
17、从欧拉角转换到四元数。
先将三个轴的旋转分别转换为四元数，再将这三个四元数连接成一个四元数。下面是分别旋转的四元数：
将其连接起来即可得到结果。
18、从四元转换到欧拉角
我们已经知道从四元数到矩阵，也知道从矩阵到欧拉角。下面是从矩阵求欧拉角：
再下面是四元数求矩阵：
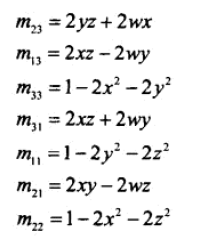
将图一中的 m 全部替换为 wxyz，即可得四元数到欧拉角的推导公式。
// 使用全局变量保存输入输出 float w,x,y,z; float h,p,b; // 计算 si(pitch) float sp = -2.0f * (y*z + w*x); // 检查万向锁，允许有一定误差 if (fabs(sp)>0.9999f){ // 向正上或正下看 p = 1.570796f * sp; // 计算 heading, bank 置零 h = atan2(-x*z - w*y, 0.5f - y*y - z*z); b = 0.0f; }else{ // 计算角度 p = asin(sp); h = atan2(x*z - w*y, 0.5f - x*x - y*y); b = atan2(x*y - w*z, 0.5f - x*x, -z*z); }
19、
20、
