圈复杂度计算实例
个人学习笔记, 网上摘抄.
计算公式1：V(G)=e-n+2p。其中，
e表示控制流图中边的数量，
n表示控制流图中节点的数量，
p图的连接组件数目（图的组件数是相连节点的最大集合）。因为控制流图都是连通的，所以p为1.
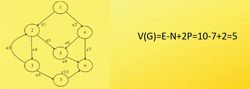
计算公式2：
V(G)=区域数=判定节点数+1。
其实，圈复杂度的计算还有更直观的方法，
因为圈复杂度所反映的是“判定条件”的数量，
所以圈复杂度实际上就是等于判定节点的数量再加上1，也即控制流图的区域数。
对于多分支的CASE结构或IF-ELSEIF-ELSE结构，
统计判定节点的个数时需要特别注意一点，要求必须统计全部实际的判定节点数，也即每个ELSEIF语句，
以及每个CASE语句，都应该算为一个判定节点。
计算公式3：V(G)=R。其中R代表平面被控制流图划分成的区域数。
针对程序的控制流图计算圈复杂度V(G)时，最好还是采用第一个公式，也即V(G)=e-n+2；
而针对模块的控制流图时，可以直接统计判定节点数，
这样更为简单；针对复杂的控制流图是，使用区域计算公式V(G)=R更为简单。
圈复杂度(Cyclomatic Complexity)是一种代码复杂度的衡量标准。
它可以用来衡量一个模块判定结构的复杂程度，数量上表现为独立现行路径条数，
也可理解为覆盖所有的可能情况最少使用的测试用例数。
圈复杂度大说明程序代码的判断逻辑复杂，可能质量低且难于测试和维护。
程序的可能错误和高的圈复杂度有着很大关系。
各判断语句的控制流图
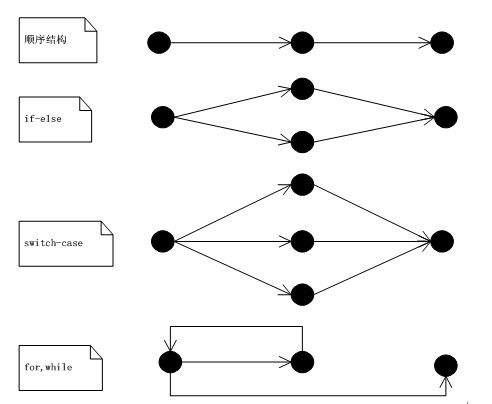
在计算圈复杂度时，可以通过程序控制流图方便的计算出来。
通常使用的计算公式是V(G) = e – n + 2 ,
e 代表在控制流图中的边的数量（对应代码中顺序结构的部分），
n 代表在控制流图中的节点数量，包括起点和终点（1、所有终点只计算一次，即便有多个return或者throw；2、节点对应代码中的分支语句）。
//程序原代码，圈复杂度为 2
public String case1(int num) {
String string = null;
if (num == 1) {
string = "String";
}
return string.substring(0);
}
//上面代码的单元测试代码
public void testCase1(){
String test1 = case1(1);
}
知道了如何计算圈复杂度，我们来使用控制流图重新计算一次case1方法的圈复杂度，其控制流图如下图。状态1表示if（num == 1 ）的条件判断，状态2表示string=”String”的赋值操作。可以通过下面的控制流图得到 e = 3 ; n = 3;那么全复杂度V(G) = 3 - 3 + 2 = 2,既case1的圈复杂度为2。
圈复杂度主要与分支语句（if、else、，switch 等）的个数成正相关。
可以在图1中看到常用到的几种语句的控制流图（表示程序执行流程的有向图）。
当一段代码中含有较多的分支语句，其逻辑复杂程度就会增加。
===========================================================================
public String case2(int index, String string) {
String returnString = null;
if (index < 0) {
throw new IndexOutOfBoundsException("exception <0 ");
}
if (index == 1) {
if (string.length() < 2) {
return string;
}
returnString = "returnString1";
} else if (index == 2) {
if (string.length() < 5) {
return string;
}
returnString = "returnString2";
} else {
throw new IndexOutOfBoundsException("exception >2 ");
}
return returnString;
}
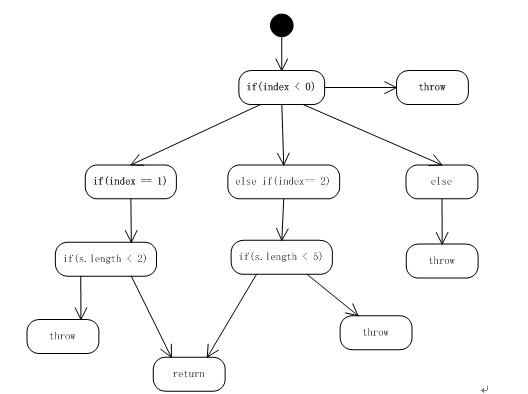
根据公式 V(G) = e – n + 2 = 12 – 8 + 2 = 6 。
case2的圈复杂段为6。
说明一下为什么n = 8，虽然图上的真正节点有12个，
但是其中有5个节点为throw、return，这样的节点为end节点，只能记做一个。
在开发中常用的检测圈复杂度的工具，PMD,checkstyle都可以检测到高复杂度的代码块。
在代码的开发中，配合各种圈复杂度的检测插件，将高复杂度的代码进行适当的拆分、优化，可以大大提高代码整体的质量，减少潜在bug存在。
