7-30-组队赛
链接:http://acm.hust.edu.cn/vjudge/contest/view.action?cid=27642#overview
这一次是二分、三分全场.............也是本人我第一次做这类的题目.......虽然如此但感觉还不错.....
这次的组队赛名次与上次持平,但AC个数与第一名相同,只是时间多了......总体来说有进步~嗯~队友给力啊~~
A.POJ 1905 Expanding Rods
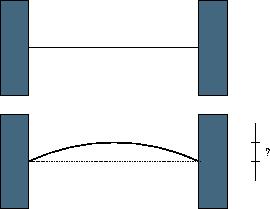
给出了弧长L和弧长两端的直线l距离,求弧长和直线的最大距离~
采用二分求圆的半径,在l/2和一个代入式子中能使L'小于所给的L的半径之间二分求取合适的半径r(L'=r*2*arcsin(l/(2*r))),再用式子r-sqrt(r^2-l^2/4)求H的长度。
代码如下(队友):
1 #include<iostream> 2 #include<stdio.h> 3 #include<algorithm> 4 #include<math.h> 5 using namespace std; 6 double l; 7 double f(double a) 8 { 9 return 2*asin(l/(a*2))*a; 10 } 11 double g(double b) 12 { 13 return b-sqrt(b*b-l*l/4); 14 } 15 int main() 16 { 17 double n,c,r1,r2,L,mid; 18 while(scanf("%lf%lf%lf",&l,&n,&c)!=EOF) 19 { 20 if(l<0&&n<0&&c<0) 21 break; 22 if(l==0||n==0||c==0) 23 {printf("0.000\n");continue;} 24 r1=l/2; 25 r2=l; 26 L=(1+n*c)*l; 27 while(f(r2)>L) 28 r2=r2*2; 29 while(fabs(f(r1)-f(r2))>1e-9) 30 { 31 mid=r1/2+r2/2; 32 if(f(mid)>L) 33 r1=mid; 34 else if(f(mid)<L) 35 r2=mid; 36 else 37 break; 38 } 39 printf("%.3lf\n",g(mid)); 40 } 41 return 0; 42 }
B.POJ 2002 Squares
链接: Squares
C.POJ 2456 Aggressive cows
这题是我做的,磨了很久啊..........刚开始没有思路,后来有思路了,又在怎么使二分长度的时候跳出卡了很久,还WA了一次..........= =
思路:
因为是求最大的最小距离(最大是指要把牛完全放进仓库里使牛相互之间的距离尽可能的最大)(最小是指:在这些相互之间的距离中最小的是多少),显然,距离绝不会超过最大仓库与最小仓库之间的距离L。所以用二分法求最大的最小距离,在0~L之间二分。
代码如下:
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 using namespace std; 5 6 int N,C,a[1000000]; 7 8 int juge(int m) //判断该长度是比所求长度大了还是小了 9 { 10 int number=1,i,frontt=0; 11 for(i=0;i<N;i++) 12 { 13 if((a[i]-a[frontt])>=m) 14 { 15 frontt=i; 16 number++; 17 if(number==C) return 1; //能把牛全部放进仓库,该长度m<=所求长度 18 } 19 } 20 return 0; //不能把牛全部放进仓库,该长度m>所求长度 21 } 22 23 int main() 24 { 25 int i,midd,left,right; 26 scanf("%d%d",&N,&C); 27 for(i=0;i<N;i++) 28 scanf("%d",&a[i]); 29 sort(a,a+N); 30 left=0; 31 right=a[N-1]-a[0]; 32 while(left<=right) //这一段的循环是重点!!!因为一定会有一个整数输出,不存在精度的问题,跳出就无法用精度判断!!!而是使用左右点判断!!! 33 { 34 midd=(left+right)/2; 35 if(juge(midd)) 36 left=midd+1; //+1和-1是为了使left>right的情况存在,使循环结束;若没有+1和-1则无法使循环结束。 37 else 38 right=midd-1; 39 } 40 printf("%d\n",right); //循环结束时,正好left比所求点大1,right就为所求点 41 return 0; 42 }
D.HDU 2141 Can you find it?
同样采用二分,不过有三组数,因此先合并两组做一组数hebin[],在和另一组c[]一起处理.hebin[]=x[i]-c[],二分hebin[]组,看是否能在hebin[]找出符合式子的值。
代码:
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 7 int a[510],b[510],c[510],hebin[250010],x[1010]; 8 int A,B,C,X; 9 10 int juge(int key) //判断在hebin[]是否有符合式子的值~ 11 { 12 int left,right,midd,i; 13 left=0; 14 right=A*B-1; 15 while(left<=right) 16 { 17 midd=(left+right)/2; 18 if(hebin[midd]<=key) 19 left=midd+1; 20 else 21 right=midd-1; 22 } 23 if(right<0 || right>A*B-1) return 0; //注:有可能该值其实超出了hebin[]的范围,那么right有可能会为-1,因此单独返回0; 24 if(hebin[right]==key) return 1; 25 else return 0; 26 } 27 28 int main() 29 { 30 int ii=0; 31 while(scanf("%d%d%d",&A,&B,&C)!=EOF) 32 { 33 ii++; 34 int i,j,h,p; 35 for(i=0;i<A;i++) 36 scanf("%d",&a[i]); 37 for(i=0;i<B;i++) 38 scanf("%d",&b[i]); 39 for(i=0;i<C;i++) 40 scanf("%d",&c[i]); 41 scanf("%d",&X); 42 for(i=0;i<X;i++) 43 scanf("%d",&x[i]); 44 printf("Case %d:\n",ii); 45 for(i=0,h=0;i<A;i++) //我是把前两组进行合并~ 46 for(j=0;j<B;j++) 47 hebin[h++]=a[i]+b[j]; 48 sort(hebin,hebin+A*B); 49 for(i=0;i<X;i++) 50 { 51 p=0; 52 for(j=0;j<C;j++) 53 if(juge(x[i]-c[j])){p=1; break;} 54 if(p==1) printf("YES\n"); //p=1表示至少有一种方式能凑出xi 55 else printf("NO\n"); 56 } 57 58 } 59 return 0; 60 }
E.HDU 2199 Can you solve this equation?
我想这是最简单和最基础的二分了吧~
代码:
1 #include<stdio.h> 2 #include<math.h> 3 int main() 4 { 5 int y,T; 6 scanf("%d",&T); 7 while(T--) 8 { 9 double l=0,r=100,mid,sum; 10 scanf("%d",&y); 11 if(y<6||y>807020306) 12 { 13 printf("No solution!\n"); 14 continue; 15 } 16 while(r-l>1e-9) 17 { 18 mid=(r+l)/2; 19 sum=pow(mid,4)*8+7*pow(mid,3)+mid*mid*2+3*mid+6; 20 if(sum>y) 21 r=mid; 22 else if(sum<y) 23 l=mid; 24 else if(sum==y) 25 break; 26 } 27 printf("%.4lf\n",mid); 28 } 29 return 0; 30 }
(小夕的代码.......然后呢~嘻嘻~是我改正的........错在了让人很无语的地方......= =)
F.HDU 2899 Strange fuction
用三分的方法,小夕童鞋用了二分(求导,然后所求极值点即所求的x值,代入F(x)中得到所求值)答案很接近但还是不对~
我想了一下觉得,用二分,是用F(x)的导函数求得的,因为本来求得的值就有很大误差,而这个误差是在导函数的范围内并不是原函数的,而题目所给的精度应该是满足原函数而不是导函数。因此把有误差的x代入原函数中,所求的值的误差会扩大!!!!因此用二分求得的值很接近应得值,但是绝不是应得值!!!
代码:
1 #include<iostream> 2 #include<stdio.h> 3 #include<algorithm> 4 #include<math.h> 5 using namespace std; 6 double y; 7 double dis(double x) 8 { 9 return 6*pow(x,7)+8*pow(x,6)+7*pow(x,3)+5*x*x-y*x; 10 } 11 int main() 12 { 13 double left,right,mid,mmid,t2,t1; 14 int t; 15 scanf("%d",&t); 16 while(t--) 17 { 18 mid=1;mmid=0; 19 scanf("%lf",&y); 20 left=0;right=100; 21 while(fabs(mid-mmid)>1e-9) 22 { 23 mid=left/2+right/2; 24 mmid=mid/2+right/2; 25 t2=dis(mid);t1=dis(mmid); 26 if(t2>t1) 27 { 28 left=mid; 29 } 30 else if(t2<t1) 31 { 32 right=mmid; 33 } 34 else 35 break; 36 } 37 printf("%.4lf\n",t1); 38 } 39 return 0; 40 }
G.HDU 2298 Toxophily
我采用的是数学方法做的,代码很短~~链接:Toxophily
H.HDU 4355 Party All the Time
三分~
代码:
1 #include<stdio.h> 2 #include<string.h> 3 #include<stdlib.h> 4 double ab(double x) 5 { 6 return x>0?x:-x; 7 } 8 struct node 9 { 10 double x; 11 double w; 12 }q[50005]; 13 int n; 14 double cal(double xi) 15 { 16 int i; 17 double res=0; 18 for(i=0;i<n;i++) 19 { 20 double t=ab(q[i].x-xi); 21 res+=t*t*t*q[i].w; 22 } 23 return res; 24 } 25 int main() 26 { 27 int ca=1,i,t; 28 double l,r,m,mm,ans; 29 scanf("%d",&t); 30 while(t--) 31 { 32 scanf("%d",&n); 33 for(i=0;i<n;i++) 34 scanf("%lf%lf",&q[i].x,&q[i].w); 35 l=q[0].x; 36 r=q[n-1].x; 37 while(l<r) 38 { 39 if(ab(r-l)<=0.001) 40 break; 41 m=(l+r)/2; 42 mm=(m+r)/2; 43 if(cal(m)<cal(mm)) 44 { 45 ans=cal(m); 46 r=mm; 47 } 48 else l=m; 49 } 50 printf("Case #%d: ",ca++); 51 printf("%.0lf\n",ans); 52 } 53 return 0; 54 }




