POJ - 1062 昂贵的聘礼(抽象转化最短路)

题目大意

你想娶酋长的女儿，但酋长要求你给一定数额金钱的聘礼。除了金钱外，酋长也允许你用部落里其他人的某物品加上一点钱作为聘礼。而其他人的物品也可以通过指定的另外一些人的某物品加上一些金钱获得。部落里的每个人有一个等级。你的整个交易过程涉及的人的等级只能在一个限定的差值内。问你最少需要多少金钱才能娶到酋长女儿。假定每个人只有一个物品。

输入

输入第一行是两个整数M，N（1 <= N <= 100），依次表示地位等级差距限制和物品的总数。接下来按照编号从小到大依次给出了N个物品的描述。每个物品的描述开头是三个非负整数P、L、X（X < N），依次表示该物品的价格、主人的地位等级和替代品总数。接下来X行每行包括两个整数T和V，分别表示替代品的编号和"优惠价格"。

输出

输出最少需要的金币数。

样例

input:
1 4
10000 3 2
2 8000
3 5000
1000 2 1
4 200
3000 2 1
4 200
50 2 0

output:
5250

分析

整个交换是一个连续的过程, 要求得最小的花费可转化成求在最短路的问题.
求最短路问题需要有起点, 终点, 路权这三个要素, 下面进行进一步的抽象:
以样例为例:
只考虑路权 不考虑等级差距等:

考虑直接购买每个物品的支出:

由于每个点都可以作为起点 且直接购买某一物品的花费也需要表示为权值, 故创建虚拟原点进一步转化:

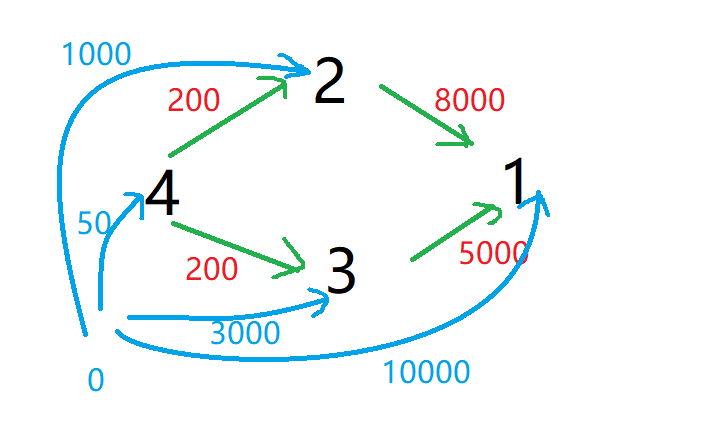
很显然最短路是0->4->3->1 费用为50 + 200 + 5000 = 5250
这样, 直接购买某个物品的花费也转化为路权,
接下来求出从0点到1点的最短路即可.
同时, 考虑身份地位带来的影响, Dijkstra更新点时只能更新等级差距限制范围内的点.
遍历区间 [酋长的地位-m, 酋长的地位], 每次Dijkstra区间范围都在[i, i+m], 所求最小答案为解

完整代码如下:

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
const int N = 1010, INF = 0x3f3f3f3f;
int n, m;
int g[N][N], level[N];
int dist[N];
bool st[N];

int dijkstra(int down, int up) {
    memset(dist, 0x3f, sizeof dist);
    memset(st, 0, sizeof st);

    dist[0] = 0;
    for(int i = 1; i <= n; i++) {
        int t = -1;
        for(int j = 0; j <= n; j++)
            if(!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
        st[t] = 1;
        for(int j = 1; j <= n; j++)
            if(down <= level[j] && level[j] <= up)
                dist[j] = min(dist[j], dist[t] + g[t][j]);
    }
    return dist[1];
}

int main() {
    scanf("%d%d", &m, &n);
    memset(g, 0x3f, sizeof g);
    for(int i = 1; i <= n; i++) g[i][i] = 0;

    for(int i = 1; i <= n; i++) {
        int p, x; scanf("%d%d%d", &p, &level[i], &x);
        g[0][i] = min(p, g[0][i]);
        while(x--) {
            int id, cost;
            scanf("%d%d", &id, &cost);
            g[id][i] = min(g[id][i], cost);
        }
    }
    int res = INF;
    for(int i = level[1] - m; i <= level[1]; i++) res = min(res, dijkstra(i, i + m));
    printf("%d\n", res);
}