SP1716 GSS3 - Can you answer these queries III (线段树维护最大连续子段和)

题目大意:

    给定数列A以及M条指令      "1 x y" 查询[x, y]中的最大连续子段和 "2 x y"把A[x] 改成y

单点修改的操作不再赘述 对于维护最大连续子段和的思路如下:

先从二叉树的视角考虑一下线段树中所有的情况:

tmax为最大连续子段和 最大前缀和为lmax 最大后缀和为rmax

1. 只需要递归左子区间或只需要递归右子区间

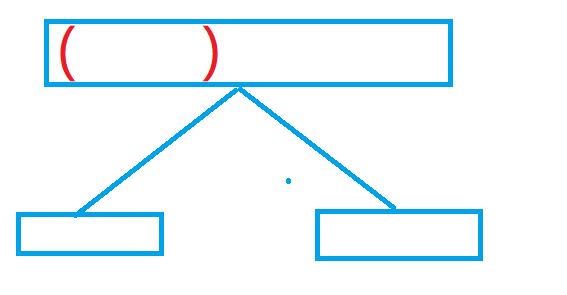
tmax = max (tmax, left_son)

 

 tmax = max(tmax, right_son)

 2.区间横跨mid(不与端点重合)时, 则需要同时递归左右子区间

此时还需维护左子区间的最大后缀和以及右子区间的最大前缀和

此时横跨左右子区间的最大子段和 = 左子区间的最大后缀和 + 右子区间的最大前缀和

 

tmax = max(tmax, left_son.rmax + right_son.lmax)

3.计算前缀/后缀

 

 tmax = max(tmax, left_son.sum + right_son.lmax)

4.完全覆盖该区间

　　直接返回即可

 由此可知 线段树结构体中需要维护端点信息l和r,  最大前缀和lmax 最大后缀和rmax 当前区间和sum

线段树思想中有一点很关键, 就是要找到所有需要维护的信息应对各个情况, 需要让结构体中的信息具有完备性

查询时为了简化操作 用pushup更新并返回结构体

完整代码如下:

/*
 * @Author: Hellcat
 * @Date: 2020-03-10 14:15:14
 */
#include <bits/stdc++.h>
using namespace std;

const int N = 5e4 + 10;

int n, m, a[N];
struct node {
    int l, r;
    int tmax; // 最大连续子段和
    int lmax; // 最大前缀和
    int rmax; // 最大后缀和
    int sum;  // 区间[l, r]中的最大值
}tr[N<<2];

void pushup(node &u, node &l, node &r) {
    u.sum = l.sum + r.sum;
    u.lmax = max(l.lmax, l.sum + r.lmax);
    u.rmax = max(r.rmax, r.sum + l.rmax);
    u.tmax = max(max(l.tmax, r.tmax), l.rmax + r.lmax);
}

void pushup(int u) {
    pushup(tr[u], tr[u<<1], tr[u<<1 | 1]);
}

void build(int u, int l, int r) {
    tr[u] = {l, r, a[r], a[r], a[r], a[r]};
    if(l == r) return;
    int mid = (l + r) >> 1;
    build(u<<1, l, mid);
    build(u<<1 | 1, mid + 1, r);
    pushup(u);
}

void modify(int u, int x, int v) {
    if(tr[u].l == tr[u].r) { tr[u] = {x, x, v, v, v, v}; return; }
    int mid = (tr[u].l + tr[u].r) >> 1;
    if(x <= mid) modify(u << 1, x, v);
    else modify(u << 1 | 1, x, v);
    pushup(u);
}

node query(int u, int l, int r) {
    if(l <= tr[u].l && tr[u].r <= r) return tr[u];
    int mid = (tr[u].l + tr[u].r) >> 1;
    if(r <= mid) return query(u << 1, l, r);
    if(l > mid) return query(u << 1 | 1, l, r);
    auto left = query(u << 1, l, r);
    auto right = query(u << 1 | 1, l, r);
    node res;
    pushup(res, left, right);
    return res;
}

int main() {
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
    build(1, 1, n);
    int p; scanf("%d", &p);
    while(p--) {
        int op, x, y;
        scanf("%d%d%d", &op, &x, &y);
        if(op == 0) modify(1, x, y);
        else {
            node res = query(1, x, y);
            printf("%d\n", res.tmax);
        }
    }
}