luogu P1044 火车进出栈问题(Catalan数)

Catalan数就是魔法

火车进出栈问题即:

一个栈（无穷大）的进栈序列为 1,2,3,4,...,n 求有多少个不同的出栈序列？

将问题进行抽象, 假设'+'代表进栈, 则有'-'代表出栈

那么如果进栈序列为123, 则:

+ + + - - - 将1, 2, 3压入栈后再将3, 2, 1弹出 得到出栈序列为321

同样, + - + - + - 得到出栈序列为123

上面所述的均为合法进出栈的序列 可发现规律: 序列中 + 的个数等于 - 的个数

但是如 + - - + +  - 这样的序列, 在栈为空时仍进行弹出操作的, 为非法序列

进一步将 + - 序列抽象到平面直角坐标系中, + 代表向右走一格, -代表向上走一格, 可知y = x直线下方的序列均为合法序列, 如下图所示:

 

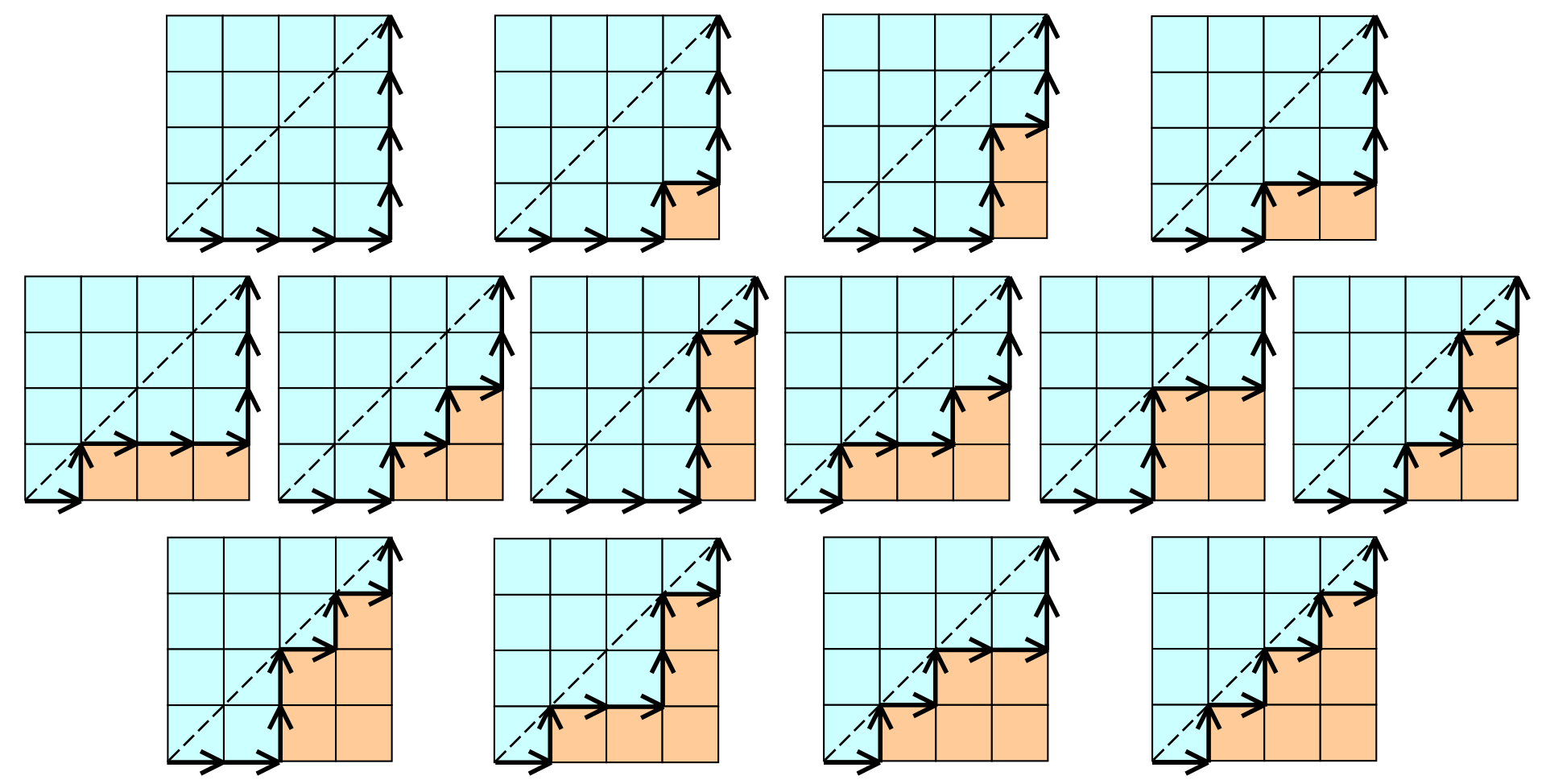
到这里, 火车进出栈问题就已经抽象为非降路径(只能向上走或向右走的路径)的问题

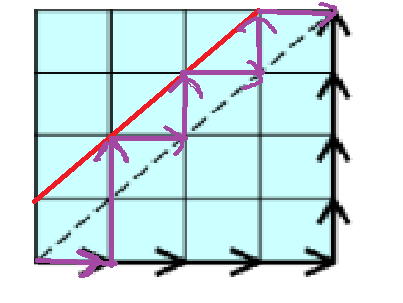
对于路径计数问题:

1)从(0,0)到(n,n)的非降路径等于n个x和n个y的排列数 即路径数为C(2n, n);

2)如果不是合法序列, 则会经过上图中的红线, 不合法序列一定会经过点(n -1, n), 从(0, 0)到(n -1, n)有C(2n, 2n-1)种不合法的路径;

3)综合1), 2) 并依据组合数性质化简

推导出公式:

 

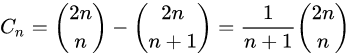
我们可以得到出栈序列的总数为C(2n, n) / (n + 1).

下面以luogu P1044 栈为例, 完整代码如下:

/*
 * @Author: Hellcat
 * @Date: 2020-02-27 15:54:37
 */
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

ll C(int n, int m) {
    ll ans = 1;
    for(ll i = 1; i <= m; i++)
        ans = ans * (n - m + i) / i;
    return ans;
}

int main() {
    int n;
    scanf("%d", &n);
    printf("%lld\n", C(2*n, n) / (n + 1));
}

题给数据量不大 选择高效的组合数计算方法即可 无需高精度算法.

同时给出完全模拟的dfs暴力搜索算法如下:

dfs时候需要注意 为保证字典序输出优先考虑出栈.

#include <bits/stdc++.h>
using namespace std;

int n, cnt = 20;
vector<int> state1;
stack<int> state2;
int state3 = 1;

int res = 0;

void dfs() {
    if(!cnt) return;
    if(state1.size() == n) {
        res++;
        cnt--;
        for(auto x : state1) cout<<x;
        puts("");
        return;
    }
    // 按字典序输出 则出栈先
    if(state2.size()) { // 出栈
        state1.push_back(state2.top());
        state2.pop();
        dfs();
        state2.push(state1.back()); // 回溯
        state1.pop_back();
    }
    if(state3 <= n) { // 入栈
        state2.push(state3);
        state3++;
        dfs();
        state3--; // 回溯
        state2.pop();
    }
}

int main() {
    scanf("%d", &n);
    dfs();
    printf("%d\n", res);
}

输入

3

输出

123
132
213
231
321
5