拓端tecdat|R语言贝叶斯非参数模型：密度估计、非参数化随机效应meta分析心肌梗死数据

原文链接：http://tecdat.cn/?p=23785

原文出处：拓端数据部落公众号

概述

最近，我们使用贝叶斯非参数（BNP）混合模型进行马尔科夫链蒙特卡洛（MCMC）推断。

在这篇文章中，我们通过展示如何使用具有不同内核的非参数混合模型进行密度估计。在后面的文章中，我们将采用参数化的广义线性混合模型，并展示如何切换到非参数化的随机效应表示，避免了正态分布的随机效应假设。

使用Dirichlet Process Mixture模型进行基本密度估计

提供了通过Dirichlet过程混合（DPM）模型进行非参数密度估计的机制（Ferguson, 1974; Lo, 1984; Escobar, 1994; Escobar and West, 1995）。对于一个独立和相同分布的样本 ，该模型的形式为

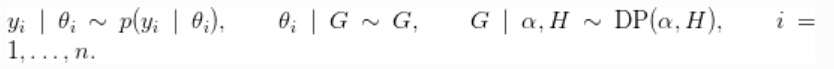
这个模型实现是灵活的，运行任意核的混合。, 可以是共轭的，也可以是不共轭的（也是任意的）基度量 . 在共轭核/基数测量对的情况下，能够检测共轭的存在，并利用它来提高采样器的性能。

为了说明这些能力，我们考虑对R中提供的Faithful火山数据集的喷发间隔时间的概率密度函数进行估计。

data(faithful)

观测值  对应于数据框架的第二列，而 .

使用CRP表示法拟合高斯location-scale 分布混合分布

模型说明

我们首先考虑用混合正态分布的location-scaleDirichlet过程s来拟合转换后的数据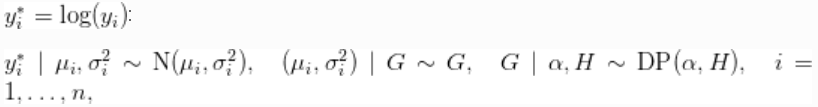

其中 对应的是正态-逆伽马分布。这个模型可以解释为提供一个贝叶斯版本的核密度估计 用于使用高斯核和自适应带宽。在数据的原始尺度上，这可以转化为一个自适应的对数高斯核密度估计。

引入辅助变量，表明混合的哪个成分产生了每个观测值，并对随机量进行积分，我们得到模型的CRP表示（Blackwell and MacQueen, 1973）。

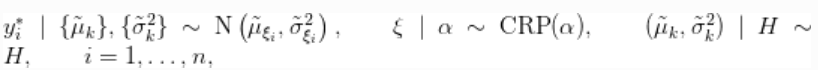
其中

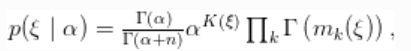
是向量中唯一值的数量，是第个唯一值在中出现的次数。这个说明清楚地表明，每个观测值都属于最多正态分布聚类中的任何一个，并且CRP分布与分区结构的先验分布相对应。

这个模型的说明是这样的

1.  
   y[i] ~ dnorm(mu[i], var = s2[i])
2.  
   mu[i] <- muTilde[xi[i]]
3.  
   s2[i] <- s2Tilde[xi[i]]
4.  
   xi[1:n] ~ dCRP(alpha, size = n)
5.  
   muTilde[i] ~ dnorm(0, var = s2Tilde[i])
6.  
   s2Tilde[i] ~ dinvgamma(2, 1)
7.  
   alpha ~ dgamma(1, 1)

请注意，在模型代码中，参数向量muTilde和s2Tilde的长度被设置为.我们这样做是因为目前的实现要求提前设置参数向量的长度，并且不允许它们的数量在迭代之间变化。因此，如果我们要确保算法总是按预期执行，我们需要在最坏的情况下工作，即有多少个成分就有多少个观测值的情况。但它的效率也有点低，无论是在内存需求方面（当 规模大时，需要维护大量未占用的成分）还是在计算负担方面（每次迭代都需要更新大量不需要后验推理的参数）。当我们在下面使用伽马分布的混合时，我们将展示一个能提高效率的计算捷径。

还需要注意的是，的值控制着我们先验预期的成分数量，的值越大，对应于数据占据的成分数量越多。因此，通过指定一个先验值，我们为模型增加了灵活性。对Gamma先验的特殊选择允许使用数据增强方案从相应的全条件分布中有效取样。也可以选择其他的先验，在这种情况下，这个参数的默认采样是一个自适应的随机游走Metropolis-Hastings算法。

运行MCMC算法

下面的代码设置了数据和常数，初始化了参数，定义了模型对象，并建立和运行了MCMC算法。默认采样器是一个折叠的吉布斯采样器（Neal, 2000）。

1.  
    
2.  
   # 模型数据
3.  
   y = standlFaithful
4.  
   # 模型常量
5.  
   n = length(standlFaithful))
6.  
   # 参数初始化
7.  
   list(xi = sample(1:10, size=n, replace=TRUE),
8.  
   # 创建和编译模型
9.  
   Model(code, data, inits, consts)
10.  
    ##定义模型...
11.  
    ##建立模型...
12.  
    ##设置数据和初始值...
13.  
    ##在模型上运行计算（随后的任何错误报告可能只是反映了模型变量的缺失值）...
14.  
    ##检查模型的大小和尺寸......。
15.  
    ##模型构建完成。
16.  
    ## 编译完成。
17.  
    #MCMC的配置、创建和编译
18.  
    MCMC(conf)
19.  
    ## 编译......这可能需要一分钟
20.  
    ## 编译完成。
21.  
     

 

我们可以从参数的后验分布中提取样本，并创建痕迹图、直方图和任何其他感兴趣的总结。例如，对于参数，我们有。
 

1.  
   # 参数的痕迹图
2.  
   ts.plot(samples[ , "alpha"], xlab = "iteration", ylab = expression(alpha))

1.  
    
2.  
   # 后验直方图
3.  
   hist(samples[ , "alpha"], xlab = expression(alpha), main = "", ylab = "Frequency")
4.  
    

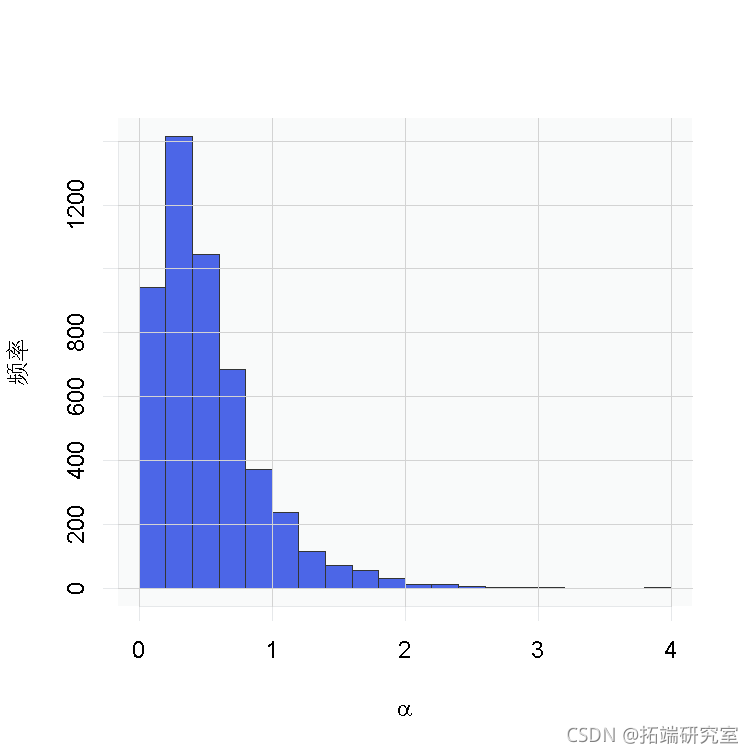
在这个模型下，对于一个新的观察，后验预测分布是最佳密度估计（在平方误差损失下）。这个估计的样本可以很容易地从我们的MCMC产生的样本中计算出来。

1.  
    
2.  
   # 参数的后验样本
3.  
   samples[, "alpha"]
4.  
   # 平均值的后验样本
5.  
   samples[, grep('muTilde', colnames(samples))] # 聚类平均数的后验样本。
6.  
   # 集群方差的后验样本
7.  
   samples[, grep('s2Tilde', colnames(samples))] # 聚类成员的后验样本。
8.  
   # 聚类成员关系的后验样本
9.  
   samples [, grep('xi', colnames(samples))] # 聚类成员的后验样本。
10.  
     
11.  
    hist(y, freq = FALSE,
12.  
    xlab = "标准化对数尺度上的等待时间")
13.  
    ##对标准化对数网格的密度进行点式估计
14.  
     

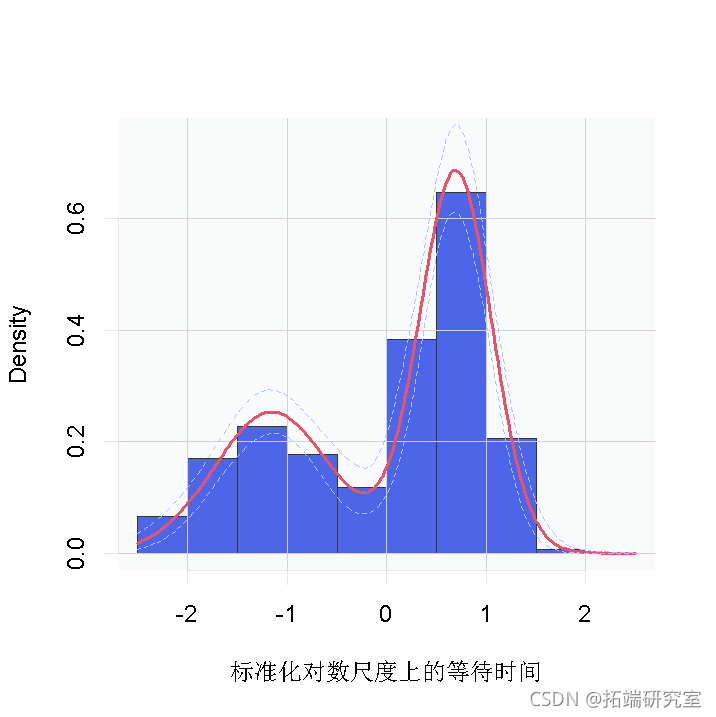
然而，回顾一下，这是对等待时间的对数的密度估计。为了获得原始尺度上的密度，我们需要对内核进行适当的转换。 

1.  
   standlGrid*sd(lFaithful) + mean(lFaithful) # 对数尺度上的网格
2.  
    
3.  
   hist(faithful$waiting, freq = FALSE
4.  
    

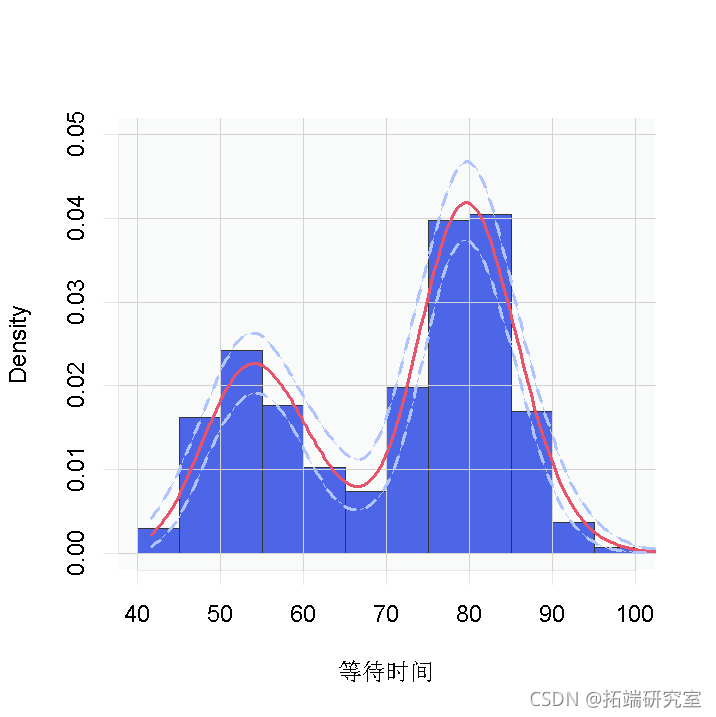
无论是哪种情况，都有明显的证据表明，数据中的等待时间有两个组成部分。

生成混合分布的样本

虽然混合分布的线性函数的后验分布的样本（比如上面的预测分布）可以直接从折叠采样器的实现中计算出来，但是对于非线性函数的推断需要我们首先从混合分布中生成样本。我们可以从随机度量中获得后验样本。需要注意的是，为了从 ，得到后验样本，我们需要监控所有参与其计算的随机变量，即成员变量xi，聚类参数muTilde和s2Tilde，以及浓度参数alpha。

下面的代码从随机测量中生成后验样本。cMCMC对象包括模型和参数的后验样本。函数估计了一个截断水平，即truncG。后验样本是一个带列的矩阵，其中参数分布向量的维度（在本例中为）。

outputG <- getSamplesDPmeasure(cmcmc)

下面的代码使用随机测量的后验样本来计算的后验样本。请注意，这些样本是基于转换后的模型计算的，大于70的值对应于上述定义的网格上大于0.035的值。

1.  
    
2.  
   truncG <- outputG$trunc # G的截断水平
3.  
    
4.  
    
5.  
    
6.  
   probY70 <- rep(0, nrow(samples)) # P(y.tilde>70)的后验样本
7.  
    
8.  
   hist(probY70 )
9.  
    

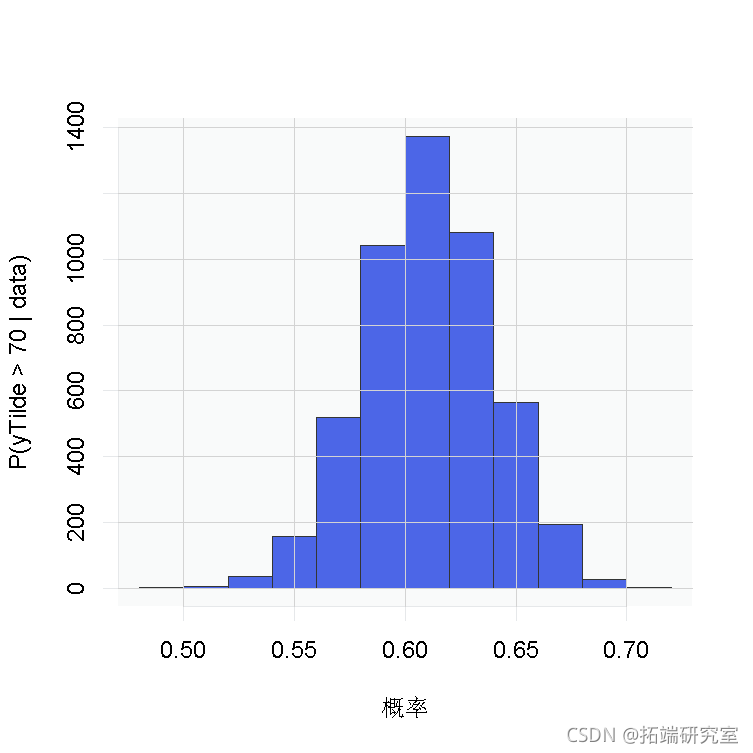
使用CRP表示法拟合伽马混合分布

不限于在DPM模型中使用高斯核。就Old Faithful数据而言，除了我们在上一节中介绍的对数尺度上的高斯核的混合分布外，还有一种选择是数据原始尺度上的伽马混合分布。

模型

在这种情况下，模型的形式为

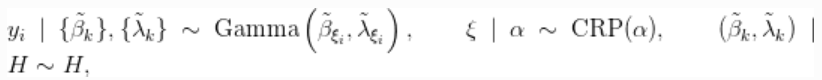
其中对应于两个独立Gamma分布的乘积。下面的代码提供了该模型。

1.  
   y[i] ~ dgamma(shape = beta[i], scale = lambda[i])
2.  
   beta[i] <- betaTilde[xi[i]]
3.  
   lambda[i] <- lambdaTilde[xi[i]]

请注意，在这种情况下，向量beta和lambda的长度为 。这样做是为了减少与采样算法有关的计算和存储负担。你可以把这种方法看作是对过程的截断，只不过它可以被认为是*精确的截断。事实上，在CRP表示法下，只要采样器的成分数严格低于采样器每次迭代的参数向量的长度，使用长度短于样本中观察值的参数向量就会生成一个合适的算法。

运行MCMC算法

下面的代码设置了模型数据和常数，初始化了参数，定义了模型对象，并建立和运行了Gamma混合分布的MCMC算法。请注意，在构建MCMC时，会产生一个关于聚类参数数量的警告信息。这是因为betaTilde和lambdaTilde的长度小于。另外，请注意，在执行过程中没有产生错误信息，这表明所需的集群数量未超过50个的上限。

1.  
   data <- list(y = waiting)
2.  
   Model(code, data = data)

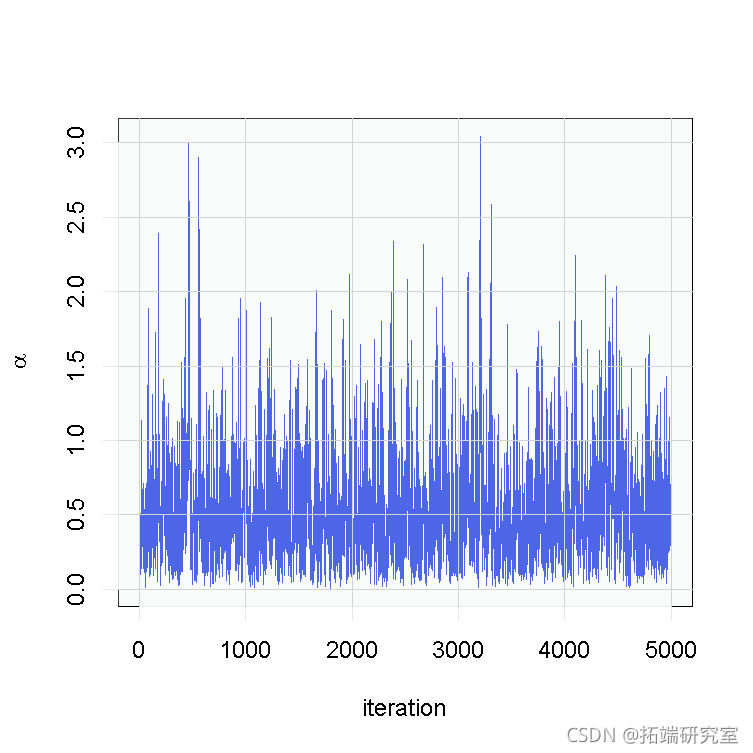
cModel <- compile

samples <- runMCMC(cmcmc, niter = 7000, nburnin = 2000, setSeed = TRUE)

在这种情况下，我们使用参数的后验样本来构建一个轨迹图，并估计的后验分布。
 

1.  
   # 参数的后验样本的跟踪图
2.  
   ts.plot(samples[ , 'alpha'], xlab = "iteration", ylab = expression(alpha))

1.  
    
2.  
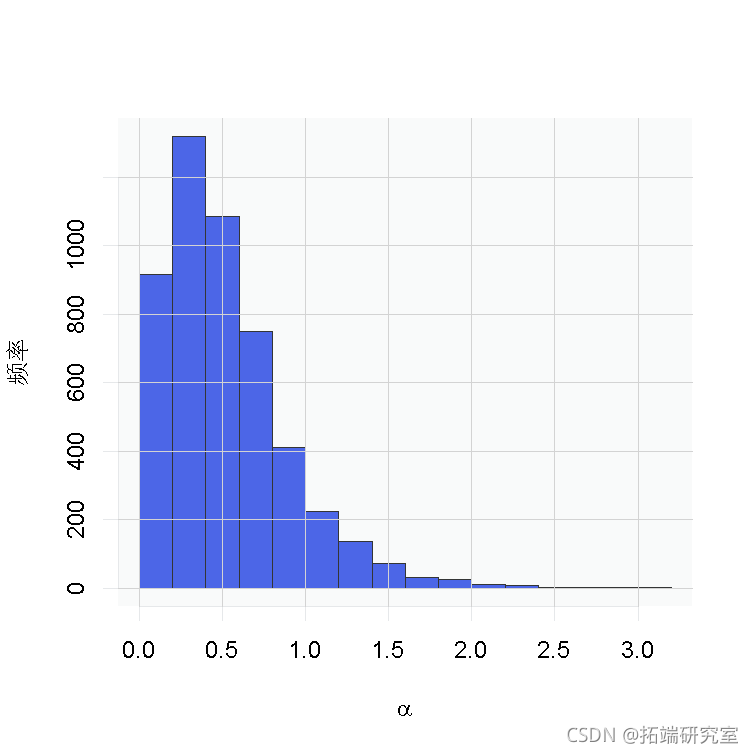
   # 参数的后验样本的直方图
3.  
   hist(samples[, 'alpha'])
4.  
    

从混合分布中生成样本

和以前一样，我们从后验分布中获得样本。
 

outputG <- getSamplesDPmeasure(cmcmc)

我们使用这些样本来创建一个数据密度的估计值，以及一个95%置信带。 

1.  
    
2.  
   for(iter in seq_len)) {
3.  
   density[iter, ] <- sapply(grid, function(x)
4.  
   sum( weightSamples[iter, ] * dgamma)))
5.  
   }
6.  
    
7.  
    
8.  
   hist(waiting, freq = FALSE
9.  
    

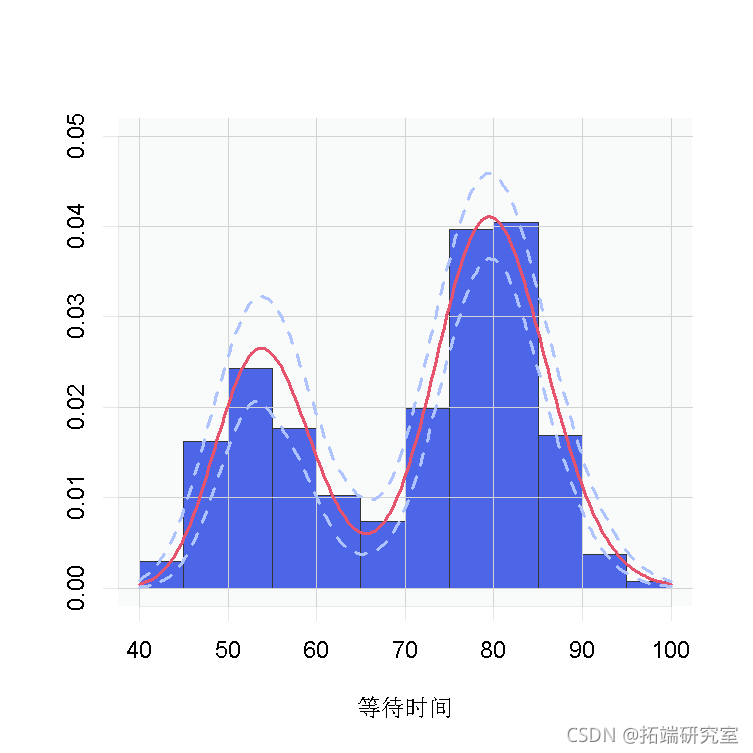
我们再次看到，数据的密度是双峰的，看起来与我们之前得到的数据非常相似。

使用stick-breaking 表示法拟合伽马DP混合分布

模型

Dirichlet过程混合物的另一种表示方法是使用随机分布的stick-breaking表示（Sethuraman, 1994）。

引入辅助变量，表明哪个成分产生了每个观测值，上一节讨论的Gamma密度的混合物的相应模型的形式为

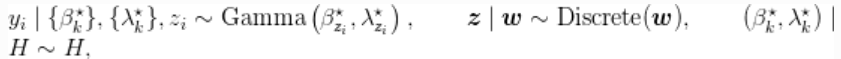
其中 是两个独立Gamma分布的乘积。

与. 下面的代码提供了该模型说明。 

1.  
    
2.  
   y[i] ~ dgamma(shape = beta[i], scale = lambda[i])
3.  
   beta[i] <- betaStar[z[i]]
4.  
   lambda[i] <- lambdaStar[z[i]]
5.  
   z[i] ~ dcat(w[1:Trunc])
6.  
   # stick-breaking
7.  
   v[i] ~ dbeta(1, alpha)
8.  
   w[1:Trunc] <- stick_breaking(v[1:(Trunc-1)]) # stick-breaking 权重
9.  
   betaStar[i] ~ dgamma(shape = 71, scale = 2)

注意，截断水平已被设置为Trunc值，该值将在函数的常数参数中定义。

运行MCMC算法

下面的代码设置了模型数据和常量，初始化了参数，定义了模型对象，并建立和运行了Gamma混合分布的MCMC算法。当使用stick-breaking表示时，会指定一个分块Gibbs抽样器（Ishwaran, 2001; Ishwaran and James, 2002）。

1.  
   data <- list(y = waiting)
2.  
   consts <-length(waiting)
3.  
   betaStar = rgamma
4.  
   lambdaStar = rgamma
5.  
   v = rbeta
6.  
   z = sample
7.  
   alpha = 1
8.  
    

compile(Model)

1.  
   MCMC(rModel, c("w", "betaStar", "lambdaStar", 'z', 'alpha'))
2.  
   comp(mcmc )

MCMC(cmcmc, niter = 24000)

使用stick-breaking近似法会自动提供随机分布的近似值，即 。下面的代码使用来自样本对象的后验样本计算后验样本，并从中计算出数据的密度估计。

1.  
    
2.  
   densitySamples[i, ] <- sapply(grid, function(x) sum(weightSamples * dgamma(x, shape ,
3.  
   scale )))
4.  
    
5.  
   hist( waiting ylim=c(0,0.05),
6.  
    

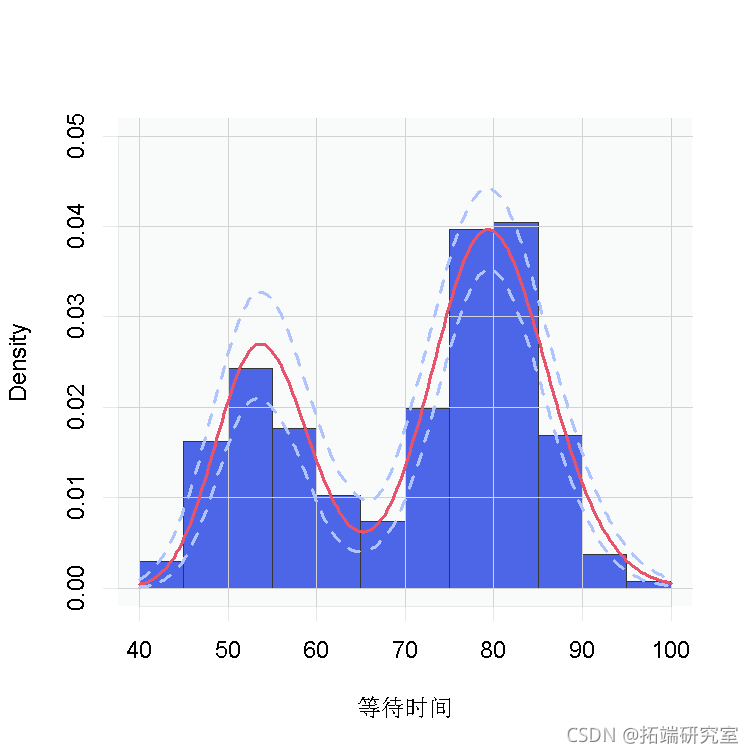
正如预期的那样，这个估计值看起来与我们通过CRP表示的过程获得的估计值相同。

贝叶斯非参数化：非参数化随机效应

我们将采用一个参数化的广义线性混合模型，并展示如何切换到非参数化的随机效应表示，避免了正态分布的随机效应假设。

心肌梗死（MIs）的参数化meta分析

我们将在对以前非常流行的糖尿病药物 "Avandia "的副作用进行meta分析的背景下，说明使用非参数混合模型对随机效应分布进行建模。我们分析的数据在引起对这种药物的安全性的严重质疑方面发挥了作用。问题是使用"Avandia "是否会增加心肌梗死（心脏病发作）的风险。，每项研究都有治疗和对照组。

模型的制定

我们首先进行基于标准的广义线性混合模型（GLMM）的meta分析。向量n和x分别包含对照组的患者总数和每项研究中对照组的心肌梗死患者人数。同样，向量m和y包含接受药物的病人的类似信息。该模型的形式为

其中，随机效应、遵循共同的正态分布、和被合理地赋予非信息性先验。参数量化了对照组和治疗组之间的风险差异，而参数则量化了研究的具体变化。

这个模型可以用以下代码指定。

1.  
    
2.  
   y[i] ~ dbin(size = m[i], prob = q[i]) # 药物MIs
3.  
   x[i] ~ dbin(size = n[i], prob = p[i]) # 控制MIs
4.  
   q[i] <- expit(theta + gamma[i]) # 药物的对数指数
5.  
   p[i] <- expit(gamma[i]) #对照组对数
6.  
   gamma[i] ~ dnorm(mu, var = tau2) # 研究效果
7.  
   theta ~ dflat() # 药物的影响
8.  
   # 随机效应超参数
9.  
   mu ~ dnorm(0, 10)
10.  
    tau2 ~ dinvgamma(2, 1)
11.  
     

运行MCMC

让我们来运行一个基本的MCMC。

1.  
   MCMC(codeParam, data, inits,
2.  
   constants, monitors = c("mu", "tau2", "theta", "gamma")

1.  
   par(mfrow = c(1, 4)
2.  
    
3.  
   hist(gammaMn)
4.  
   hist(samples[1000, gammaCols)

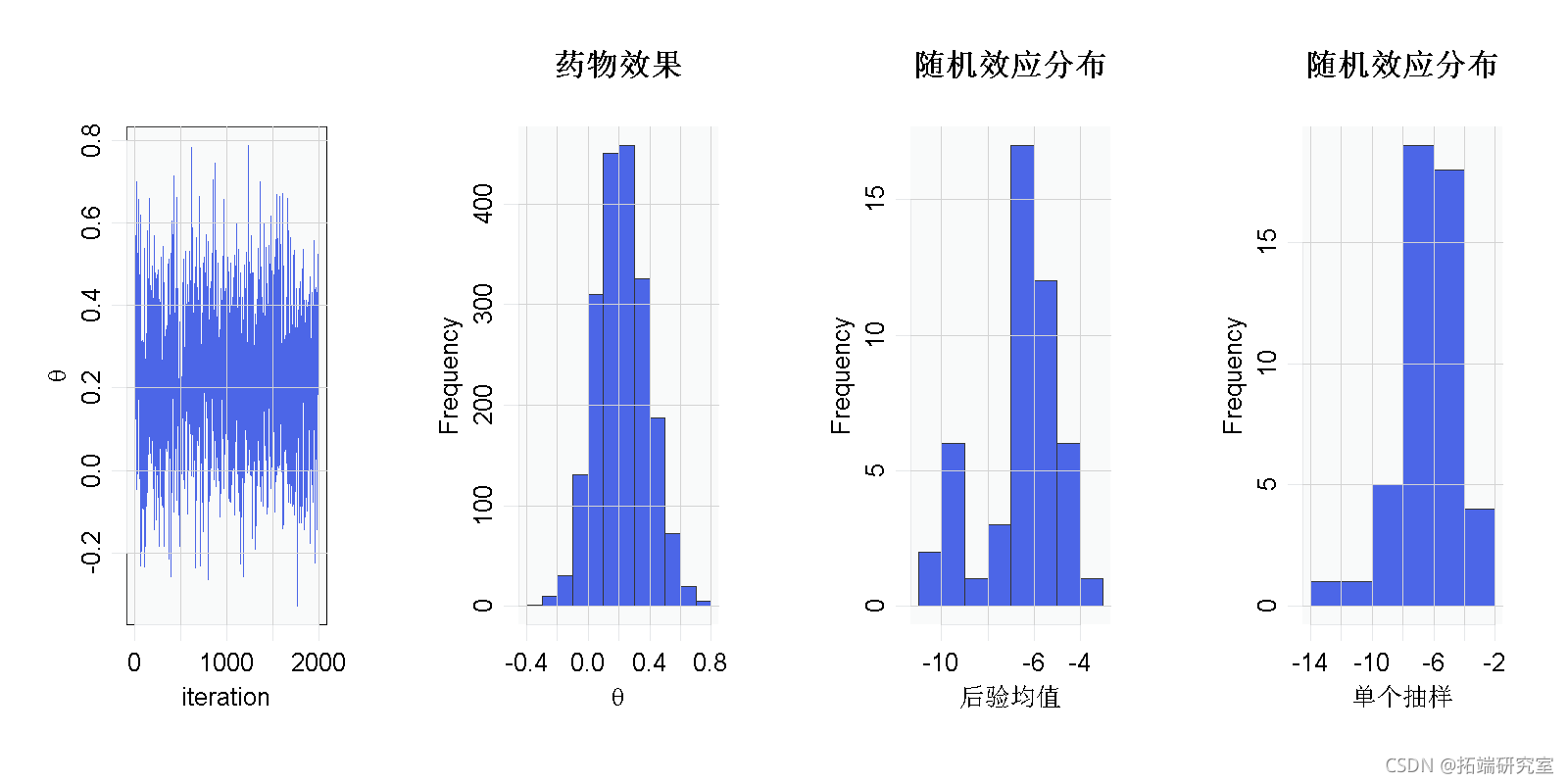
结果表明，对照组和治疗组之间存在着整体的风险差异。但是正态性假设呢？我们的结论对该假设是否稳健？也许随机效应的分布是偏斜的。

用于meta分析的基于DP的随机效应模型

模型

现在，我们对使用非参数分布。更具体地说，我们假设每个都是由位置尺度的正态混合分布产生的。

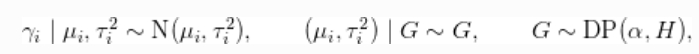
这种模型引起了随机效应之间的聚类。与密度估计问题的情况一样，DP先验允许数据决定分量的数量，从最少的一个分量（即简化为参数模型）到最多的分量，即每个观测值有一个分量。如果数据支持这种行为，这允许随机效应的分布是多模态的，大大增加了其灵活性。这个模型可以用以下代码指定。

1.  
    
2.  
   y[i] ~ dbin(size = m[i], prob = q[i]) # 药物MIs
3.  
   x[i] ~ dbin(size = n[i], prob = p[i]) # MIs
4.  
   q[i] <- expit(theta + gamma[i]) # 药物的对数指数
5.  
   p[i] <- expit(gamma[i]) # 对照组对数值
6.  
   gamma[i] ~ dnorm(mu[i], var = tau2[i]) # 来自混合物的随机效应。
7.  
   mu[i]<- muTilde[xi[i]] # 来自聚类的随机效应的平均值 xi[i]
8.  
   tau2[i] <- tau2Tilde[xi[i]] # 来自群组xi[i]的随机效应变量
9.  
   # 从基础测量中提取混合成分参数
10.  
    muTilde[i] ~ dnorm(mu0, var = var0)
11.  
    tau2Tilde[i] ~ dinvgamma(a0, b0)
12.  
    # 用于将研究报告聚类为混合成分的CRP
13.  
    xi[1:nStudies] ~ dCRP(alpha, size = nStudies)
14.  
    # 超参数
15.  
     
16.  
    theta ~ dflat() # 药物的影响
17.  
     

运行MCMC

以下代码对模型进行了编译，并对模型运行了一个压缩Gibbs抽样

1.  
   inits <- list(gamma = rnorm(nStudies))
2.  
    
3.  
   MCMC(code = BNP, data = data)

1.  
    
2.  
   hist(samplesBNP[, 'theta'], xlab = expression(theta), main = 'avandia的影响')
3.  
   main = "随机效应分布")
4.  
   main = "随机效应分布")
5.  
    
6.  
   # 推断出了多少个混合成分？
7.  
   xiRes <- samplesBNP[, xiCols].
8.  
    

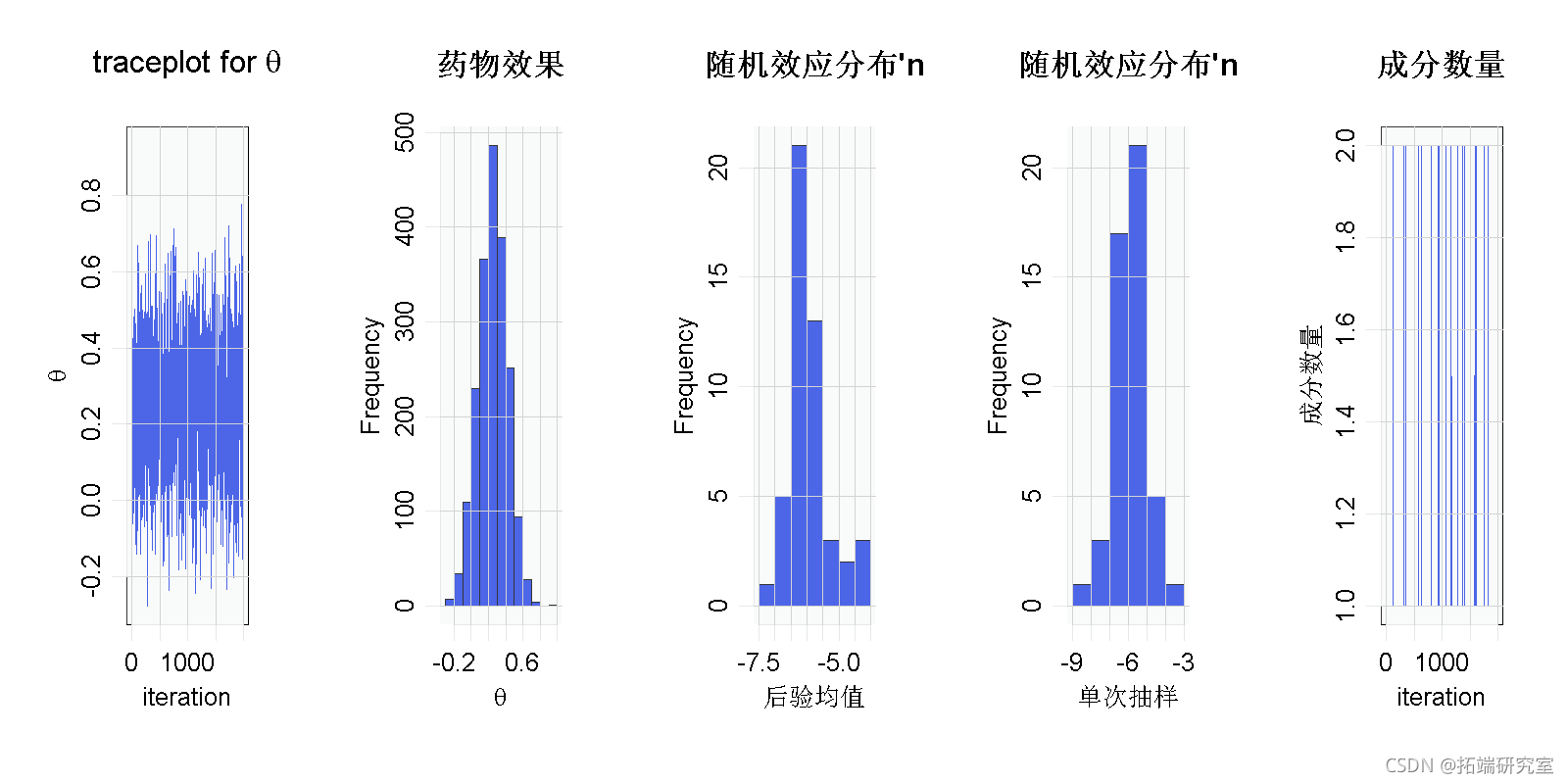
主要推论似乎对原始的参数化假设很稳健。这可能是由于没有太多证据表明随机效应分布中缺乏正态性。

参考文献

Blackwell, D. and MacQueen, J. 1973. Ferguson distributions via Polya urn schemes. The Annals of Statistics 1:353-355.

Ferguson, T.S. 1974. Prior distribution on the spaces of probability measures. Annals of Statistics 2:615-629.

Lo, A.Y. 1984. On a class of Bayesian nonparametric estimates I: Density estimates. The Annals of Statistics 12:351-357.

---

最受欢迎的见解

1.matlab使用贝叶斯优化的深度学习

2.matlab贝叶斯隐马尔可夫hmm模型实现

3.R语言Gibbs抽样的贝叶斯简单线性回归仿真

4.R语言中的block Gibbs吉布斯采样贝叶斯多元线性回归

5.R语言中的Stan概率编程MCMC采样的贝叶斯模型

6.Python用PyMC3实现贝叶斯线性回归模型

7.R语言使用贝叶斯 层次模型进行空间数据分析

8.R语言随机搜索变量选择SSVS估计贝叶斯向量自回归（BVAR）模型

9.matlab贝叶斯隐马尔可夫hmm模型实现