拓端数据tecdat|R语言基于Bagging分类的逻辑回归(Logistic Regression)、决策树、森林分析心脏病患者

原文链接：http://tecdat.cn/?p=22448

原文出处：拓端数据部落公众号

今天，我们将看下bagging 技术里面的启发式算法。

通常，bagging 与树有关，用于生成森林。但实际上，任何类型的模型都有可能使用bagging 。回顾一下，bagging意味着 "boostrap聚合"。因此，考虑一个模型m：X→Y。让表示从样本中得到的m的估计

现在考虑一些boostrap样本，，i是从{1,⋯,n}中随机抽取的。基于该样本，估计。然后抽出许多样本，考虑获得的估计值的一致性，使用多数规则，或使用概率的平均值（如果考虑概率主义模型）。因此

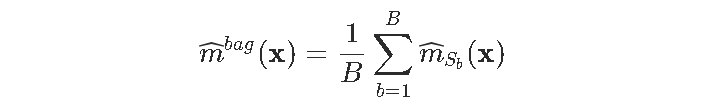
Bagging逻辑回归

考虑一下逻辑回归的情况。为了产生一个bootstrap样本，自然要使用上面描述的技术。即随机抽取一对(yi,xi)，均匀地（概率为）替换。这里考虑一下小数据集。对于bagging部分，使用以下代码

for(s in 1:1000){
df_s = df[sample(1:n,size=n,replace=TRUE)
logit[s]= glm(y~., df_s, family=binomial

然后，我们应该在这1000个模型上进行汇总，获得bagging的部分。

unlist(lapply(1:1000,function(z) predict(logit[z],nnd))}

我们现在对任何新的观察都有一个预测

vv = outer(vu,vu,(function(x,y) mean(pre(c(x,y)))
contour(vu,vu,vv,levels = .5,add=TRUE)

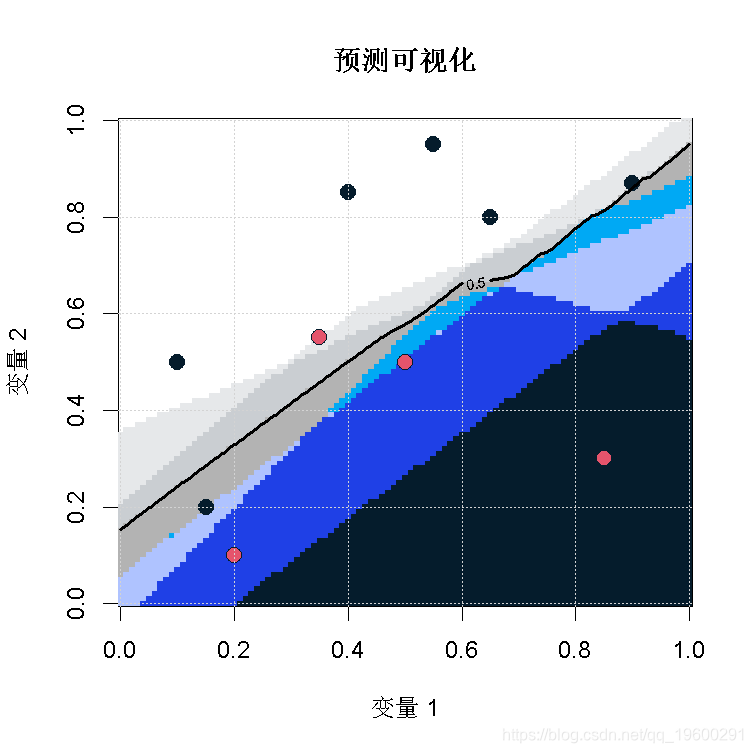
Bagging逻辑回归

另一种可用于生成bootstrap样本的技术是保留所有的xi，但对其中的每一个，都（随机地）抽取一个y的值，其中有

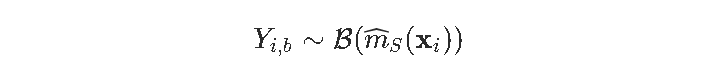
因此

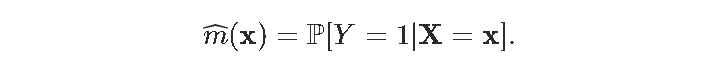
因此，现在Bagging算法的代码是

glm(y~x1+x2, df, family=binomial)
for(s in 1:100)
y = rbinom(size=1,prob=predict(reg,type="response")
L_logit[s] = glm(y~., df_s, family=binomial)

bagging算法的agg部分保持不变。在这里我们获得

vv = outer(vu,vu,(function(x,y) mean(pre(c(x,y)))))
contour(vu,vu,vv,levels = .5,add=TRUE)

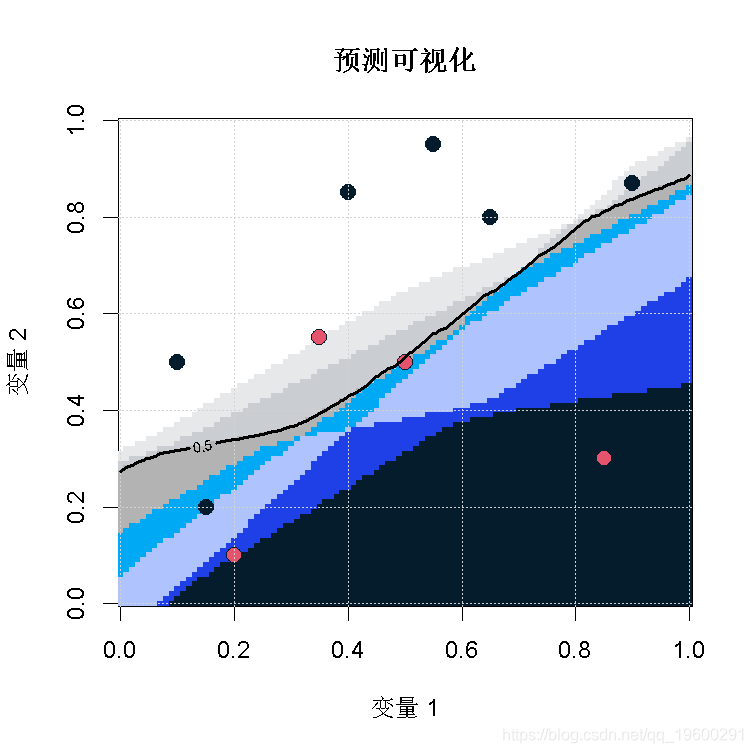
当然，我们可以使用该代码，检查预测获得我们的样本中的观察。

在这里考虑心肌梗塞数据。

数据

我们使用心脏病数据，预测急诊病人的心肌梗死，包含变量：

心脏指数
心搏量指数
舒张压
肺动脉压
心室压力
肺阻力
是否存活

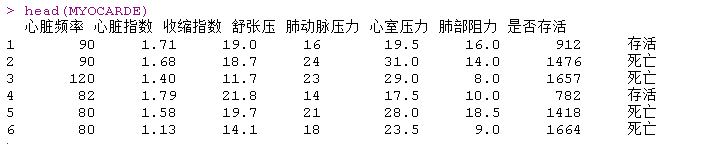
其中我们有急诊室的观察结果，对于心肌梗塞，我们想了解谁存活下来了，得到一个预测模型

reg = glm(as.factor(PRO)~., carde, family=binomial)
for(s in 1:1000){
L_logit[s] = glm(as.factor(PRO)~., my_s, family=binomial)
}
unlist(lapply(1:100,predict(L_logit[z],newdata=d,type="response")}

对于第一个观察，通过我们的1000个模拟数据集，以及我们的1000个模型，我们得到了以下死亡概率的估计。

v_x = p(x)
hist(v_x,proba=TRUE,breaks=seq(,by.05),=",="",
segments(mean(v_x),0,mean(v_x,5="=2)

因此，对于第一个观察，在78.8%的模型中，预测的概率高于50%，平均概率实际上接近75%。

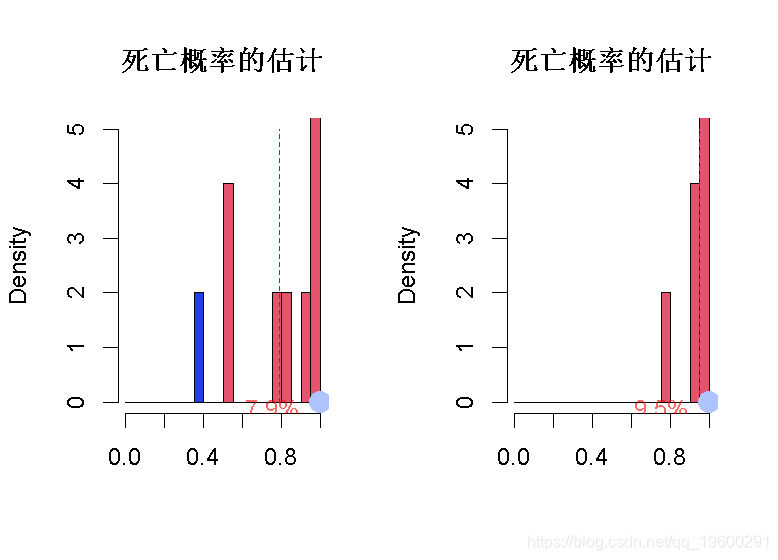
或者，对于样本22，预测与第一个非常接近。

histo(23)
histo(11)

我们在此观察到

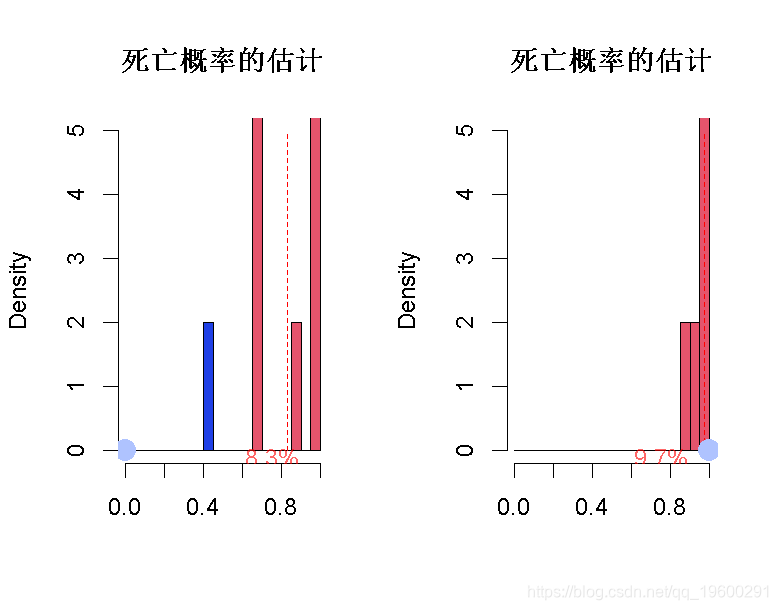
Bagging决策树

Bagging是由Leo Breiman于1994年在Bagging Predictors中介绍的。如果说第一节描述了这个程序，那么第二节则介绍了 "Bagging分类树"。树对于解释来说是不错的，但大多数时候，它们是相当差的预测模型。Bagging的想法是为了提高分类树的准确性。
bagging 的想法是为了生成大量的树

for(i in 1:12)
set.seed(sed[i])
idx = sample(1:n, size=n, replace=TRUE)
cart = rpart(PR~., md[idx,])

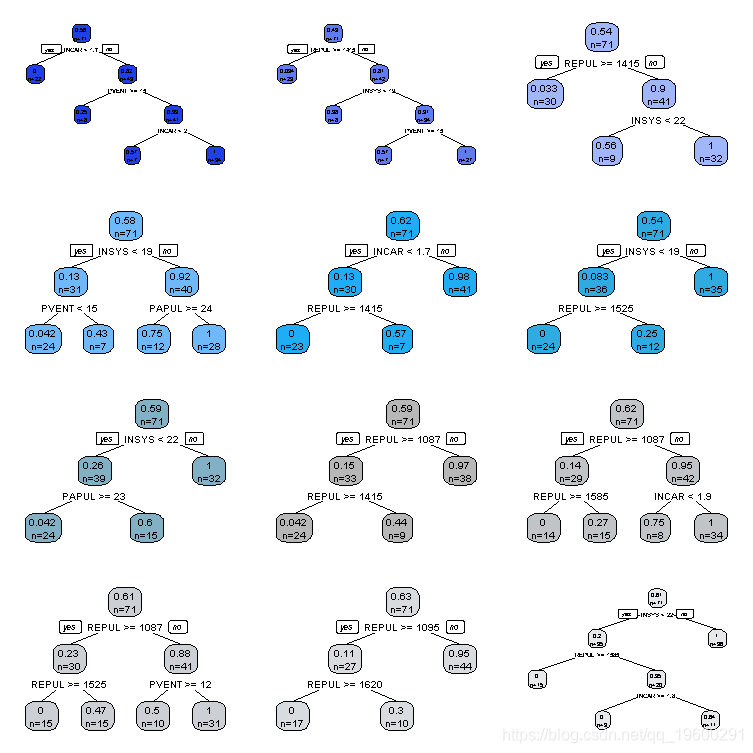
这个策略其实和以前一样。对于bootstrap部分，将树存储在一个列表中

for(s in 1:1000)
idx = sample(1:n, size=n, replace=TRUE)
L_tree[[s]] = rpart(as.(PR)~.)

而对于汇总部分，只需取预测概率的平均值即可

p = function(x){
unlist(lapply(1:1000,function(z) predict(L_tree[z],newdata,)[,2])

因为在这个例子中，我们无法实现预测的可视化，让我们在较小的数据集上运行同样的代码。

for(s in 1:1000){
idx = sample(1:n, size=n, replace=TRUE)
L_tree[s] = rpart(y~x1+x2,
}
unlist(lapply(1:1000,function(z) predict(L_tree[[z]])
outer(vu,vu,Vectorize(function(x,y) mean(p(c(x,y)))

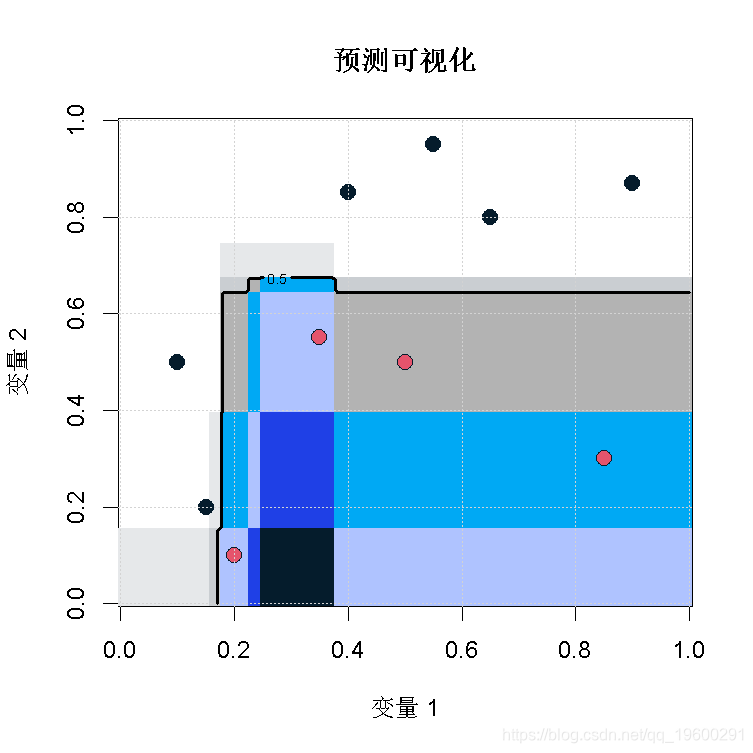
从bagging到森林

在这里，我们生成了很多树，但它并不是严格意义上的随机森林算法，正如1995年在《随机决策森林》中介绍的那样。实际上，区别在于决策树的创建。当我们有一个节点时，看一下可能的分割：我们考虑所有可能的变量，以及所有可能的阈值。这里的策略是在p中随机抽取k个变量（当然k<p，例如k=sqrt{p}）。这在高维度上是有趣的，因为在每次分割时，我们应该寻找所有的变量和所有的阈值，而这可能需要相当长的时间（尤其是在bootstrap 程序中，目标是长出1000棵树）。