拓端数据tecdat|R语言基于Bootstrap的线性回归预测置信区间估计方法

原文链接：http://tecdat.cn/?p=21625 

 

我们知道参数的置信区间的计算，这些都服从一定的分布(t分布、正态分布），因此在标准误前乘以相应的t分值或Z分值。但如果我们找不到合适的分布时，就无法计算置信区间了吗？幸运的是，有一种方法几乎可以用于计算各种参数的置信区间，这就是Bootstrap 法。

本文使用BOOTSTRAP来获得预测的置信区间。我们将在线性回归基础上讨论。

  1.  
     
  2.  
    > reg=lm(dist~speed,data=cars)
  3.  
    > points(x,predict(reg,newdata= data.frame(speed=x)))

 

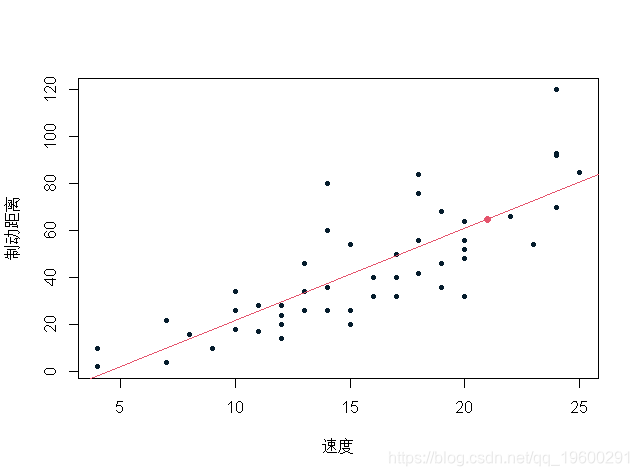
这是一个单点预测。当我们想给预测一个置信区间时，预测的置信区间取决于参数估计误差。

预测置信区间

让我们从预测的置信区间开始

  1.  
     
  2.  
    > for(s in 1:500){
  3.  
    + indice=sample(1:n,size=n,
  4.  
    + replace=TRUE)
  5.  
    + points(x,predict(reg,newdata=data.frame(speed=x)),pch=19,col="blue")
  6.  
     
  7.  
     

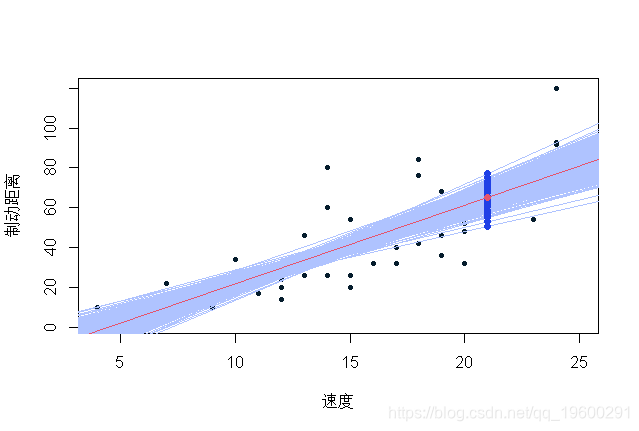
蓝色值是通过在我们的观测数据库中重新取样获得的可能预测值。值得注意的是，在残差正态性假设下（回归线的斜率和常数估计值），置信区间（90%）如下所示：

predict(reg,interval ="confidence",

 

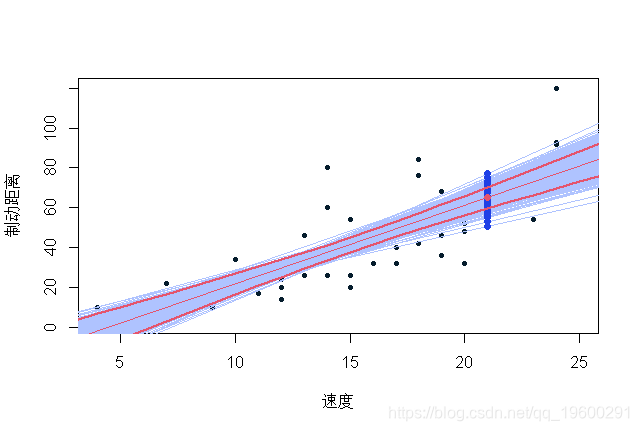
在这里，我们可以比较500个生成数据集上的值分布，并将经验分位数与正态假设下的分位数进行比较，

  1.  
    > hist(Yx,proba=TRUE
  2.  
    > boxplot(Yx,horizontal=TRUE
  3.  
    > polygon(c( x ,rev(x I]))))

 

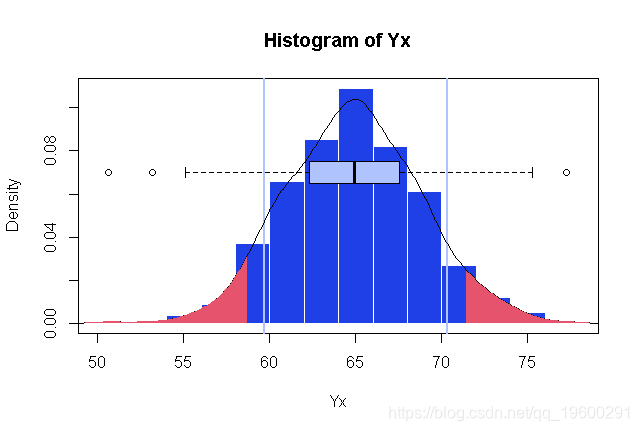
可以看出，经验分位数与正态假设下的分位数是可以比较的。

  1.  
    > quantile(Yx,c(.05,.95))
  2.  
    5% 95%
  3.  
    58.63689 70.31281
  4.  
    + level=.9,newdata=data.frame(speed=x))
  5.  
    fit lwr upr
  6.  
    1 65.00149 59.65934 70.34364

感兴趣变量的可能值

现在让我们看看另一种类型的置信区间，关于感兴趣变量的可能值。这一次，除了提取新样本和计算预测外，我们还将在每次绘制时添加噪声，以获得可能的值。

  1.  
    > for(s in 1:500){
  2.  
    + indice=sample(1:n,size=n,
  3.  
    + base=cars[indice,]
  4.  
    + erreur=residuals(reg)
  5.  
    + predict(reg,newdata=data.frame(speed=x))+E

 

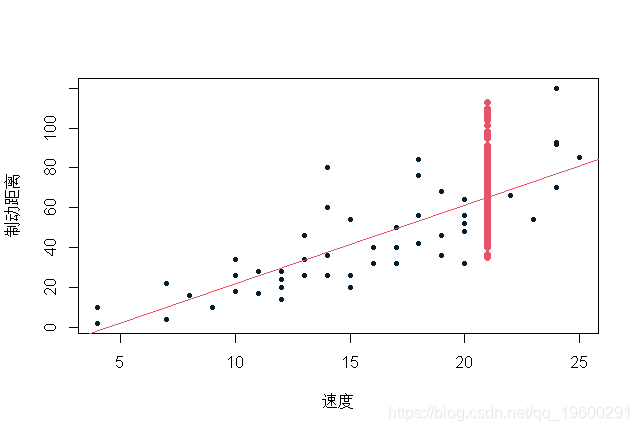
在这里，我们可以（首先以图形方式）比较通过重新取样获得的值和在正态假设下获得的值，

  1.  
    > hist(Yx,proba=TRUE)
  2.  
    > boxplot(Yx) abline(v=U[2:3)
  3.  
    > polygon(c(D$x[I,rev(D$x[I])

 

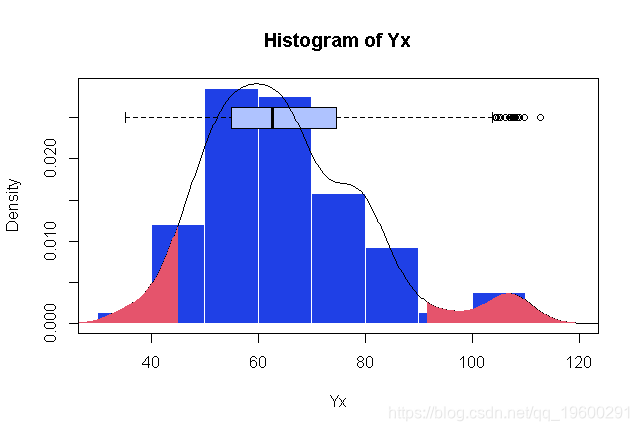
数值上给出了以下比较

  1.  
    > quantile(Yx,c(.05,.95))
  2.  
    5% 95%
  3.  
    44.43468 96.01357
  4.  
    U=predict(reg,interval ="prediction"
  5.  
    fit lwr upr
  6.  
    1 67.63136 45.16967 90.09305

这一次，右侧有轻微的不对称。显然，我们不能假设高斯残差，因为有更大的正值，而不是负值。考虑到数据的性质，这是有意义的（制动距离不能是负数）。

然后开始讨论在供应中使用回归模型。为了获得具有独立性，有人认为必须使用增量付款的数据，而不是累计付款。

可以创建一个数据库，解释变量是行和列。

  1.  
    > base=data.frame(
  2.  
    + y
  3.  
     
  4.  
    > head(base,12)
  5.  
    y ai bj
  6.  
    1 3209 2000 0
  7.  
    2 3367 2001 0
  8.  
    3 3871 2002 0
  9.  
    4 4239 2003 0
  10.  
    5 4929 2004 0
  11.  
    6 5217 2005 0
  12.  
    7 1163 2000 1
  13.  
    8 1292 2001 1
  14.  
    9 1474 2002 1
  15.  
    10 1678 2003 1
  16.  
    11 1865 2004 1
  17.  
    12 NA 2005 1

然后，我们可以从基于对数增量付款数据的回归模型开始，该模型基于对数正态模型

  1.  
     
  2.  
     
  3.  
    Coefficients:
  4.  
    Estimate Std. Error t value Pr(>|t|)
  5.  
    (Intercept) 7.9471 0.1101 72.188 6.35e-15 ***
  6.  
    as.factor(ai)2001 0.1604 0.1109 1.447 0.17849
  7.  
    as.factor(ai)2002 0.2718 0.1208 2.250 0.04819 *
  8.  
    as.factor(ai)2003 0.5904 0.1342 4.399 0.00134 **
  9.  
    as.factor(ai)2004 0.5535 0.1562 3.543 0.00533 **
  10.  
    as.factor(ai)2005 0.6126 0.2070 2.959 0.01431 *
  11.  
    as.factor(bj)1 -0.9674 0.1109 -8.726 5.46e-06 ***
  12.  
    as.factor(bj)2 -4.2329 0.1208 -35.038 8.50e-12 ***
  13.  
    as.factor(bj)3 -5.0571 0.1342 -37.684 4.13e-12 ***
  14.  
    as.factor(bj)4 -5.9031 0.1562 -37.783 4.02e-12 ***
  15.  
    as.factor(bj)5 -4.9026 0.2070 -23.685 4.08e-10 ***
  16.  
    ---
  17.  
    Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
  18.  
     
  19.  
    Residual standard error: 0.1753 on 10 degrees of freedom
  20.  
    (15 observations deleted due to missingness)
  21.  
    Multiple R-squared: 0.9975, Adjusted R-squared: 0.9949
  22.  
    F-statistic: 391.7 on 10 and 10 DF, p-value: 1.338e-11
  23.  
     
  24.  
    >
  25.  
    exp(predict(reg1,
  26.  
    + newdata=base)+summary(reg1)$sigma^2/2)
  27.  
     
  28.  
    [,1] [,2] [,3] [,4] [,5] [,6]
  29.  
    [1,] 2871.2 1091.3 41.7 18.3 7.8 21.3
  30.  
    [2,] 3370.8 1281.2 48.9 21.5 9.2 25.0
  31.  
    [3,] 3768.0 1432.1 54.7 24.0 10.3 28.0
  32.  
    [4,] 5181.5 1969.4 75.2 33.0 14.2 38.5
  33.  
    [5,] 4994.1 1898.1 72.5 31.8 13.6 37.1
  34.  
    [6,] 5297.8 2013.6 76.9 33.7 14.5 39.3
  35.  
     
  36.  
    > sum(py[is.na(y)])
  37.  
    [1] 2481.857

这与链式梯度法的结果略有不同，但仍然具有可比性。我们也可以尝试泊松回归（用对数链接）

  1.  
    glm(y~
  2.  
    + as.factor(ai)+
  3.  
    + as.factor(bj),data=base,
  4.  
    + family=poisson)
  5.  
     
  6.  
     
  7.  
    Coefficients:
  8.  
    Estimate Std. Error z value Pr(>|z|)
  9.  
    (Intercept) 8.05697 0.01551 519.426 < 2e-16 ***
  10.  
    as.factor(ai)2001 0.06440 0.02090 3.081 0.00206 **
  11.  
    as.factor(ai)2002 0.20242 0.02025 9.995 < 2e-16 ***
  12.  
    as.factor(ai)2003 0.31175 0.01980 15.744 < 2e-16 ***
  13.  
    as.factor(ai)2004 0.44407 0.01933 22.971 < 2e-16 ***
  14.  
    as.factor(ai)2005 0.50271 0.02079 24.179 < 2e-16 ***
  15.  
    as.factor(bj)1 -0.96513 0.01359 -70.994 < 2e-16 ***
  16.  
    as.factor(bj)2 -4.14853 0.06613 -62.729 < 2e-16 ***
  17.  
    as.factor(bj)3 -5.10499 0.12632 -40.413 < 2e-16 ***
  18.  
    as.factor(bj)4 -5.94962 0.24279 -24.505 < 2e-16 ***
  19.  
    as.factor(bj)5 -5.01244 0.21877 -22.912 < 2e-16 ***
  20.  
    ---
  21.  
    Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
  22.  
     
  23.  
    (Dispersion parameter for poisson family taken to be 1)
  24.  
     
  25.  
    Null deviance: 46695.269 on 20 degrees of freedom
  26.  
    Residual deviance: 30.214 on 10 degrees of freedom
  27.  
    (15 observations deleted due to missingness)
  28.  
    AIC: 209.52
  29.  
     
  30.  
    Number of Fisher Scoring iterations: 4
  31.  
     
  32.  
    > predict(reg2,
  33.  
    newdata=base,type="response")
  34.  
     
  35.  
    > sum(py2[is.na(y)])
  36.  
    [1] 2426.985

预测结果与链式梯度法得到的估计值吻合。克劳斯·施密特（Klaus Schmidt）和安吉拉·温什（Angela Wünsche）于1998年在链式梯度法、边际和最大似然估计中建立了与最小偏差方法的联系。

最受欢迎的见解

1.R语言多元Logistic逻辑回归 应用案例

2.面板平滑转移回归(PSTR)分析案例实现

3.matlab中的偏最小二乘回归（PLSR）和主成分回归（PCR）

4.R语言泊松Poisson回归模型分析案例

5.R语言回归中的Hosmer-Lemeshow拟合优度检验

6.r语言中对LASSO回归，Ridge岭回归和Elastic Net模型实现

7.在R语言中实现Logistic逻辑回归

8.python用线性回归预测股票价格

9.R语言如何在生存分析与Cox回归中计算IDI，NRI指标

posted @ 2021-05-12 00:39  拓端tecdat  阅读(943)  评论(0)  编辑  收藏  举报