拓端数据tecdat|R语言自适应LASSO 多项式回归、二元逻辑回归和岭回归应用分析
原文链接:http://tecdat.cn/?p=21602
正则化(regularization)
正则化路径是在正则化参数lambda的值网格上计算套索LASSO或弹性网路惩罚的正则化路径。该算法速度快,可以利用输入矩阵x中的稀疏性,拟合线性、logistic和多项式、poisson和Cox回归模型。可以通过拟合模型进行各种预测。它还可以拟合多元线性回归。”
例子
加载数据
这里加载了一个高斯(连续Y)的例子。
as_data_frame(y)-
## # A tibble: 100 x 1
-
## V1
-
## <dbl>
-
## 1 -1.2748860
-
## 2 1.8434251
-
## 3 0.4592363
-
## 4 0.5640407
-
## 5 1.8729633
-
## 6 0.5275317
-
## 7 2.4346589
-
## 8 -0.8945961
-
## 9 -0.2059384
-
## 10 3.1101188
-
## # ... with 90 more rows
初始岭回归
cv.glmnet执行k-折交叉验证 .
-
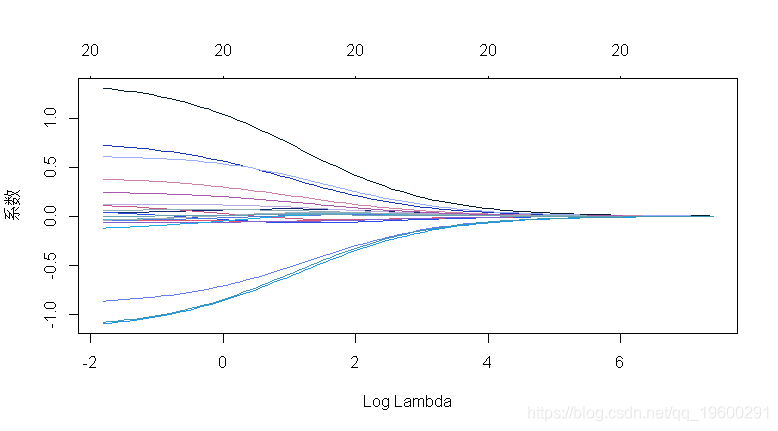
## 执行岭回归
-
glmnet(x , y
-
## “alpha=1”是套索惩罚, “alpha=0”是岭惩罚。
-
alpha = 0)
-
## 用10折CV进行岭回归
-
cv.glmnet(
-
## 类型.测量:用于交叉验证的丢失。
-
type.measure = "mse",
-
## K = 10 是默认值。
-
nfold = 10,
-
##“alpha=1”是套索惩罚,“alpha=0”是岭惩罚。
-
alpha = 0)
-
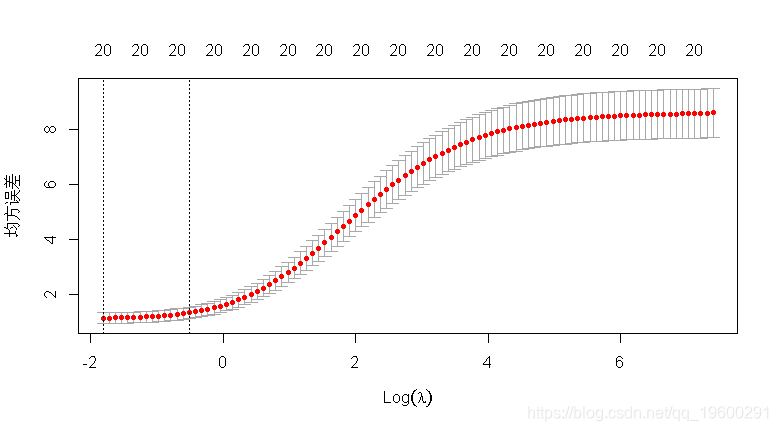
## 惩罚vs CV MSE图
-
## 在误差最小λ处提取系数
-
cv$lambda.min
## [1] 0.1789759-
## s:需要进行预测的惩罚参数“lambda”的值。默认值是用于创建模型的整个序列。
-
coef( s = lambda.min)
-
## 21 x 1 sparse Matrix of class "dgCMatrix"
-
## 1
-
## (Intercept) 0.149041059
-
## V1 1.302684272
-
## V2 0.035835380
-
## V3 0.719936146
-
## V4 0.036473087
-
## V5 -0.863490158
-
## V6 0.605750873
-
## V7 0.123446432
-
## V8 0.376890626
-
## V9 -0.040012847
-
## V10 0.105999328
-
## V11 0.240967604
-
## V12 -0.066363634
-
## V13 -0.042048935
-
## V14 -1.092107794
-
## V15 -0.119566353
-
## V16 -0.035859663
-
## V17 -0.038827463
-
## V18 0.061785988
-
## V19 -0.001409608
-
## V20 -1.079879797
-
## 截距估计应该剔除。
-
(coef(cv, s = lambda.min))[-1]
这个初始过程给出了基于10折交叉验证选择的最佳岭回归模型的一组系数,使用平方误差度量![]() 作为模型性能度量。
作为模型性能度量。
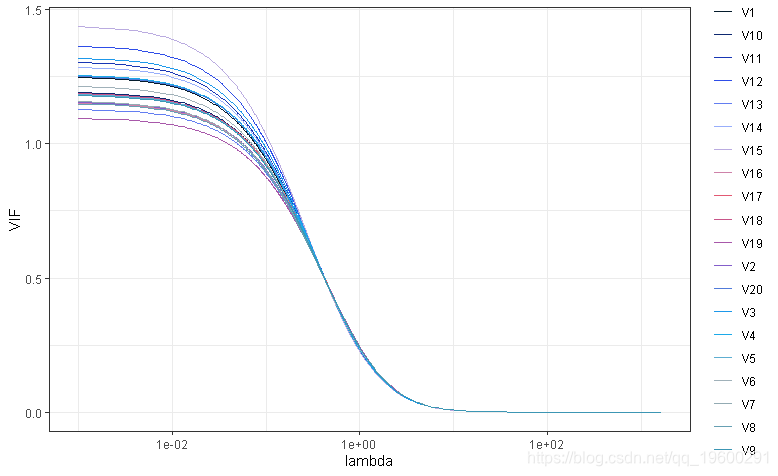
KNNL和Hadi中提到的另一种选择lambda的方法是选择最小的lambda,这样系数的轨迹是稳定的,VIF变得足够小。在这种情况下,VIF的定义必须包括惩罚因子lambda,这在Hadi的p295和knll的p436中有说明。
![]()
![]() 是标准化的协变量矩阵.
是标准化的协变量矩阵. ![]() 是原始非标准化协变量的相关矩阵
是原始非标准化协变量的相关矩阵 ![]() . 该计算可定义如下。
. 该计算可定义如下。
-
vif <- function(x, lambda) {
-
ZtZ <- cor(x)
-
diag(solve(ZtZ + lambdaI %*% ZtZ %*% solve(ZtZ + lambdaI)
-
-
##
-
-
ggplot(mapping = aes(x = lambda, y = value, group = key, color = key)) +
-
geom_line() +
-
-
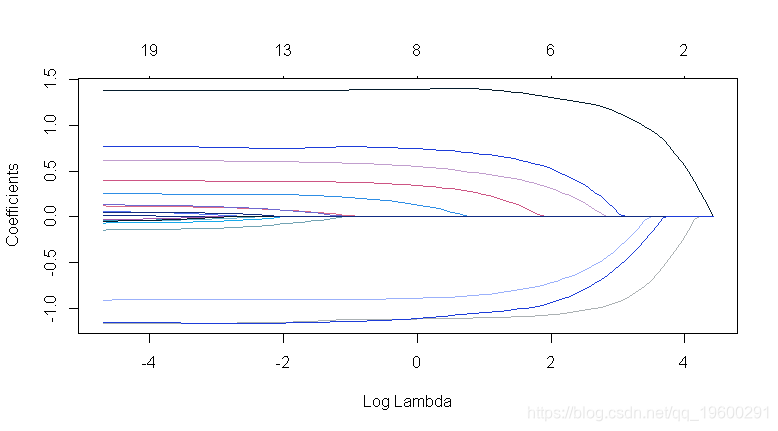
自适应LASSO
-
## 执行自适应LASSO
-
glmnet(x = y =
-
## 类型。度量:用于交叉验证的损失。
-
##“alpha=1”是套索惩罚,“alpha=0”是岭惩罚。
-
alpha = 1,
-
##
-
## 惩罚系数:可以对每个系数应用单独的惩罚因子。这是一个乘以“lambda”以允许差异收缩的数字。对于某些变量可以是0, 这意味着没有收缩,而且这个变量总是包含在模型中。对于所有变量,默认值为1(对于“exclude”中列出的变量,默认值为无限大)。注意:惩罚因子在内部被重新调整为与nvars相加,lambda序列将反映这种变化。
-
## 使用10折CV执行自适应套索
-
-
## 类型。度量:用于交叉验证的损失。
-
类型。测量= " mse ",
-
## K = 10 是默认值。
-
nfold = 10,
-
## ‘alpha = 1’ 是套索惩罚,'alpha=0'是岭惩罚。
-
##
-
## 惩罚系数:可以对每个系数应用单独的惩罚因子。这是一个乘以“lambda”以允许差异收缩的数字。对于某些变量可以为0,这意味着没有收缩,并且该变量始终包含在模型中。对于所有变量,默认值为1(对于“exclude”中列出的变量,默认值为无限大)。注意:惩罚因子在内部被重新调整为与nvars相加,lambda序列将反映这种变化。
-
## 惩罚vs CV MSE图
-
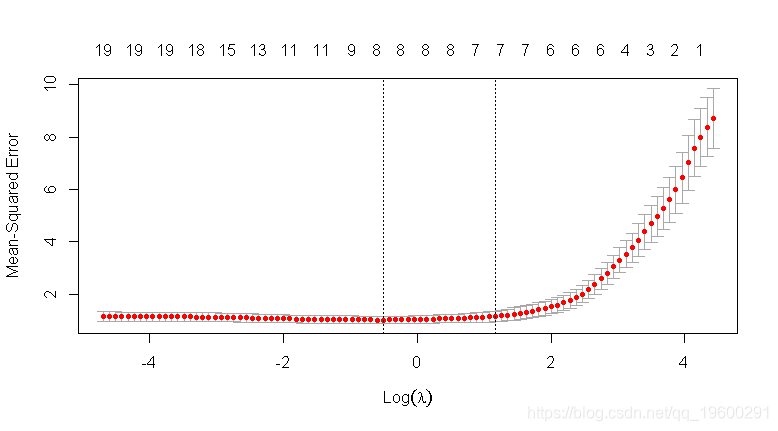
-
## 在误差最小λ处提取系数
-
lambda.min
## [1] 0.7193664-
## s:需要进行预测的惩罚参数“lambda”的值。默认值是用于创建模型的整个序列。
-
best_alasso_coef1
-
## 21 x 1 sparse Matrix of class "dgCMatrix"
-
## 1
-
## (Intercept) 0.1269539
-
## V1 1.3863728
-
## V2 .
-
## V3 0.7573538
-
## V4 .
-
## V5 -0.8937983
-
## V6 0.5718800
-
## V7 .
-
## V8 0.3654255
-
## V9 .
-
## V10 .
-
## V11 0.1824140
-
## V12 .
-
## V13 .
-
## V14 -1.1150736
-
## V15 .
-
## V16 .
-
## V17 .
-
## V18 .
-
## V19 .
-
## V20 -1.1268794
那个惩罚系数参数允许指定系数特定的惩罚级别。这里我们使用自适应LASSO惩罚,即最佳岭系数绝对值的逆。
最终模型Rsquare
-
## R^2函数
-
## https://en.wikipedia.org/wiki/Coefficient_of_determination
-
## 总SS
-
ss_tot <- sum((y - ybar)^2)
-
## 剩余 SS
-
ss_res <- sum((y - yhat)^2)
-
## R^2 = 1 - ss_res/ ss_tot
-
-
## 调整R^2函数
-
## n个样本,p个参数
-
-
## 获取 R^2
-
r_sq(as.vector(y_cont), as.vector(predict(alasso1, newx =
## [1] 0.906806-
##获得调整R ^ 2
-
adj_r_sq(r_squared_alasso1, n = nrow(y_cont),
## [1] 0.9007934-
## 交叉验证测试集R^2
-
## alasso1_cv$cvm[1] 是截距模型的交叉验证测试集均方误差。
-
1 - cvm[lambda == lambda.min] / cvm[1]
## [1] 0.8854662交叉验证测试集Rsquare
-
lapply(unique( foldid), function(id) {
-
## 拟合排除测试集 (foldid == id)
-
glmnet(x = x_cont[alasso1_cv$foldid != id,],
-
y = y_cont[alasso1_cv$foldid != id],
-
## 使用模型拟合最佳lambda测试集Yïhat
-
predict(fit, newx = x_cont[alasso1_cv$foldid == id,],
-
## 测试组 R^2
-
1 - sum((y - y_pred)^2) / sum((y - mean(y))^2)
-
}) %>%
-
## [1] 0.8197796 0.9090972 0.9499495 0.8019303 0.8637534 0.7184797 0.8579943 0.9250376 0.8300891
-
## [10] 0.9188004
## [1] 0.8594911多项式例子
-
## # A tibble: 500 x 30
-
## V1 V2 V3 V4 V5 V6 V7 V8
-
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
-
## 1 0.8212500 1.2155090 -0.64860899 -0.7001262 -1.9640742 1.1692107 0.28598652 -0.1664266
-
## 2 0.9264925 -1.1855031 -1.18297879 0.9828354 1.0693610 -0.2302219 0.57772625 -0.8738714
-
## 3 -1.5719712 0.8568961 -0.02208733 1.7445962 -0.4148403 -2.0289054 -1.31228181 -1.2441528
-
## 4 0.7419447 -0.9452052 -1.61821790 1.0015587 -0.4589488 0.5154490 0.29189973 0.1114092
-
## 5 -0.1333660 0.5085678 0.04739909 -0.4486953 -0.2616950 -0.1554108 -1.24834832 -1.0498054
-
## 6 -0.5672062 0.6020396 -2.10300909 0.3119233 0.3272173 -0.8671885 0.97512759 -0.7216256
-
## 7 1.9683411 2.5162198 1.61109738 1.0047913 -0.5194647 1.0738680 -0.16176095 -0.4267418
-
## 8 0.2857727 -1.7017703 1.41062569 -0.5823727 -1.3330908 1.7929250 0.06396841 -0.6818909
-
## 9 -0.5339434 0.1725089 0.93504676 -1.9956942 -0.9021089 -0.2624043 0.97406411 0.5166823
-
## 10 0.8081052 -0.9662501 0.54666915 -0.8388913 0.9665053 1.4039598 0.63502500 0.3429640
-
## # ... with 490 more rows, and 22 more variables: V9 <dbl>, V10 <dbl>, V11 <dbl>, V12 <dbl>,
-
## # V13 <dbl>, V14 <dbl>, V15 <dbl>, V16 <dbl>, V17 <dbl>, V18 <dbl>, V19 <dbl>, V20 <dbl>,
-
## # V21 <dbl>, V22 <dbl>, V23 <dbl>, V24 <dbl>, V25 <dbl>, V26 <dbl>, V27 <dbl>, V28 <dbl>,
-
## # V29 <dbl>, V30 <dbl>
as_data_frame(y)-
## # A tibble: 500 x 1
-
## value
-
## <dbl>
-
## 1 3
-
## 2 2
-
## 3 2
-
## 4 2
-
## 5 3
-
## 6 3
-
## 7 3
-
## 8 1
-
## 9 1
-
## 10 1
-
## # ... with 490 more rows
-
-
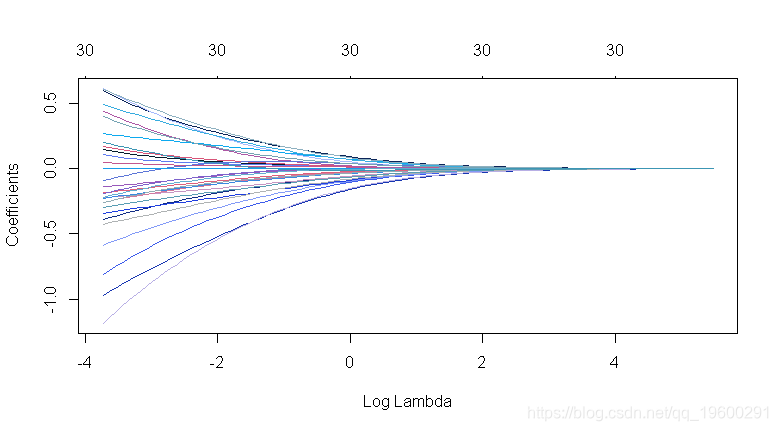
plot(ridge2, xvar = "lambda")
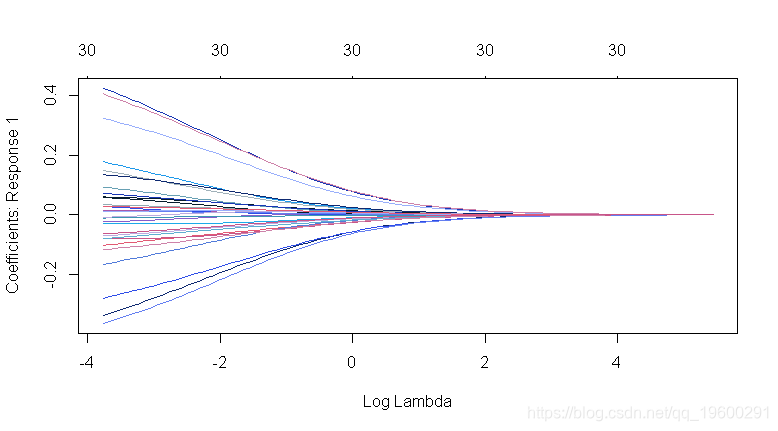
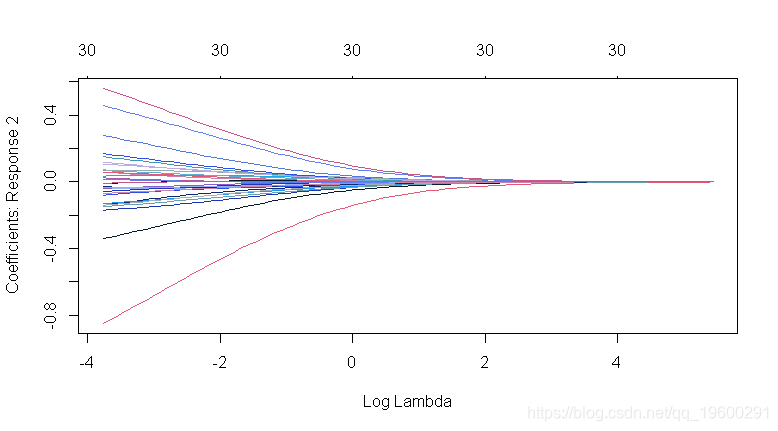
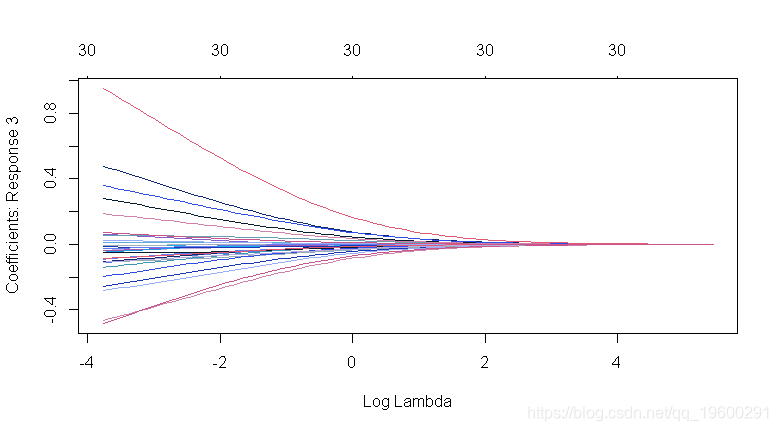
-
## 用10折交叉验证CV进行岭回归
-
## 类型.测量:用于交叉验证的损失。
-
类型.测量=“偏差”,
-
-
## 多项式回归
-
## ‘alpha = 1’ 是套索惩罚,'alpha=0'是岭惩罚。
-
## 惩罚vs CV MSE图
-
plot(ridge2_cv)
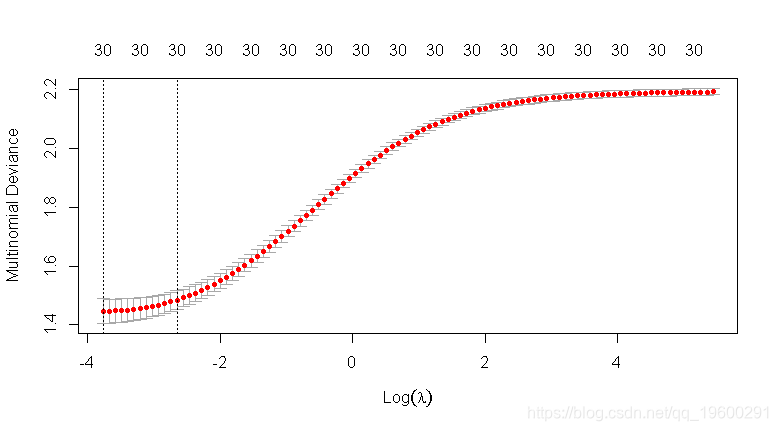
-
## 在误差最小λ处提取系数
-
lambda.min
## [1] 0.02540802-
## s:需要进行预测的惩罚参数“lambda”的值。默认值是用于创建模型的整个序列。
-
do.call(cbind, coef( cv, s = lambda.min))
-
## 31 x 3 sparse Matrix of class "dgCMatrix"
-
## 1 1 1
-
## (Intercept) -0.030926870 -0.012579891 0.043506761
-
## V1 0.056754184 -0.332936704 0.276182520
-
## V2 -0.330771038 -0.135465951 0.466236989
-
## V3 0.417313228 -0.166953973 -0.250359256
-
## V4 -0.275107590 -0.075937714 0.351045304
-
## V5 -0.359310997 0.447318724 -0.088007727
-
## V6 0.318490592 -0.042273343 -0.276217249
-
## V7 -0.069203544 0.103874053 -0.034670509
-
## V8 0.398432356 0.056457793 -0.454890149
-
## V9 -0.100873703 -0.831473315 0.932347018
-
## V10 -0.079409535 0.550465763 -0.471056227
-
## V11 0.015539259 0.022872091 -0.038411350
-
## V12 -0.023384035 -0.037367749 0.060751784
-
## V13 -0.162456798 0.271096200 -0.108639401
-
## V14 0.173128811 -0.127758267 -0.045370544
-
## V15 -0.029448593 0.035626357 -0.006177764
-
## V16 -0.078135662 0.066353666 0.011781996
-
## V17 0.144753874 -0.137960413 -0.006793461
-
## V18 0.032929352 0.071275386 -0.104204738
-
## V19 0.090783173 -0.147044947 0.056261774
-
## V20 -0.010749594 0.146821172 -0.136071578
-
## V21 0.059468598 -0.008259112 -0.051209485
-
## V22 0.133514075 -0.030352819 -0.103161256
-
## V23 0.070174614 -0.054781769 -0.015392844
-
## V24 0.027344225 0.164797661 -0.192141886
-
## V25 0.010677968 0.014023080 -0.024701049
-
## V26 0.010490474 -0.034644559 0.024154085
-
## V27 -0.008201249 0.114562955 -0.106361705
-
## V28 -0.115249536 -0.067581191 0.182830727
-
## V29 0.027760120 0.056857406 -0.084617526
-
## V30 -0.062642211 -0.007339614 0.069981825
-
## 转换为矩阵
-
## 截距估计应该取消。
-
1 / abs(as.matrix(best_ridge_coef2)[-1,])
-
## 1 1 1
-
## V1 17.619846 3.003574 3.620794
-
## V2 3.023239 7.381929 2.144832
-
## V3 2.396282 5.989675 3.994260
-
## V4 3.634942 13.168687 2.848635
-
## V5 2.783104 2.235542 11.362639
-
## V6 3.139810 23.655569 3.620339
-
## V7 14.450127 9.627043 28.842957
-
## V8 2.509836 17.712347 2.198333
-
## V9 9.913386 1.202684 1.072562
-
## V10 12.592946 1.816643 2.122889
-
## V11 64.353133 43.721407 26.033972
-
## V12 42.764219 26.761045 16.460422
-
## V13 6.155483 3.688727 9.204764
-
## V14 5.776046 7.827282 22.040732
-
## V15 33.957479 28.069106 161.870875
-
## V16 12.798253 15.070757 84.875262
-
## V17 6.908278 7.248456 147.200381
-
## V18 30.368044 14.030089 9.596493
-
## V19 11.015257 6.800642 17.774057
-
## V20 93.026766 6.811007 7.349073
-
## V21 16.815597 121.078385 19.527632
-
## V22 7.489847 32.945869 9.693562
-
## V23 14.250167 18.254248 64.965251
-
## V24 36.570794 6.068047 5.204487
-
## V25 93.650773 71.311008 40.484111
-
## V26 95.324582 28.864561 41.400864
-
## V27 121.932644 8.728825 9.401880
-
## V28 8.676825 14.797016 5.469540
-
## V29 36.022899 17.587858 11.817883
-
## V30 15.963677 136.246945 14.289424
-
## 执行自适应套索
-
## 多项式回归
-
family = "multinomial",
-
## ‘alpha = 1’ 是套索惩罚,'alpha=0'是岭惩罚。
-
alpha = 1,
-
##
-
## 惩罚系数:可以对每个系数应用单独的惩罚因子。这是一个乘以“lambda”以允许差异收缩的数字。对于某些变量可以为0,这意味着没有收缩,并且该变量始终包含在模型中。对于所有变量,默认值为1(对于“exclude”中列出的变量,默认值为无限大)。注意:惩罚因子在内部被重新调整为与nvars相加,lambda序列将反映这种变化。
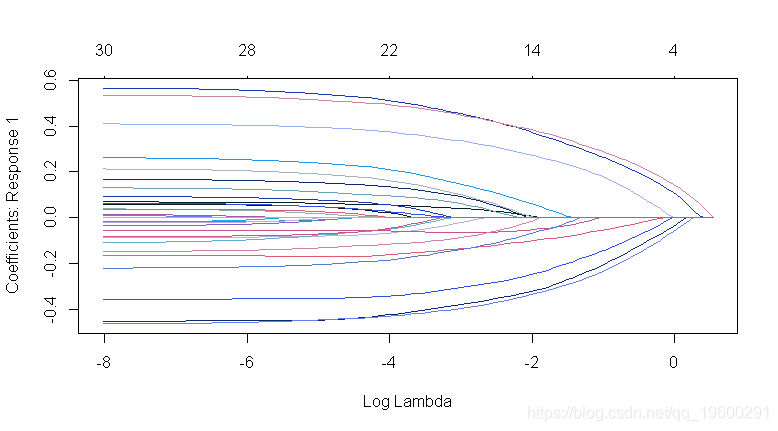
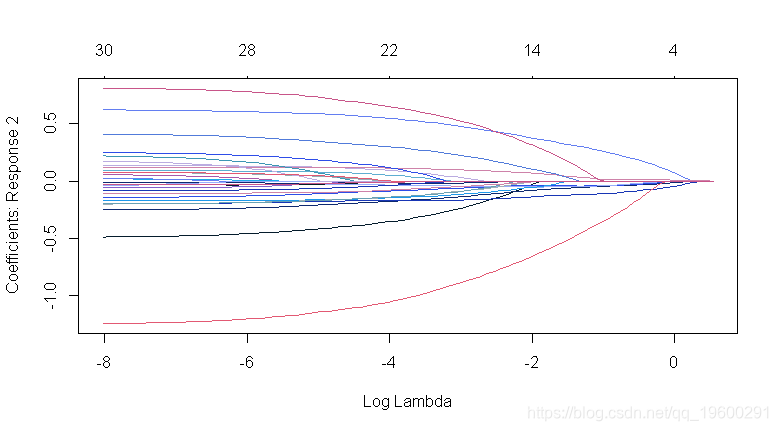
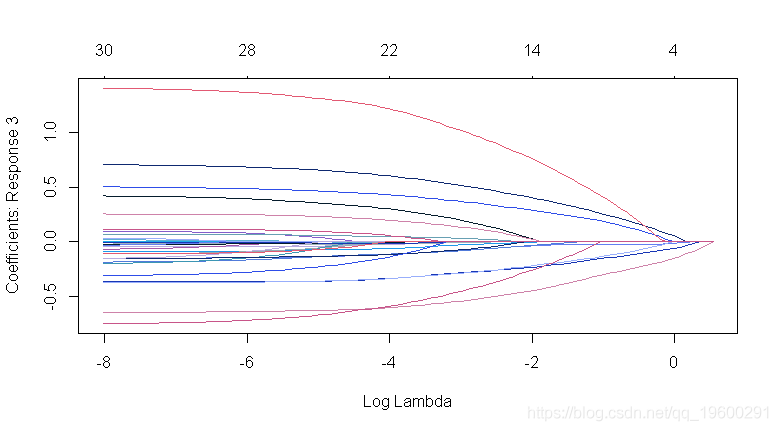
-
## 使用10折CV执行自适应套索
-
## 类型。度量:用于交叉验证的损失。
-
type.measure = "偏差",
-
-
## 惩罚vs CV MSE图
-
plot(alasso2_cv)
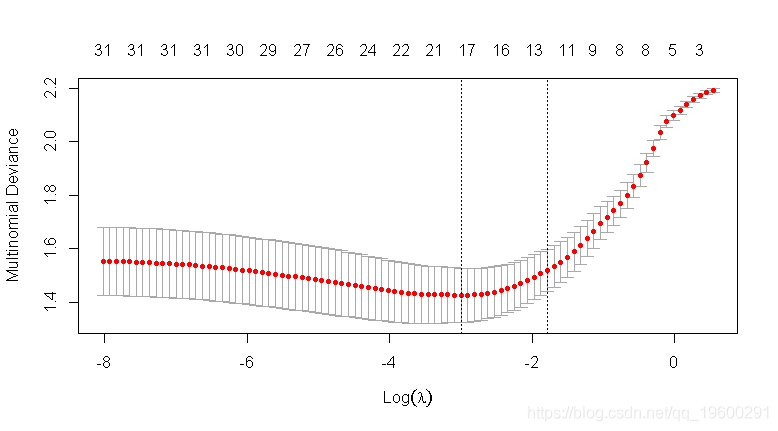
-
## 在误差最小λ处提取系数
-
lambda.min
## [1] 0.023834-
## s:需要进行预测的惩罚参数“lambda”的值。默认值是用于创建模型的整个序列。
-
do.call(cbind, coef(alasso2_cv, s = lambda.min))
-
## 31 x 3 sparse Matrix of class "dgCMatrix"
-
## 1 1 1
-
## (Intercept) 0.001070916 0.029687114 -0.030758030
-
## V1 0.051853991 -0.329785101 0.277931110
-
## V2 -0.414609162 -0.166765504 0.581374666
-
## V3 0.498638681 -0.172468859 -0.326169822
-
## V4 -0.336005338 -0.079578260 0.415583598
-
## V5 -0.424216967 0.532071434 -0.107854467
-
## V6 0.364828074 -0.035326316 -0.329501758
-
## V7 -0.058746523 0.080343071 -0.021596548
-
## V8 0.483592031 0.111422669 -0.595014699
-
## V9 -0.155745580 -1.016502806 1.172248386
-
## V10 -0.060698812 0.625050169 -0.564351357
-
## V11 . . .
-
## V12 . . .
-
## V13 -0.175719655 0.283930678 -0.108211023
-
## V14 0.196421536 -0.139576235 -0.056845300
-
## V15 . . .
-
## V16 -0.037414770 0.040300172 -0.002885402
-
## V17 0.149438019 -0.129742710 -0.019695308
-
## V18 . . .
-
## V19 0.088822086 -0.130605368 0.041783282
-
## V20 . . .
-
## V21 0.007141749 -0.002869644 -0.004272105
-
## V22 0.125997952 -0.016924514 -0.109073438
-
## V23 0.043024971 -0.026879150 -0.016145821
-
## V24 0.016862193 0.083686360 -0.100548554
-
## V25 . . .
-
## V26 . . .
-
## V27 . . .
-
## V28 -0.111429811 -0.069842376 0.181272187
-
## V29 . . .
-
## V30 -0.032032333 -0.006590025 0.038622358
最终模型正确分类率
xtabs(~ y_multi_pred_class + y_multi)-
## y_multi
-
## y_multi_pred_class 1 2 3
-
## 1 84 20 16
-
## 2 30 136 19
-
## 3 28 18 149
mean(y_multi == y_multi_pred_class)## [1] 0.738交叉验证测试集正确分类率
-
lapply(unique(foldid), function(id) {
-
## 拟合排除测试集(foldid==id)
-
-
## 使用模型拟合最佳lambda测试集Yïhat
-
y_pred <- (predict(fit, newx = x_multi[foldid == id,], type = "class",
-
s = lambda.min))
-
## 测试集Y
-
y <- y_multi[foldid == id]
-
## 测试集CCR
-
mean(y == y_pred)
-
}) %>%
## [1] 0.68 0.64 0.76 0.72 0.70 0.66 0.60 0.72 0.62 0.76## [1] 0.686二元逻辑回归示例
-
## # A tibble: 100 x 30
-
## V1 V2 V3 V4 V5 V6 V7 V8
-
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
-
## 1 -0.61926135 0.01624409 -0.62606831 0.41268461 0.4944374 -0.4493269 0.6760053 -0.06771419
-
## 2 1.09427278 0.47257285 -1.33714704 -0.64058126 0.2823199 -0.6093321 0.3547232 -0.62686515
-
## 3 -0.35670402 0.30121334 0.19056192 0.23402677 0.1698086 1.2291427 1.1628095 0.88024242
-
## 4 -2.46907012 2.84771447 1.66024352 1.56881297 -0.8330570 -0.5620088 -0.6142455 -1.76529838
-
## 5 0.56728852 0.88888747 -0.01158671 0.57627526 -0.8689453 -0.3132571 0.6902907 -1.29961200
-
## 6 0.91292543 0.77350086 0.55836355 -0.53509922 0.3507093 -0.5763021 -0.3882672 0.55518663
-
## 7 0.09567305 0.14027229 -0.76043921 -0.04935541 1.5740992 -0.1240903 -1.1106276 1.72895452
-
## 8 1.93420667 -0.71114983 -0.27387147 1.00113828 1.0439012 0.8028893 -0.6035769 -0.51136380
-
## 9 0.28275701 1.05940570 -0.03944966 0.30277367 -0.9161762 0.6914934 0.6087553 0.30921594
-
## 10 0.80143492 1.53674274 -1.01230763 -0.38480878 -2.0319100 0.2236314 -1.1628847 -0.52739792
-
## # ... with 90 more rows, and 22 more variables: V9 <dbl>, V10 <dbl>, V11 <dbl>, V12 <dbl>,
-
## # V13 <dbl>, V14 <dbl>, V15 <dbl>, V16 <dbl>, V17 <dbl>, V18 <dbl>, V19 <dbl>, V20 <dbl>,
-
## # V21 <dbl>, V22 <dbl>, V23 <dbl>, V24 <dbl>, V25 <dbl>, V26 <dbl>, V27 <dbl>, V28 <dbl>,
-
## # V29 <dbl>, V30 <dbl>
as_data_frame(y)-
## # A tibble: 100 x 1
-
## value
-
## <int>
-
## 1 0
-
## 2 1
-
## 3 1
-
## 4 0
-
## 5 1
-
## 6 0
-
## 7 0
-
## 8 0
-
## 9 1
-
## 10 1
-
## # ... with 90 more rows
-
-
## 执行岭回归
-
## 二元逻辑回归
-
family = "binomial",
-
## “alpha=1”是套索惩罚,“alpha=0”是岭惩罚。
-
##用10折CV进行岭回归
-
##类型。度量:用于交叉验证的损失。
-
type.measure = "deviance",
-
## K = 10 是默认值。
-
nfold = 10,
-
## 多项式回归
-
## ‘alpha = 1’ 是套索惩罚,'alpha=0'是岭惩罚。
-
alpha = 0)
-
## 惩罚vs CV MSE图
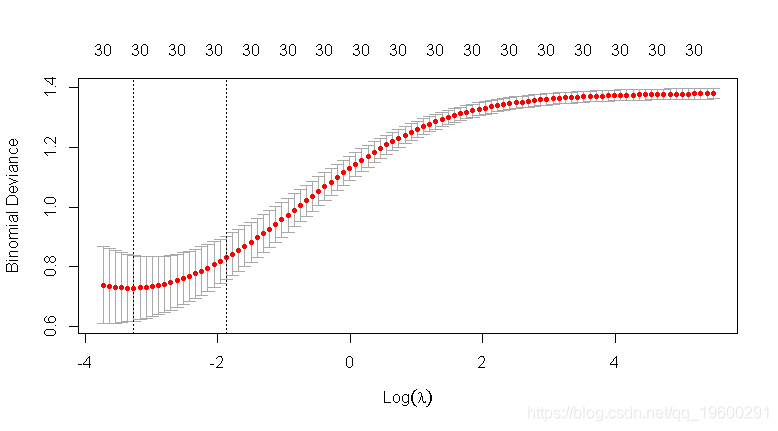
## 在误差最小λ处lambda.min## [1] 0.03488898-
## s:需要进行预测的惩罚参数“lambda”的值。默认值是用于创建模型的整个序列。
-
coef(ridge3_cv, s = lambda.min))
-
## 31 x 1 sparse Matrix of class "dgCMatrix"
-
## 1
-
## (Intercept) 0.1718290283
-
## V1 0.1148574142
-
## V2 0.5068431000
-
## V3 -0.3384649794
-
## V4 -0.8634050979
-
## V5 -0.3141436782
-
## V6 -0.6956355852
-
## V7 0.0798900376
-
## V8 -0.5167458568
-
## V9 0.5193890584
-
## V10 -1.0182682093
-
## V11 -0.2077506627
-
## V12 -0.2218540968
-
## V13 -0.1638673635
-
## V14 0.1370473811
-
## V15 0.0388320169
-
## V16 0.3621440665
-
## V17 -0.1226309533
-
## V18 -0.1492504287
-
## V19 -0.0497939458
-
## V20 -0.2024006258
-
## V21 0.0006531455
-
## V22 0.2456970018
-
## V23 0.4333057414
-
## V24 -0.1769632495
-
## V25 0.5320062623
-
## V26 -0.3875044960
-
## V27 -0.2157079430
-
## V28 0.3337625633
-
## V29 -0.2659968175
-
## V30 0.1601149964
-
## 截距估计应该取消。
-
(best_ridge_coef3)[-1]
-
##执行自适应套索
-
-
## 多项式回归
-
family = "binomial",
-
## “alpha=1”是套索惩罚,“alpha=0”是岭惩罚。
-
alpha = 1,
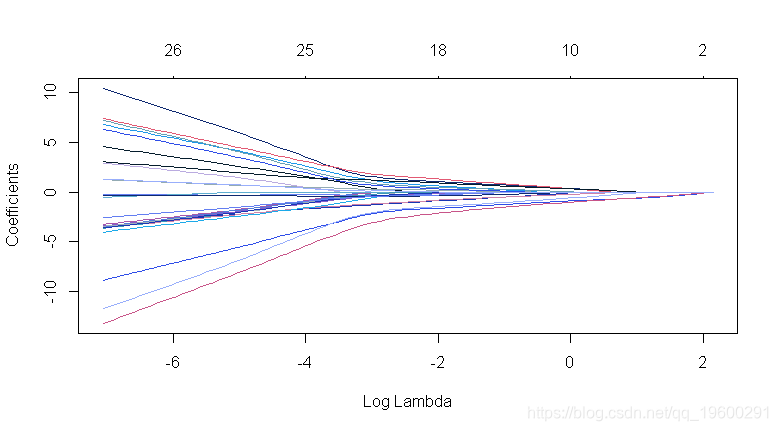
-
## 使用10折CV执行自适应套索
-
## 类型。度量:用于交叉验证的损失。
-
-
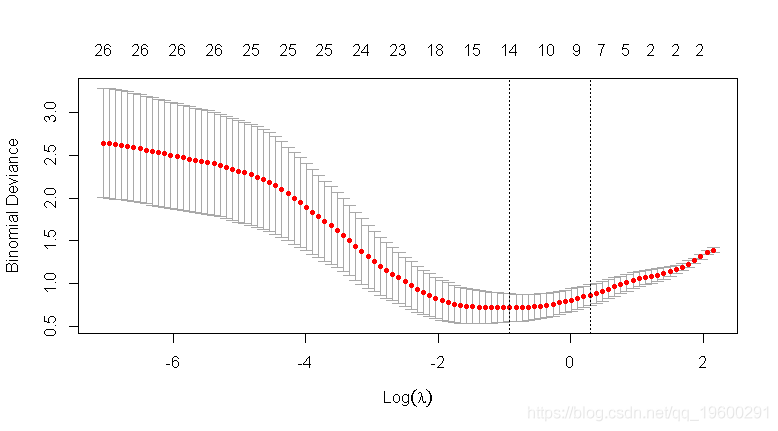
##惩罚vs CV MSE图
-
plot(alasso3_cv)
-
## 在误差最小λ处提取系数
-
lambda.min
## [1] 0.5438827-
## s:需要进行预测的惩罚参数“lambda”的值。默认值是用于创建模型的整个序列。
-
coef(cv, s = lambda.min)
-
## 31 x 1 sparse Matrix of class "dgCMatrix"
-
## 1
-
## (Intercept) 0.19932789
-
## V1 .
-
## V2 0.69081709
-
## V3 -0.48062268
-
## V4 -1.21628612
-
## V5 .
-
## V6 -1.01918155
-
## V7 .
-
## V8 -0.48394892
-
## V9 0.79804285
-
## V10 -1.49657785
-
## V11 .
-
## V12 .
-
## V13 .
-
## V14 .
-
## V15 .
-
## V16 0.19759191
-
## V17 .
-
## V18 .
-
## V19 .
-
## V20 .
-
## V21 .
-
## V22 0.04668665
-
## V23 0.24445410
-
## V24 .
-
## V25 0.57951934
-
## V26 -0.21844124
-
## V27 .
-
## V28 0.07144777
-
## V29 -0.04682770
-
## V30 .
绘制ROC曲线
-
## 提取预测概率和观察结果。
-
pY <- as.(predict(alasso3, newx = x_bin, s = lambda.min, type = "response"))
-
##
-
## 用AUC和阈值绘制ROC曲线
-
plot(roc1)
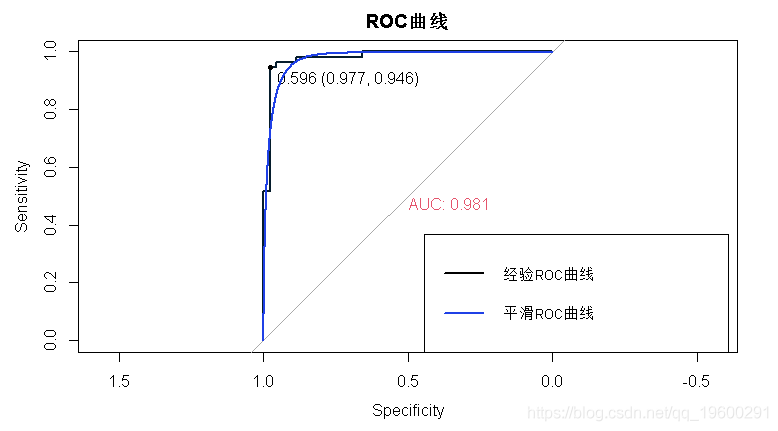
交叉验证测试集AUC
-
lapply(unique(foldid), function(id)
-
## 拟合排除测试集 (foldid == id)
-
-
## 使用模型拟合最佳lambda测试集Yïhat
-
y_pred <- (predict(fit, newx = x_bin[foldid == id], s = lambda.min)
-
## 测试组 Y
-
y <- y_bin[alasso3_cv$foldid == id]
-
## 测试组 AUC
-
roc(y ~ y_pred)$auc
-
## [1] 1.0000000 1.0000000 1.0000000 0.9200000 1.0000000 1.0000000 0.7619048 0.7916667 0.7200000
-
## [10] 0.9375000
## [1] 0.9131071
最受欢迎的见解
3.matlab中的偏最小二乘回归(PLSR)和主成分回归(PCR)
5.R语言回归中的Hosmer-Lemeshow拟合优度检验
▍关注我们
【大数据部落】第三方数据服务提供商,提供全面的统计分析与数据挖掘咨询服务,为客户定制个性化的数据解决方案与行业报告等。
▍咨询链接:http://y0.cn/teradat
▍联系邮箱:3025393450@qq.com



