拓端数据tecdat|R语言中使用非凸惩罚函数回归(SCAD、MCP)分析前列腺数据

原文链接：http://tecdat.cn/?p=20828 

 

本文使用lasso或非凸惩罚拟合线性回归，GLM和Cox回归模型的正则化，特别是最小最大凹度惩罚函数(MCP)和光滑切片绝对偏差惩罚（SCAD），以及其他L2惩罚的选项（ “弹性网络”）。还提供了用于执行交叉验证以及拟合后可视化，摘要，推断和预测的实用程序。

我们研究 前列腺数据，它具有8个变量和一个连续因变量，即将进行根治性前列腺切除术的男性的PSA水平（按对数尺度）：

1.  
    
2.  
   X <- data$X
3.  
   y <- data$y

要将惩罚回归模型拟合到此数据，执行以下操作：

reg(X, y)

此处的默认惩罚是最小最大凹度惩罚函数(MCP)，但也可以使用SCAD和lasso惩罚。这将产生一个系数路径，我们可以绘制

1.  
    
2.  
   plot(fit)

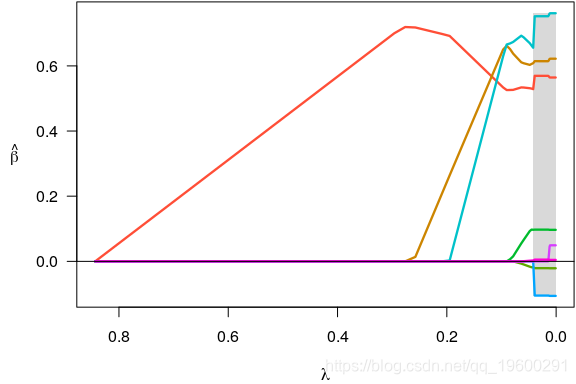
注意，变量一次输入一个模型，并且在λ的任何给定值下，几个系数均为零。要查看系数是多少，我们可以使用以下 coef 函数：

1.  
    
2.  
   coef(fit, lambda=0.05)
3.  
   # (Intercept) lcavol lweight age lbph svi
4.  
   # 0.35121089 0.53178994 0.60389694 -0.01530917 0.08874563 0.67256096
5.  
   # lcp gleason pgg45
6.  
   # 0.00000000 0.00000000 0.00168038

该 summary 方法可用于后选择推断：

1.  
    
2.  
   summary(fit
3.  
   # MCP-penalized linear regression with n=97, p=8
4.  
   # At lambda=0.0500:
5.  
   # -------------------------------------------------
6.  
   # Nonzero coefficients : 6
7.  
   # Expected nonzero coefficients: 2.54
8.  
   # Average mfdr (6 features) : 0.424
9.  
   #
10.  
    # Estimate z mfdr Selected
11.  
    # lcavol 0.53179 8.880 < 1e-04 *
12.  
    # svi 0.67256 3.945 0.010189 *
13.  
    # lweight 0.60390 3.666 0.027894 *
14.  
    # lbph 0.08875 1.928 0.773014 *
15.  
    # age -0.01531 -1.788 0.815269 *
16.  
    # pgg45 0.00168 1.160 0.917570 *

在这种情况下， 即使调整了模型中的其他变量之后，lcavol， svi以及 lweight 显然与因变量关联，同时 lbph， age和 pgg45 可能只是偶然包括。通常，为了评估模型在λ的各种值下的预测准确性，将执行交叉验证：

1.  
    
2.  
   plot(cvfit)

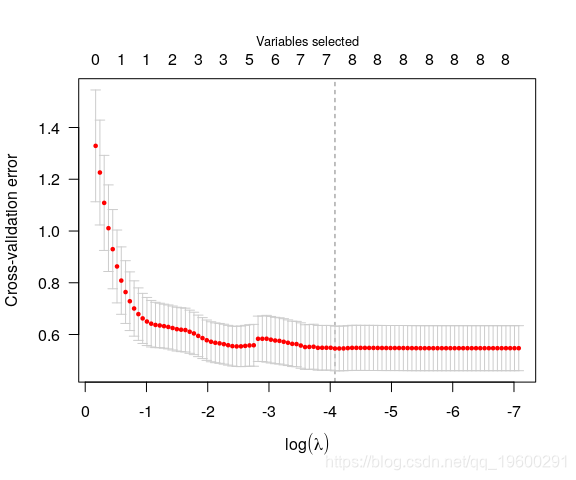
使交叉验证误差最小的λ的值由 cvfit$lambda.min给出，在这种情况下为0.017。将coef 在return的输出 应用于 cv.ncvreg λ的值的系数：

1.  
    
2.  
   coef
3.  
   # (Intercept) lcavol lweight age lbph svi
4.  
   # 0.494154801 0.569546027 0.614419811 -0.020913467 0.097352536 0.752397339
5.  
   # lcp gleason pgg45
6.  
   # -0.104959403 0.000000000 0.005324465

可以通过predict来获得预测值 ，该选项有多种选择：

1.  
    
2.  
   predict(cvfit
3.  
   # 预测新观测结果的响应
4.  
   # 1 2 3 4 5 6
5.  
   # 0.8304040 0.7650906 0.4262072 0.6230117 1.7449492 0.8449595
6.  
    
7.  
   # 非零系数的数量
8.  
   # 0.01695
9.  
   # 7
10.  
     
11.  
    # 非零系数的特性
12.  
    # lcavol lweight age lbph svi lcp pgg45
13.  
    # 1 2 3 4 5 6 8

请注意，原始拟合（至完整数据集）的结果为 cvfit$fit；不必同时调用两者 ncvreg 和 cv.ncvreg 分析数据集。

如， plot(cvfit$fit) 将产生与上述相同的系数路径图 plot(fit) 。

---

最受欢迎的见解

1.R语言多元Logistic逻辑回归 应用案例

2.面板平滑转移回归(PSTR)分析案例实现

3.matlab中的偏最小二乘回归（PLSR）和主成分回归（PCR）

4.R语言泊松Poisson回归模型分析案例

5.R语言回归中的Hosmer-Lemeshow拟合优度检验

6.r语言中对LASSO回归，Ridge岭回归和Elastic Net模型实现

7.在R语言中实现Logistic逻辑回归

8.python用线性回归预测股票价格

9.R语言如何在生存分析与Cox回归中计算IDI，NRI指标