拓端tecdat|R语言Fisher检验探究地区间公寓价格的关系

原文链接：http://tecdat.cn/?p=18927 

 

本文使用波兰公寓价格数据说明Fisher检验。

1.  
    
2.  
   with(data = apart , boxplot(price ~ dis ))

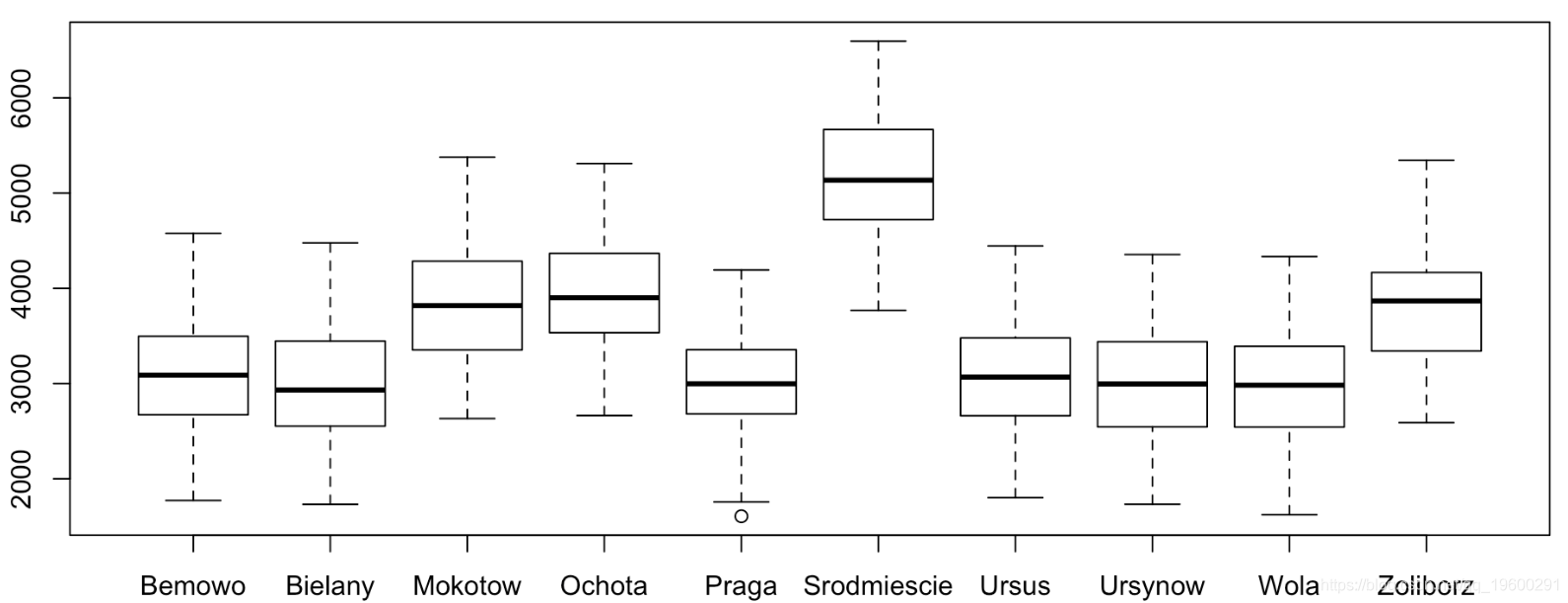
我们在这里对公寓进行分组（这也可以通过简单的回归，这里5个解释变量并不重要）。我们可以重新排列 

A = A[order(A$x),]
 

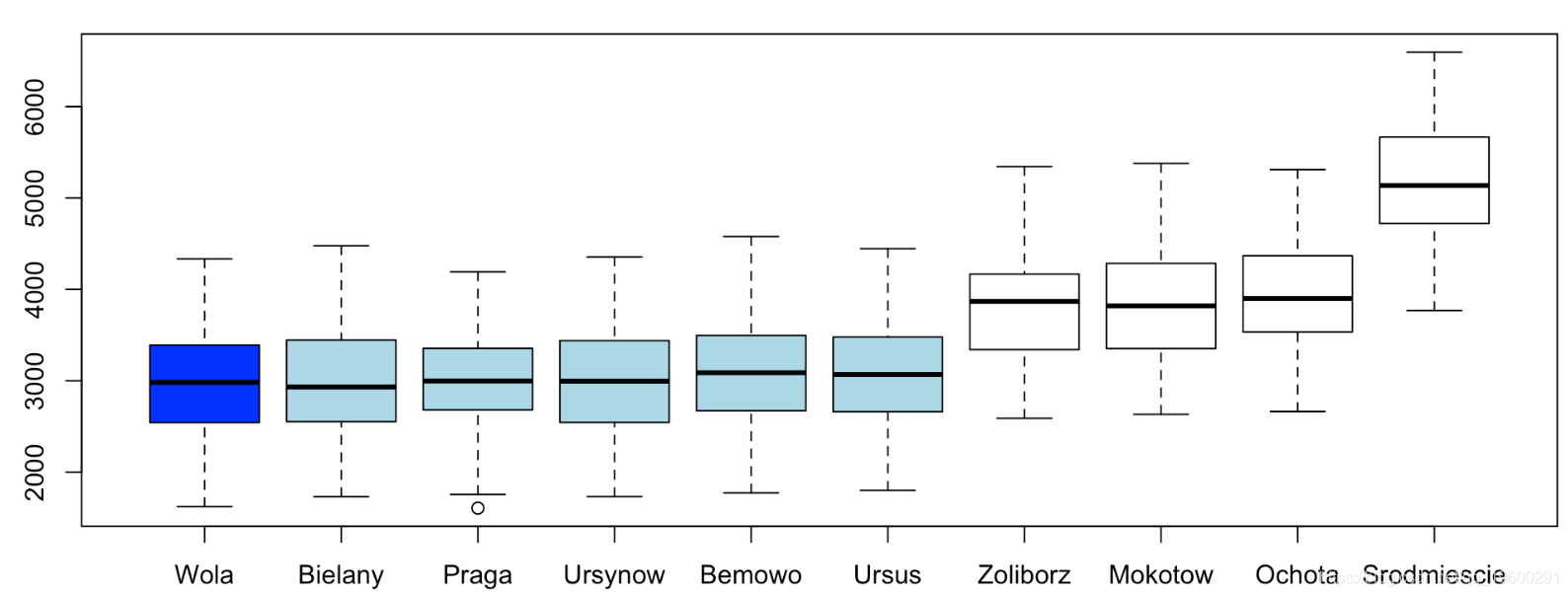
我们以这里最便宜的地区为参考，

1.  
    
2.  
    
3.  
   Coefficients:
4.  
   Estimate Std. Error t value Pr(>|t|)
5.  
   (Intercept) 2968.36 58.02 51.160 <2e-16 ***
6.  
   districtBielany 17.38 84.16 0.207 0.836
7.  
   districtPraga 26.45 85.12 0.311 0.756
8.  
   districtUrsynow 42.01 82.65 0.508 0.611
9.  
   districtBemowo 80.10 83.71 0.957 0.339
10.  
    districtUrsus 102.01 82.25 1.240 0.215
11.  
    districtZoliborz 829.59 83.94 9.884 <2e-16 ***
12.  
    districtMokotow 887.10 81.86 10.837 <2e-16 ***
13.  
    districtOchota 987.93 84.16 11.738 <2e-16 ***
14.  
    districtSrodmiescie 2214.39 83.28 26.591 <2e-16 ***
15.  
    ---
16.  
    Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
17.  
     
18.  
    Residual standard error: 597.4 on 990 degrees of freedom
19.  
    Multiple R-squared: 0.5698, Adjusted R-squared: 0.5659
20.  
    F-statistic: 145.7 on 9 and 990 DF, p-value: < 2.2e-16

我们可以检验前5个地区价格，这是一个多重检验，我们将使用Fisher检验：

1.  
    
2.  
   linHypo(reg, c("districtBielany = 0"
3.  
   "districtPraga = 0"
4.  
   "districtUrsynow = 0"
5.  
   "districtBemowo = 0"
6.  
   "districtUrsus = 0")
7.  
   Linear hypothesis test
8.  
    
9.  
   Model 1: restricted model
10.  
    Model 2: m2.price ~ district
11.  
     
12.  
    Res.Df RSS Df Sum of Sq F Pr(>F)
13.  
    1 995 354051715
14.  
    2 990 353269202 5 782513 0.4386 0.8217

Fisher的统计数据很低，  p值为82％。

1.  
    
2.  
   Linear hypothesis test
3.  
    
4.  
   Model 1: restricted model
5.  
   Model 2: m2.price ~ district
6.  
    
7.  
   Res.Df RSS Df Sum of Sq F Pr(>F)
8.  
   1 996 405455409
9.  
   2 990 353269202 6 52186207 24.374 < 2.2e-16 ***
10.  
    ---
11.  
    Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

我们将对前6种地区进行重组（并称A为地区重组）。如果我们看平均价格，按地区，我们得到

with(data = apar , boxplot( price ~ distr ))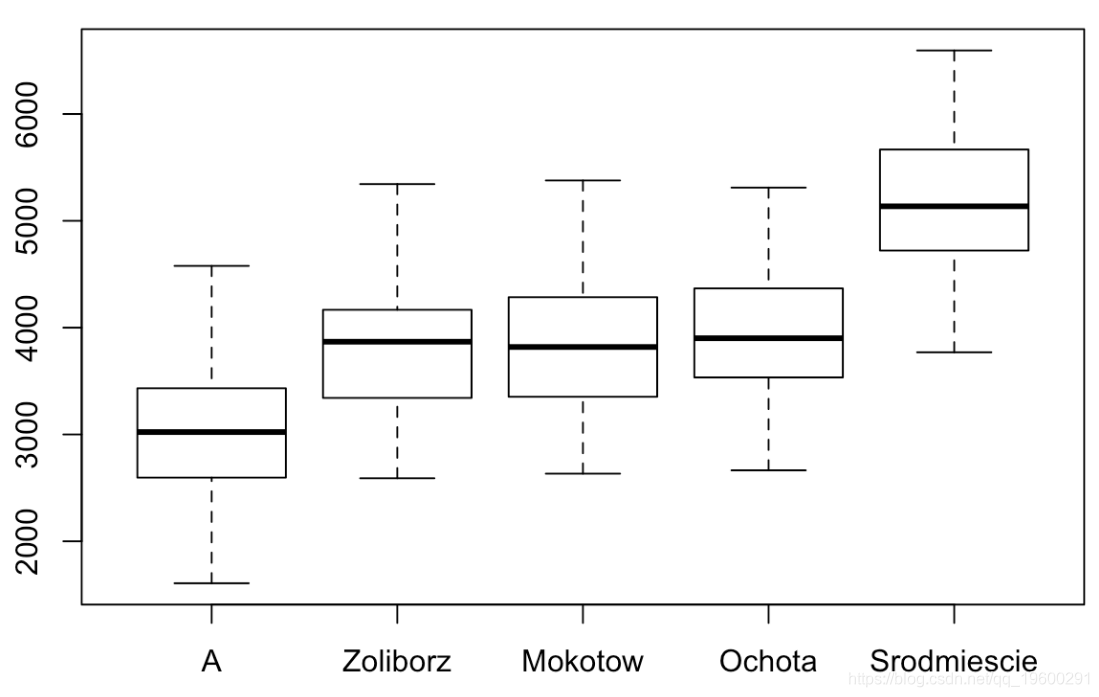

 

我们再次开始，以最便宜的地区作为参考，我们想检验线性回归中接下来的两个地区的系数是否为零。

1.  
    
2.  
   Linear hypothesis test
3.  
    
4.  
   Model 1: restricted model
5.  
   Model 2: m2.price ~ district
6.  
    
7.  
   Res.Df RSS Df Sum of Sq F Pr(<F)
8.  
   1 997 355292524
9.  
   2 995 354051715 2 1240809 1.7435 0.1754

P为0.17，我们可以接受原假设。然后，我们有三组地区，名称分别为A，B和C。我们获得以下框线图

1.  
    
2.  
   with(data = apart , boxplot( price ~ dist ))

 

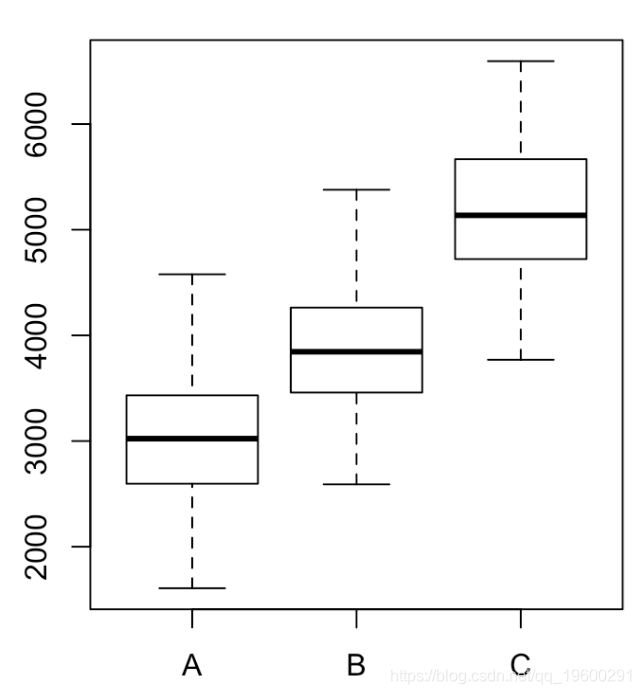
因此，最终我们可以分类成三个不同的地区，如果目标是预测价格，则无需使用10类分类，而3类分类就足够了！

---

最受欢迎的见解

1.Matlab马尔可夫链蒙特卡罗法（MCMC）估计随机波动率（SV，Stochastic Volatility） 模型

2.基于R语言的疾病制图中自适应核密度估计的阈值选择方法

3.WinBUGS对多元随机波动率模型：贝叶斯估计与模型比较

4.R语言回归中的hosmer-lemeshow拟合优度检验

5.matlab实现MCMC的马尔可夫切换ARMA – GARCH模型估计

6.R语言区间数据回归分析

7.R语言WALD检验 VS 似然比检验

8.python用线性回归预测股票价格

9.R语言如何在生存分析与Cox回归中计算IDI，NRI指标