拓端tecdat|R语言混合正态分布极大似然估计和EM算法

原文链接：http://tecdat.cn/?p=18794

 

为了在统计过程中发现更多有趣的结果，我们将解决极大似然估计没有简单分析表达式的情况。举例来说，如果我们混合了各种分布，

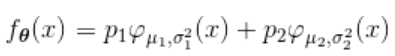
作为说明，我们可以使用样例数据

1.  
    
2.  
   > X=height

第一步是编写混合分布的对数似然函数

1.  
   > logL=function(theta){
2.  
   + p=theta[1]
3.  
   + m1=theta[2]
4.  
   + s1=theta[3]
5.  
   + m2=theta[4]
6.  
   + s2=theta[5]
7.  
   + logL=-sum(log(p*dnorm(X,m1,s1)+(1-p)*dnorm(X,m2,s2)))
8.  
   + return(logL)
9.  
   + }

极大似然性的最简单函数如下（从一组初始参数开始，只是为了获得梯度下降的起点）

1.  
   > optim(c(.5,160,1,180,1 ,logL > theta=opt$par)
2.  
   [1] 0.5987635 165.2547700 5.9410993 178.4856961 6.3547038

因为我们可以通过使用约束优化算法来做到“更好”，例如，概率一定在0到1之间。

为了可视化估计的密度，我们使用

1.  
   > hist(X,col="light green probability=TRUE)
2.  
   > lines(density(X )

 

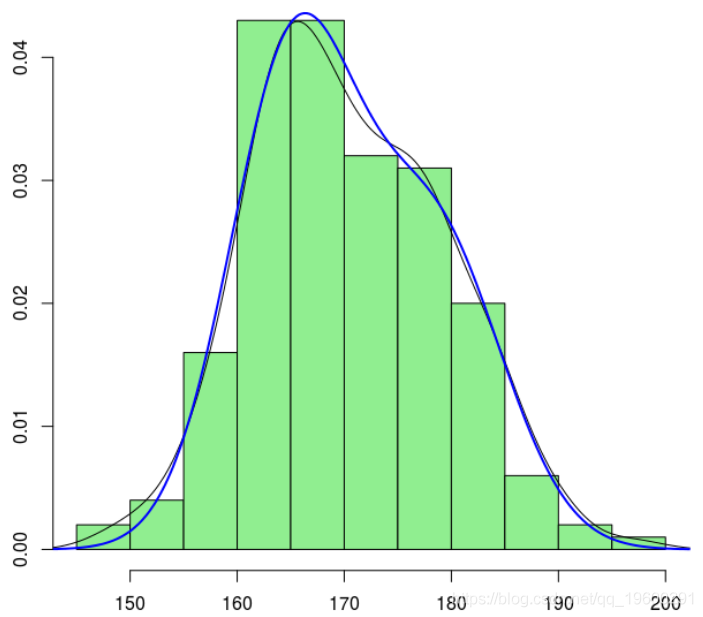
另一个解决方案是使用EM算法。我们将从参数的初始值开始，并比较属于每个类的机会

1.  
    
2.  
   > p=p1/(p1+p2)

从属于每个类别的这些概率中，我们将估算两个正态分布的参数。使用极大似然

1.  
   > m1=sum(p*X)/sum(p)
2.  
    
3.  
   + logL=-sum(log(p*dnorm(X,m1,s1)+(1-p)*dnorm(X,m2,s2)))
4.  
   + return(logL)

这个想法实际上是有一个循环的：我们估计属于这些类的概率（考虑到正态分布的参数），一旦有了这些概率，就可以重新估计参数。然后我们再次开始

1.  
    
2.  
   > for(s in 1:100){
3.  
    
4.  
   + p=p1/(p1+p2)
5.  
    
6.  
   + s1=sqrt(sum(p*(X-m1)^2)/sum(p))
7.  
   + s2=sqrt(sum((1-p)*(X-m2)^2)/sum(1-p))
8.  
    
9.  
   + }

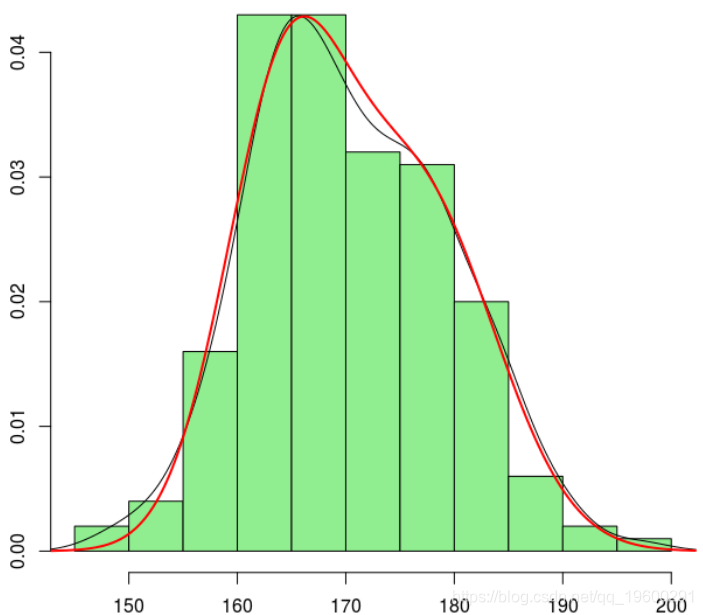
然后，我们恢复混合分布的“最佳”参数

1.  
   > hist(X,col="light green",probability=TRUE)
2.  
   > lines(density(X))

这相对接近我们的估计。

 

---

最受欢迎的见解

1.R语言泊松Poisson回归模型分析案例

2.R语言进行数值模拟：模拟泊松回归模型

3.r语言泊松回归分析

4.R语言对布丰投针（蒲丰投针）实验进行模拟和动态可视化

5.用R语言模拟混合制排队随机服务排队系统

6.GARCH（1,1），MA以及历史模拟法的VaR比较

7.R语言做复杂金融产品的几何布朗运动的模拟

8.R语言进行数值模拟：模拟泊松回归模型

9.R语言对巨灾风险下的再保险合同定价研究案例：广义线性模型和帕累托分布Pareto distributions请选中你要保存的内容，粘贴到此文本框