拓端tecdat|R语言分位数回归Quantile Regression分析租房价格

原文链接：http://tecdat.cn/?p=18422

 

 

本文想在R软件中更好地了解分位数回归优化。在查看分位数回归之前，让我们从样本中计算中位数或分位数。

中位数

考虑一个样本 。要计算中位数，请求解

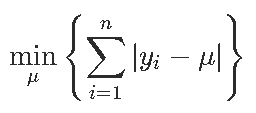
可以使用线性编程技术解决。更确切地说，这个问题等同于

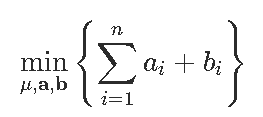
为了说明，考虑对数正态分布的样本，

1.  
   n = 123
2.  
   set.seed(132)
3.  
   y = rlnorm(n)
4.  
   median(y)
5.  
   [1] 1.01523

对于优化问题，使用具有3n个约束和2n + 1参数的矩阵形式，

1.  
    
2.  
   r = lp("min", c(rep(1,2*n),0),
3.  
    
4.  
   tail(r$solution,1)
5.  
   [1] 1.01523

分位数

当然，我们可以将之前的代码改编为分位数

1.  
   tau = .3
2.  
   quantile(x,tau)
3.  
   30%
4.  
   0.674124

线性程序

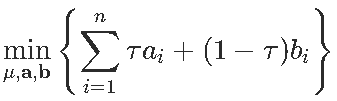
R代码

1.  
    
2.  
   r = lp("min", c(rep(tau,n),rep(1-tau,n),0),
3.  
    
4.  
    
5.  
   [1] 0.674124

 

分位数回归（简单）

考虑一个数据集，该数据集是一个主要城市的单位租金与面积，建筑年龄等的函数。

分位数回归的线性程序

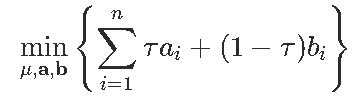
与ai，bi≥0和

在这里使用

1.  
   require(lpSolve)
2.  
    
3.  
   r = lp("min",
4.  
   c(rep(tau,n , rep(1-tau,n),0,0 , rbind(A1, A2 ,
5.  
   c(rep( =", 2*n , rep("=", n) , c(rep(0,2*n), y
6.  
   tail(r$solution,2)
7.  
   [1] 147.845234 3.273453

我们可以使用R函数来拟合该模型

1.  
    
2.  
   rq(ren~are , tau=tau
3.  
   Coefficients:
4.  
   (Intercept) are
5.  
   147.845234 3.273453

我们可以使用不同的概率水平来获得图

1.  
   plot( area, rent,xlab=expression
2.  
   tau = .9
3.  
   r = lp("min",
4.  
   c(re au,n), rep(1-tau rbind(A1 2),
5.  
   c(rep , 2*n), rep("=", n)), c( ,2*n) y))
6.  
    

 

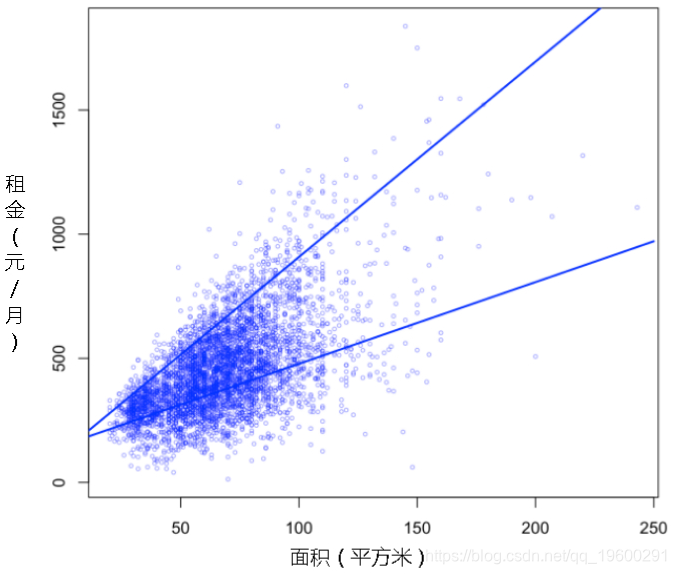
多元分位数回归

现在，我们尝试使用两个协变量呢，例如，让我们看看是否可以将单位的租金解释为面积的（线性）函数和建筑年龄。

1.  
    
2.  
   r = lp("min",
3.  
   c(rep(ta n), rep(1- au,n),0,0, , rbin 1, A2),
4.  
   (r p("& , n), rep("= n)), (rep(0 *n), y))
5.  
   tail(r$sol ,3)
6.  
   [1] 0.000 3.224 0.073

 

1.  
    
2.  
   Coefficients:
3.  
   (Intercept) are year
4.  
   -5322.503252 3.428135 2.637234

结果是完全不同的。可以用IRLS  –迭代加权最小二乘确认后者

1.  
   for(s in 1:500){
2.  
    
3.  
   reg = lm(rent ~area+year ,
4.  
   weigts= tau*(eps t;0 1-tau) eps&lt ))/ s(e ))
5.  
    
6.  
   }
7.  
   reg$coefficients
8.  
   (Intercept) area year
9.  
   -5485.433043 3.932134 2.842943

 

 

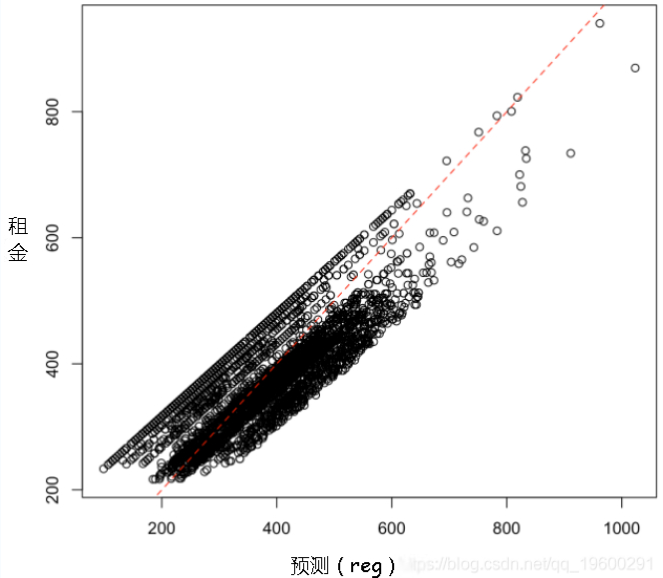
我们可以使后者拟合多元回归，

1.  
    
2.  
   lp("min",c,A consttype,b)
3.  
   beta = r$sol[1:K - r$sol (1:K+K)
4.  
   beta
5.  
   [1] -5542.633252 3.958135 2.857234

与之比较

1.  
    
2.  
   rq(rent~ area + year, tau=tau
3.  
    
4.  
   Coefficients:
5.  
   (Intercept) area yearc
6.  
   -5542.633252 3.958135 2.857234
7.  
    
8.  
   Degrees of freedom: 4571 total; 4568 residual

 

---

最受欢迎的见解

1.R语言多元Logistic逻辑回归 应用案例

2.面板平滑转移回归(PSTR)分析案例实现

3.matlab中的偏最小二乘回归（PLSR）和主成分回归（PCR）

4.R语言泊松Poisson回归模型分析案例

5.R语言回归中的Hosmer-Lemeshow拟合优度检验

6.r语言中对LASSO回归，Ridge岭回归和Elastic Net模型实现

7.在R语言中实现Logistic逻辑回归

8.python用线性回归预测股票价格

9.R语言如何在生存分析与Cox回归中计算IDI，NRI指标