拓端tecdat|R语言:结构方程模型、潜变量分析

原文链接：http://tecdat.cn/?p=3071

结构方程模型入门 

介绍

对于熟悉线性回归拟合结构方程模型的分析师来说，在R环境中，拟合结构方程模型涉及学习新的建模语法，新的绘图语法以及通常是新的数据输入方法。然而，拟合结构方程模型可以成为分析师工具箱中的强大工具。

设置 环境

在R中实现SEM有许多不同的包，lavaan软件包为大多数SEM用户提供了全面的功能集，并且具有易于学习的语法来描述SEM模型。要安装lavaan，我们只需运行：

  1.  
    # 安装
  2.  
    install.packages("lavaan")

读入数据

我们需要读入数据集。我们读取方差 - 协方差矩阵并运行路径分析模型。

  1.  
    mat1 <- matrix(c(1, 0, 0, 0.6, 1, 0, 0.33, 0.63, 1), 3, 3, byrow = TRUE)
  2.  
     
  3.  
     
  4.  
    print(mat1)
  5.  
     
  1.  
    ## ILL IMM DEP
  2.  
    ## ILL 1.00 0.00 0
  3.  
    ## IMM 0.60 1.00 0
  4.  
    ## DEP 0.33 0.63 1
现在我们在我们的环境中命名了一个方差 - 协方差矩阵。

有了这些数据，我们可以构建两种可能的模型

  1. 抑郁症（DEP）影响免疫系统（IMM）影响疾病（ILL）
  2. IMM影响ILL影响DEP

使用SEM我们可以评估哪个模型最能解释我们在上面的数据中观察到的协方差。拟合模型lavaan是一个两步过程。首先，我们创建一个文本字符串定义lavaan模型 。接下来，我们给出lavaan如何拟合这个模型。

  1.  
    # 定义模型
  2.  
     
  3.  
     
  4.  
    # 拟合模型
  5.  
    mod1fit <- sem(mod1, sample.cov = mat1, sample.nobs = 500)
  6.  
     
  7.  
    # 定义模型2
  8.  
     
  9.  
     
  10.  
    mod2fit <- sem(mod2, sample.cov = mat1, sample.nobs = 500)
  11.  
     

现在，我们在环境中为每个模型存储了两个对象。我们有模型字符串和modelfit对象。summary提供输出：

  1.  
    ##
  2.  
    ## Number of observations 500
  3.  
    ##
  4.  
    ## Estimator ML
  5.  
    ## Minimum Function Test Statistic 2.994
  6.  
    ## Degrees of freedom 1
  7.  
    ## P-value (Chi-square) 0.084
  8.  
    ##
  9.  
    ## Parameter estimates:
  10.  
    ##
  11.  
    ## Information Expected
  12.  
    ## Standard Errors Standard
  13.  
    ##
  14.  
    ## Estimate Std.err Z-value P(>|z|)
  15.  
    ## Regressions:
  16.  
    ## ILL ~
  17.  
    ## IMM 0.600 0.036 16.771 0.000
  18.  
    ## IMM ~
  19.  
    ## DEP 0.630 0.035 18.140 0.000
  20.  
    ##
  21.  
    ## Variances:
  22.  
    ## ILL 0.639 0.040
  23.  
    ## IMM 0.602 0.038
  1.  
    ##
  2.  
    ## Number of observations 500
  3.  
    ##
  4.  
    ## Estimator ML
  5.  
    ## Minimum Function Test Statistic 198.180
  6.  
    ## Degrees of freedom 1
  7.  
    ## P-value (Chi-square) 0.000
  8.  
    ##
  9.  
    ## Parameter estimates:
  10.  
    ##
  11.  
    ## Information Expected
  12.  
    ## Standard Errors Standard
  13.  
    ##
  14.  
    ## Estimate Std.err Z-value P(>|z|)
  15.  
    ## Regressions:
  16.  
    ## DEP ~
  17.  
    ## ILL 0.330 0.042 7.817 0.000
  18.  
    ## ILL ~
  19.  
    ## IMM 0.600 0.036 16.771 0.000
  20.  
    ##
  21.  
    ## Variances:
  22.  
    ## DEP 0.889 0.056
  23.  
    ## ILL 0.639 0.040

理解SEM模型的最佳方法之一是使用路径图直观地检查模型。

接下来，我们加载库并制作一些路径图。

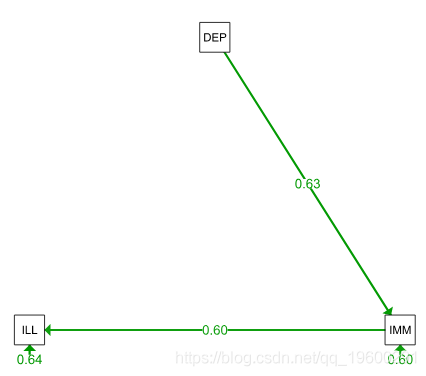
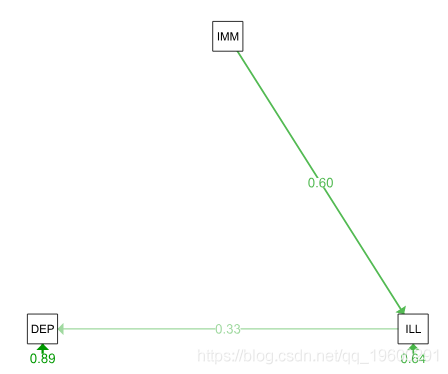
这两个简单的路径模型哪个更好？我们可以运行卡方检验。

  1.  
    ## Chi Square Difference Test
  2.  
    ##
  3.  
    ## Df AIC BIC Chisq Chisq diff Df diff Pr(>Chisq)
  4.  
    ## mod1fit 1 3786 3803 2.99
  5.  
    ## mod2fit 1 3981 3998 198.18 195 0 <2e-16 ***
  6.  
    ## ---
  7.  
    ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

可以看到模型2更好。让我们看一下模型2的一些属性。

# 拟合优度评价指标
  1.  
    ## fmin chisq df pvalue
  2.  
    ## 0.198 198.180 1.000 0.000
  3.  
    ## baseline.chisq baseline.df baseline.pvalue cfi
  4.  
    ## 478.973 3.000 0.000 0.586
  5.  
    ## tli nnfi rfi nfi
  6.  
    ## -0.243 -0.243 1.000 0.586
  7.  
    ## pnfi ifi rni logl
  8.  
    ## 0.195 0.587 0.586 -1986.510
  9.  
    ## unrestricted.logl npar aic bic
  10.  
    ## -1887.420 4.000 3981.020 3997.878
  11.  
    ## ntotal bic2 rmsea rmsea.ci.lower
  12.  
    ## 500.000 3985.182 0.628 0.556
  13.  
    ## rmsea.ci.upper rmsea.pvalue rmr rmr_nomean
  14.  
    ## 0.703 0.000 0.176 0.176
  15.  
    ## srmr srmr_nomean cn_05 cn_01
  16.  
    ## 0.176 0.176 10.692 17.740
  17.  
    ## gfi agfi pgfi mfi
  18.  
    ## 0.821 -0.075 0.137 0.821
  19.  
    ## ecvi
  20.  
    ## 0.412
  1.  
     
  2.  
    # 模型参数预测
  1.  
    ## lhs op rhs est se z pvalue ci.lower ci.upper
  2.  
    ## 1 DEP ~ ILL 0.330 0.042 7.817 0 0.247 0.413
  3.  
    ## 2 ILL ~ IMM 0.600 0.036 16.771 0 0.530 0.670
  4.  
    ## 3 DEP ~~ DEP 0.889 0.056 15.811 0 0.779 1.000
  5.  
    ## 4 ILL ~~ ILL 0.639 0.040 15.811 0 0.560 0.718
  6.  
    ## 5 IMM ~~ IMM 0.998 0.000 NA NA 0.998 0.998
  1.  
     
  2.  
    # 修改指标
  3.  
    ## lhs op rhs mi epc sepc.lv sepc.all sepc.nox
  4.  
    ## 1 DEP ~~ DEP 0.0 0.000 0.000 0.000 0.000
  5.  
    ## 2 DEP ~~ ILL 163.6 -0.719 -0.719 -0.720 -0.720
  6.  
    ## 3 DEP ~~ IMM 163.6 0.674 0.674 0.675 0.674
  7.  
    ## 4 ILL ~~ ILL 0.0 0.000 0.000 0.000 0.000
  8.  
    ## 5 ILL ~~ IMM NA NA NA NA NA
  9.  
    ## 6 IMM ~~ IMM 0.0 0.000 0.000 0.000 0.000
  10.  
    ## 7 DEP ~ ILL 0.0 0.000 0.000 0.000 0.000
  11.  
    ## 8 DEP ~ IMM 163.6 0.675 0.675 0.675 0.676
  12.  
    ## 9 ILL ~ DEP 163.6 -0.808 -0.808 -0.808 -0.808
  13.  
    ## 10 ILL ~ IMM 0.0 0.000 0.000 0.000 0.000
  14.  
    ## 11 IMM ~ DEP 143.8 0.666 0.666 0.666 0.666
  15.  
    ## 12 IMM ~ ILL 0.0 0.000 0.000 0.000 0.000

非常感谢您阅读本文，有任何问题请在下面留言！

最受欢迎的见解

1.R语言多元Logistic逻辑回归 应用案例

2.面板平滑转移回归(PSTR)分析案例实现

3.matlab中的偏最小二乘回归（PLSR）和主成分回归（PCR）

4.R语言泊松Poisson回归模型分析案例

5.R语言回归中的Hosmer-Lemeshow拟合优度检验

6.r语言中对LASSO回归，Ridge岭回归和Elastic Net模型实现

7.在R语言中实现Logistic逻辑回归

8.python用线性回归预测股票价格

9.R语言如何在生存分析与Cox回归中计算IDI，NRI指标

posted @ 2020-12-10 23:16  拓端tecdat  阅读(372)  评论(0)  编辑  收藏  举报