拓端tecdat|R语言辅导中的多项式回归、B样条曲线(B-spline Curves)回归
原文链接:http://tecdat.cn/?p=18129
在线性模型的文章中,我们已经了解了如何在给出协变量x的向量时构造线性模型。但更一般而言,我们可以考虑协变量的变换,来使用线性模型。
我们首先讨论多项式回归,进一步,我们会想到分段线性或分段多项式函数,可能还有附加的连续性约束,这些是样条曲线回归的基础。
多项式回归
谈论多项式回归时(在单变量情况下)
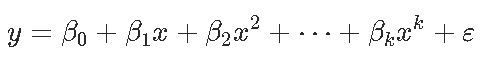
我们使用
-
coef = leg.poly(n=4)
-
[[1]]
-
1
-
-
[[2]]
-
x
-
-
[[3]]
-
-0.5 + 1.5*x^2
-
-
[[4]]
-
-1.5*x + 2.5*x^3
-
-
[[5]]
-
0.375 - 3.75*x^2 + 4.375*x^4
有许多正交多项式族(Jacobi多项式, Laguerre多项式, Hermite多项式等)。在R中有用于多项式回归的标准多边形函数。
当使用poly时,我们使用矩阵的 QR分解。我们使用
-
poly - function (x, deg = 1) {
-
xbar = mean(x)
-
x = x - xbar
-
QR = qr(outer(x, 0:degree, "^"))
-
X = qr.qy(QR, diag(diag(QR$qr),
这两个模型是等效的。
-
-
dist~speed+I(speed^2)+I(speed^3)
-
dist~poly(speed,3)
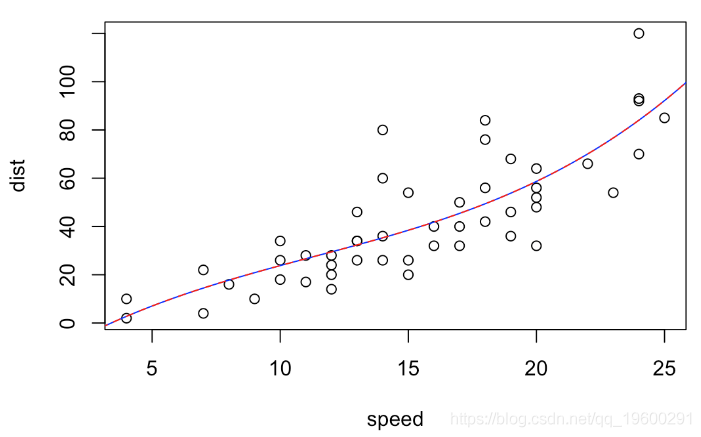
我们有完全相同的预测
-
-
v1[u==15]
-
121
-
38.43919
-
v2[u==15]
-
121
-
38.43919
系数没有相同的解释,但是p值完全相同,两个模型以相同的置信度拒绝三次多项式,
-
summary(reg1)
-
-
Coefficients:
-
Estimate Std. Error t value Pr(>|t|)
-
(Intercept) -19.50505 28.40530 -0.687 0.496
-
speed 6.80111 6.80113 1.000 0.323
-
I(speed^2) -0.34966 0.49988 -0.699 0.488
-
I(speed^3) 0.01025 0.01130 0.907 0.369
-
-
Residual standard error: 15.2 on 46 degrees of freedom
-
Multiple R-squared: 0.6732, Adjusted R-squared: 0.6519
-
F-statistic: 31.58 on 3 and 46 DF, p-value: 3.074e-11
-
-
summary(reg2)
-
-
Coefficients:
-
Estimate Std. Error t value Pr(>|t|)
-
(Intercept) 42.98 2.15 19.988 < 2e-16 ***
-
poly(speed, 3)1 145.55 15.21 9.573 1.6e-12 ***
-
poly(speed, 3)2 23.00 15.21 1.512 0.137
-
poly(speed, 3)3 13.80 15.21 0.907 0.369
-
---
-
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
-
-
Residual standard error: 15.2 on 46 degrees of freedom
-
Multiple R-squared: 0.6732, Adjusted R-squared: 0.6519
-
F-statistic: 31.58 on 3 and 46 DF, p-value: 3.074e-11
B样条曲线(B-spline curve)和GAM
样条曲线在回归模型中也很重要,尤其是当我们开始讨论 广义加性模型时。在单变量情况下,我通过引入(线性)样条曲线,
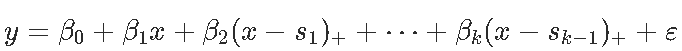
模型是连续的(连续函数的加权总和是连续的)。我们可以进一步
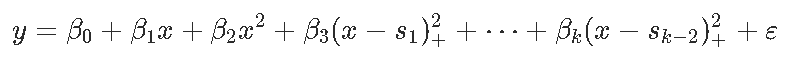
二次样条
用于三次样条。有趣的是,二次样条不仅是连续的,而且它们的一阶导数也是连续的(三次样条是连续的)。这些模型易于解释。例如,简单的模型
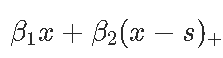
是以下连续的分段线性函数,在节点s处分段。
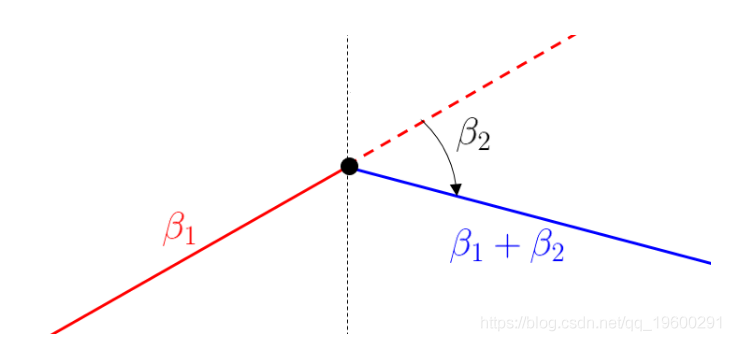
还应遵守以下解释:对于xx较小的值,线性增加,斜率\beta_1β1\;对于xx较大的值,线性减小,斜率\ beta_1 + \beta_2β1+β2。因此,\beta_2β2被解释为斜率的变化。
现在在R中使用bs函数(即标准B样条)并可视化
-
-
x = seq(5,25,by=.25)
-
B = bs(x,knots=c(10,20),Boundary.knots=c(5,55),degre=1)
-
matplot(x,B,type="l",lty=1,lwd=2,col=clr6)
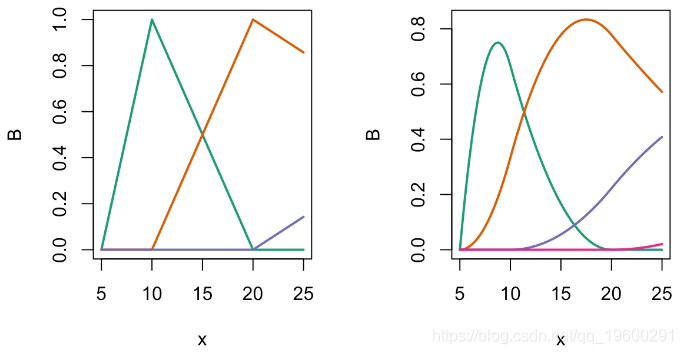
提到的函数如下
-
-
par(mfrow=c(1,2))
-
-
matplot(x,B,type="l",lty=1,lwd=2)
-
-
matplot(x,B,type="l",col=clr)
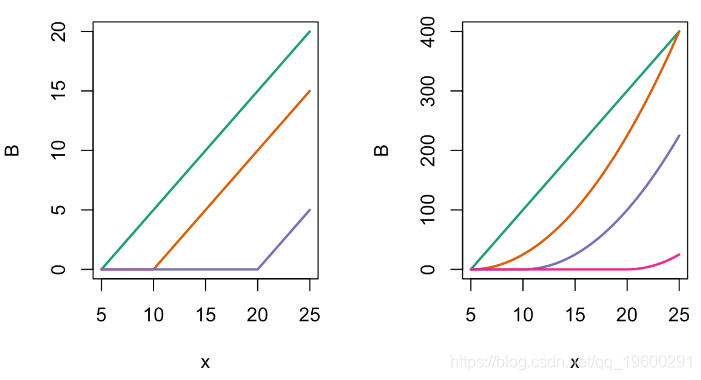
多项式回归中这两个模型表示方法是等效的。例如
-
dist~speed+pos(speed,10)+pos(speed,20
-
dist~bs(speed,degree=1,knots=c(10,20)
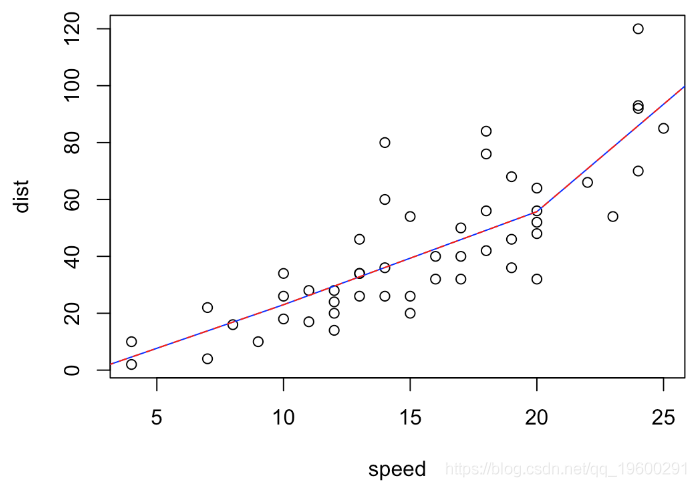
-
v1[u==15]
-
121
-
39.35747
-
v2[u==15]
-
121
-
39.35747
这两个模型以及系数的解释是等效的:
-
summary(reg1)
-
-
Coefficients:
-
Estimate Std. Error t value Pr(>|t|)
-
(Intercept) -7.6305 16.2941 -0.468 0.6418
-
speed 3.0630 1.8238 1.679 0.0998 .
-
pos(speed, 10) 0.2087 2.2453 0.093 0.9263
-
pos(speed, 20) 4.2812 2.2843 1.874 0.0673 .
-
---
-
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
-
-
Residual standard error: 15 on 46 degrees of freedom
-
Multiple R-squared: 0.6821, Adjusted R-squared: 0.6613
-
F-statistic: 32.89 on 3 and 46 DF, p-value: 1.643e-11
-
-
summary(reg2)
-
-
Coefficients:
-
Estimate Std. Error t value Pr(>|t|)
-
(Intercept) 4.621 9.344 0.495 0.6233
-
bs(speed, degree = 1, knots = c(10, 20))1 18.378 10.943 1.679 0.0998 .
-
bs(speed, degree = 1, knots = c(10, 20))2 51.094 10.040 5.089 6.51e-06 ***
-
bs(speed, degree = 1, knots = c(10, 20))3 88.859 12.047 7.376 2.49e-09 ***
-
---
-
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
-
-
Residual standard error: 15 on 46 degrees of freedom
-
Multiple R-squared: 0.6821, Adjusted R-squared: 0.6613
-
F-statistic: 32.89 on 3 and 46 DF, p-value: 1.643e-11
在这里我们可以直接看到,第一个结点的斜率没有明显变化。

最受欢迎的见解
3.matlab中的偏最小二乘回归(PLSR)和主成分回归(PCR)
5.R语言回归中的Hosmer-Lemeshow拟合优度检验
6.r语言中对LASSO回归,Ridge岭回归和Elastic Net模型实现
9.R语言如何在生存分析与Cox回归中计算IDI,NRI指标





