拓端tecdat|R语言中使用RCPP并行计算指数加权波动率

原文链接：http://tecdat.cn/?p=17829

 

指数加权波动率是一种波动率的度量，它使最近的观察结果有更高权重。我们将使用以下公式计算指数加权波动率：

S [t] ^ 2 = SUM（1-a）* a ^ i *（r [t-1-i]-rhat [t]）^ 2，i = 0…inf

其中rhat [t]是对应的指数加权平均值

rhat [t] = SUM（1-a）* a ^ i * r [t-1-i]，i = 0…inf

上面的公式取决于每个时间点的完整价格历史记录，并花了一些时间进行计算。因此，我想分享Rcpp和RcppParallel如何帮助我们减少计算时间。

我将使用汇率的历史数据集  作为测试数据。

首先，我们计算平均滚动波动率

1.  
   #*****************************************************************
2.  
   # 计算对数收益率
3.  
   #*****************************************************************
4.  
   ret = diff(log(data$prices))
5.  
    
6.  
   tic(5)
7.  
   hist.vol = sqrt(252) * bt.apply.matrix(ret, runSD, n = 200)
8.  
   toc(5)

经过时间为0.17秒

接下来，让我们编写指数加权代码逻辑

1.  
   # 建立 RCPP 函数计算指数加权波动率
2.  
   load.packages('Rcpp')
3.  
   sourceCpp(code='
4.  
   #include <Rcpp.h>
5.  
   using namespace Rcpp;
6.  
   using namespace std;
7.  
    
8.  
   // [[Rcpp::plugins(cpp11)]]
9.  
    
10.  
    //ema[1] = 0
11.  
    //ema[t] = (1-a)*r[t-1] + (1-a)*a*ema[t-1]
12.  
    // [[Rcpp::exp
13.  
     
14.  
    {
15.  
    if(!NumericVector::is_na(x[t])) break;
16.  
    res[t] = NA_REAL;
17.  
    }
18.  
    int start_t = t;
19.  
     
20.  
    -a) * a^i * (r[t-1-i] - rhat[t])^2, i=0 ... inf
21.  
    // [[Rcpp::export]]
22.  
    NumericVector run_esd_cpp(NumericVector x, double ratio) {
23.  
    auto sz = x.siz
24.  
     
25.  
    // find start index; first non NA item
26.  
    for(t = 0; t < sz; t++) {
27.  
    if(!Num
28.  
    0;
29.  
    for(t = start_t + 1; t < sz; t++) {
30.  
    ema = (1-ratio) * ( x[t-1] + ratio * ema);
31.  
    double sigma = 0;
32.  
    for(int i = 0; i < (t - start_t); i++) {
33.  
    sigma += pow(ratio,i) * pow(x[t-1-i] - ema, 2);
34.  
    }
35.  
    res[t] = (1-ratio) * sigma;
36.  
    }
37.  
    , n, ratio = n/(n+1)) run_ema_cpp(x, ratio)
38.  
    run.esd = funct

 经过时间为106.16秒。

执行此代码花了一段时间。但是，代码可以并行运行。以下是RcppParallel版本。

1.  
   # 建立 RCPP 并行函数计算指数加权波动率
2.  
   load.packages('RcppParallel')
3.  
   sourceCpp(code='
4.  
    
5.  
   using namespace Rcpp;
6.  
   using namespace s
7.  
   s(cpp11)]]
8.  
   // [[Rcpp::depends(R
9.  
   to read from
10.  
    const RMatrix<double> mat;
11.  
    // internal variables
12.  
    const double ratio
13.  
    t;
14.  
    // initialize from Rcpp input and output matrixes
15.  
    run_esd_helper(const Nume
16.  
    all operator that work for th
17.  
     
18.  
    in, size_t end) {
19.  
    for (size_t c1 = begin; c1 < end; c1++) {
20.  
    int t;
21.  
    // find start index; fir

经过时间为14.65秒

运行时间更短。接下来，让我们直观地了解使用指数加权波动率的影响

1.  
   dates = '2007::2010'
2.  
   layout(1:2)
3.  
   e='h', col='black', plotX=F)
4.  
   plota.legend(paste('Dai
5.  
   s,1],type='l',col='black')
6.  
    
7.  
    
8.  
    

 

 

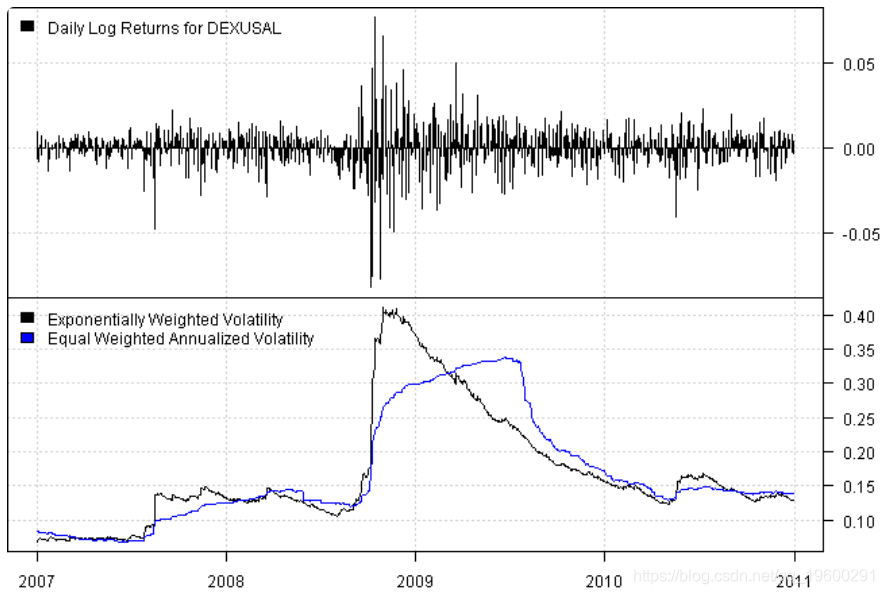
不出所料，指数加权波动率在最近的观察结果中占了更大的比重，是一种更具反应性的风险度量。

---

最受欢迎的见解

1.HAR-RV-J与递归神经网络（RNN）混合模型预测和交易大型股票指数的高频波动率

2.WinBUGS对多元随机波动率模型：贝叶斯估计与模型比较

3.波动率的实现：ARCH模型与HAR-RV模型

4.R语言ARMA-EGARCH模型、集成预测算法对SPX实际波动率进行预测

5.使用R语言随机波动模型SV处理时间序列中的随机波动率

6.R语言多元COPULA GARCH 模型时间序列预测

7.R语言基于ARMA-GARCH过程的VAR拟合和预测

8.R语言随机搜索变量选择SSVS估计贝叶斯向量自回归（BVAR）模型

9.R语言对S＆P500股票指数进行ARIMA + GARCH交易策略