拓端tecdat|R语言具有Student-t分布改进的GARCH（1,1）模型的贝叶斯估计

原文链接：http://tecdat.cn/?p=17494

本说明介绍了具有Student-t改进的GARCH（1,1）模型的贝叶斯估计方法。

介绍

摘要

本说明介绍使用Student-t改进的GARCH（1,1）模型对汇率对数收益进行贝叶斯估计。

自Engle（1982）的开创性论文以来，使用时间序列模型改变波动率的研究一直很活跃。ARCH（自回归条件异方差）和GARCH（广义ARCH）类型模型迅速发展成为80年代预测波动率的经验模型的丰富家族。这些模型是金融计量经济学的广泛传播和必不可少的工具。在Bollerslev（1986）引入的GARCH（p，q）模型中，（金融资产或金融指数）对数收益yt在时间t的条件方差假设用ht表示，它是过去q个对数返回和过去p个条件方差的平方的线性函数。更确切地说：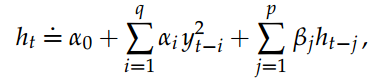

带有Student-t改进的GARCH（1,1）模型基于Nakatsuma（1998）的工作，由Metropolis-Hastings（MH）算法组成，其中分布是根据平方观测值由辅助ARMA过程构建的。这种方法避免了选择和调整采样算法的耗时且困难的任务，特别是对于非专家而言。该程序用R编写，带有一些用C实现的子例程，以加快仿真过程。该算法的有效性以及计算机代码的正确性已通过Geweke（2004）的方法进行了验证。

模型，先验和MCMC方案

可以通过数据扩充编写具有Student-t改进的GARCH（1,1）模型，用于对数收益率fytg。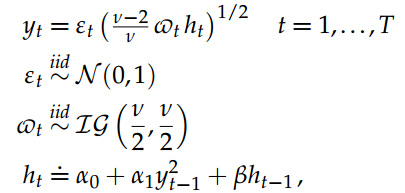

我们强调以下事实：在MH算法中仅实现正约束。在仿真过程中没有施加平稳性条件。

为了编写似然函数，我们定义向量y =（y1，...，yT）0，v =（v1，...，vT）0和a =（.a0，a1）。我们将模型参数重新组合为向量y =（.a，b，n）。然后，在定义T×T对角矩阵时

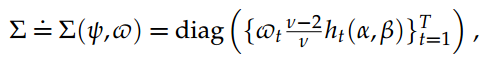
我们可以将（y，v）表示为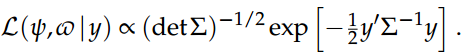

贝叶斯方法将（y，v）视为随机变量，其特征在于以p（y，v）表示的先验密度。先验是在称为超参数的参数的帮助下指定的，这些参数最初假定为已知且恒定。而且，根据研究人员的先验信息，这种密度可能或多或少地提供信息。然后，通过将模型参数的似然函数与先验密度耦合，我们可以使用贝叶斯规则对概率密度进行变换，以得出后验密度p（y，vjy），如下所示：

该后验是观察数据后关于模型参数的知识的定量概率描述。
我们在GARCH参数a和b上使用了截距的普通先验

其中m•和S•是超参数，1f·g是指标函数，fNd是d维法向密度。可以发现以n为条件的向量v的先验分布，从而得出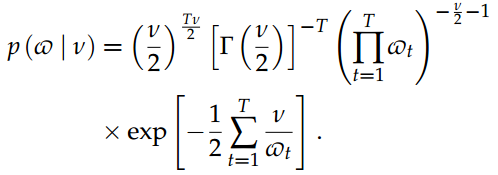

在选择自由度参数的先验分布时，我们遵循Deschamps（2006）的方法。分布是参数l> 0且d≥2的平移指数

对于较大的l值，先验质量集中在d附近，并且可以通过这种方式对自由度施加约束。

实现的MCMC采样基于Ardia（2008）的方法，该方法的灵感来自Nakatsuma（1998）的先前工作。该算法由MH算法组成，其中GARCH参数按块更新（a对应一个块，b对应一个块），而自由度参数是使用优化的拒绝技术从转换后的指数源密度中采样的。该方法具有全自动的优点。

实例分析

我们将贝叶斯估计方法应用于（DEM / GBP）外汇对数收益率的每日观察值。样本时间为1985年1月3日至1991年12月31日，共1974个观测值。此数据集已被推广为GARCH时间序列软件验证的非正式基准。从这个时间序列中，前750个观测值用于说明贝叶斯方法。我们的数据集中的观察窗口摘录绘制在图1中。

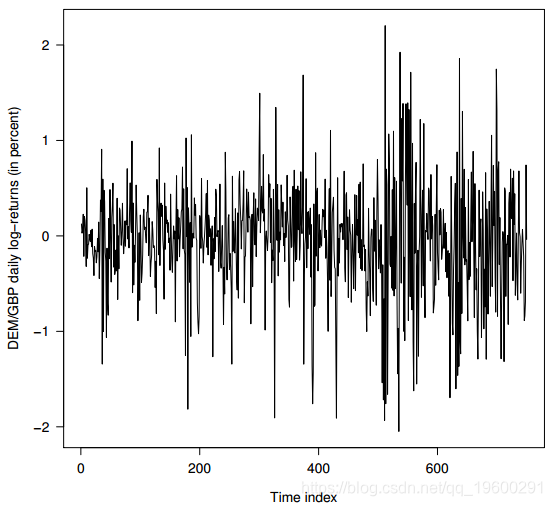
我们对带有Student-t的GARCH（1,1）模型进行了改进，以拟合此观察窗的数据

function (y, mu.alpha = c(0, 0),
Sigma.alpha = 1000 * diag(1,2),
mu.beta = 0, Sigma.beta = 1000,
lambda = 0.01, delta = 2,
control = list())

函数的输入自变量是数据向量，超参数，例如：
• 要生成的MCMC链数；默认值1。
• 每个MCMC链的长度；•start.val：链的起始值的向量；默认值为10000 。
作为贝叶斯估计的先验分布。通过设置控制参数值n.chain = 2和l.chain = 5000，我们为5000次传递生成了两条链。

> MCMC <- bayg(y, control = list(
l.chain = 5000, n.chain = 2))
chain: 1 iteration: 10
parameters: 0.0441 0.212 0.656 115
chain: 1 iteration: 20
parameters: 0.0346 0.136 0.747 136
...
chain: 2 iteration: 5000
parameters: 0.0288 0.190 0.754 4.67

生成MCMC链的跟踪图（即，迭代与采样值的图）。采样器的收敛（使用Gelman和Rubin（1992）的诊断测试），链中的接受率和自相关可以如下计算：

diag
Point est. 97.5% quantile
alpha0 1.02 1.07
alpha1 1.01 1.05
beta 1.02 1.07
nu 1.02 1.06
Multivariate psrf
1.02
> 1 - rejectionRate
alpha0 alpha1 beta nu
0.890 0.890 0.953 1.000
>
autocorr.diag
alpha0 alpha1 beta nu
Lag 0 1.000 1.000 1.000 1.000
Lag 1 0.914 0.872 0.975 0.984
Lag 5 0.786 0.719 0.901 0.925
Lag 10 0.708 0.644 0.816 0.863
Lag 50 0.304 0.299 0.333 0.558

收敛诊断没有显示最后2500次迭代的收敛证据。MCMC采样算法的接受率非常高，从向量a的89％到b的95％不等，这表明分布接近于全部条件。我们丢弃了从MCMC的整体输出中抽样前2500次作为预烧期，仅保留第二次抽样以减少自相关，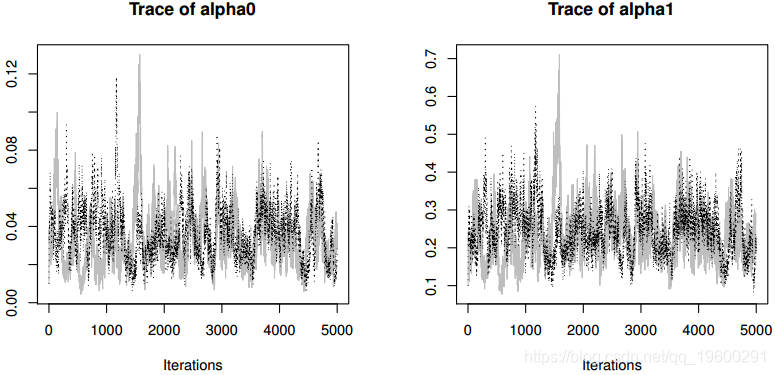

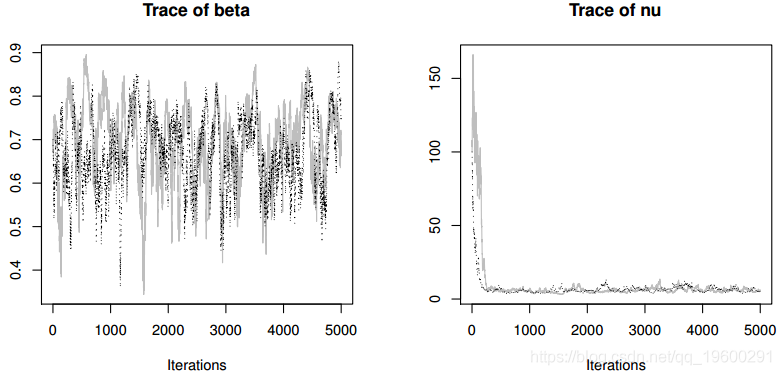
> smpl
n.chain : 2
l.chain : 5000
l.bi : 2500
batch.size: 2
smpl size : 2500

基本的后验统计：

Iterations = 1:2500
Thinning interval = 1
Number of chains = 1
Sample size per chain = 2500
1. Empirical mean and standard deviation
for each variable, plus standard error
of the mean:

Mean SD Naive SE Time-series SE
alpha0 0.0345 0.0138 0.000277 0.00173
alpha1 0.2360 0.0647 0.001293 0.00760
beta 0.6832 0.0835 0.001671 0.01156
nu 6.4019 1.5166 0.030333 0.19833

每个变量的分位数：

2.5% 25% 50% 75% 97.5%
alpha0 0.0126 0.024 0.0328 0.0435 0.0646
alpha1 0.1257 0.189 0.2306 0.2764 0.3826
beta 0.5203 0.624 0.6866 0.7459 0.8343
nu 4.2403 5.297 6.1014 7.2282 10.1204

通过首先将输出转换为矩阵，然后使用函数hist，可以获取模型参数的边际分布。

边缘后部密度显示在图3中。我们清楚地注意到直方图的不对称形状。对于参数n尤其如此。后平均值和中位数之间的差异也反映了这一点。这些结果应该警告我们，不要滥用渐近论证。在当前情况下，即使是750次观测也不足以证明参数估计量分布的渐近对称正态近似。
可以通过从联合后验样本中进行仿真来直接获得关于模型参数的非线性函数的概率陈述。
特别是，我们可以测试协方差平稳性条件，并在满足该条件时估计无条件方差的密度。根据GARCH（1,1）规范，如果a1 + b <1，则过程是协方差平稳的。值接近1时，过去的冲击和过去的方差将对未来的条件方差产生更长的影响。
为了推断平方过程的持久性，我们仅使用后验样本，并为后验样本中的每个绘制y [j]生成（a1 [j] + b [j]）。持久性的后部密度绘制在图4中。直方图向左倾斜，中值为0.923，最大值为1.050。假设a1 + b <1，则GARCH（1,1）模型的无条件方差为a0 /（1- a1- b）。条件是存在时，后验均值为0.387，90％可信区间为[0.274,1.378 ]。经验方差为0.323。

使用联合后验样本可以获得关于模型参数的其他概率陈述。使用后验样本，我们估计条件峰度存在的后验概率为0.994。在存在条件下，峰度的后均值为8.21，中位数为5.84，对区间的95％置信度为[4.12,15.81]，表明尾部比正态分布更重。条件峰度的后验正偏是由几个非常大的值（最大模拟值为404.90）引起的。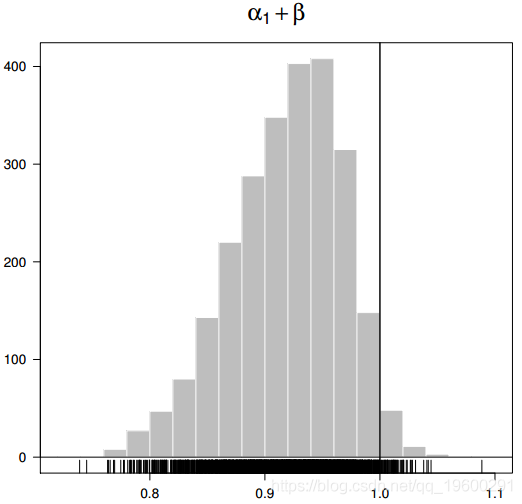

先前的限制和常规改进

控制参数addPriorConditions可用于在估计期间对模型参数y施加任何类型的约束。例如，为了确保估计协方差平稳GARCH（1,1）模型，应将函数定义为

p<-function(psi)
+ psi[2] + psi[3] < 1

实用建议

该算法中实施的估算策略是全自动的，不需要对MCMC采样器进行任何调整。对于从业者来说，这无疑是一个吸引人的功能。但是，马尔可夫链的生成非常耗时，因此每天在多个数据集上估算模型可能会花费大量时间。在这种情况下，通过在多个处理器上运行单链可以轻松地使算法并行化。例如，可以使用foreach包轻松实现此目标（Revolution Computing，2010）。同样，当估计值在更新的时间序列（即具有最近观测值的时间序列）上重复时，明智的做法是使用在前一个估计步骤获得的参数的后验均值或中值来启动算法。初始值（预烧阶段）的影响可能较小，因此收敛速度更快。最后，请注意，与任何MH算法一样，采样器可能会卡在给定的值上，因此链不再移动。

总结

本说明介绍了Student-t改进对GARCH（1,1）模型的贝叶斯估计。我们举例说明了在汇率对数收益率上的实证应用。

参考书目

D. Ardia 使用GARCH模型的贝叶斯估计进行的金融风险管理：理论与应用，经济学和数学系统讲义第612卷。Springer-Verlag，德国柏林，2008年6月。ISBN978-3-540-78656-6。网址http://www.springer.com/economics/econometrics/book/978-3-540-78656-6。