拓端tecdat|R语言使用bootstrap和增量法计算广义线性模型(GLM)预测置信区间
原文链接:http://tecdat.cn/?p=15062

考虑简单的泊松回归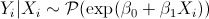 。给定的样本
。给定的样本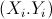 ,其中
,其中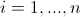
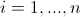 ,目标是导出用于一个95%的置信区间
,目标是导出用于一个95%的置信区间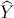 给出
给出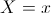 ,其中
,其中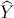 是预测。
是预测。
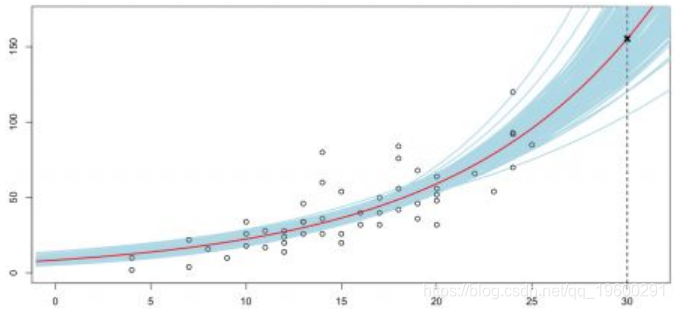
因此,我们要导出预测的置信区间,而不是观测值,即下图的点
-
> r=glm(dist~speed,data=cars,family=poisson)
-
> P=predict(r,type="response",
-
+ newdata=data.frame(speed=seq(-1,35,by=.2)))
-
> plot(cars,xlim=c(0,31),ylim=c(0,170))
-
> abline(v=30,lty=2)
-
> lines(seq(-1,35,by=.2),P,lwd=2,col="red")
-
> P0=predict(r,type="response",se.fit=TRUE,
-
+ newdata=data.frame(speed=30))
-
> points(30,P1$fit,pch=4,lwd=3)
即

最大似然估计。
![]()
,Fisher信息来自标准最大似然理论。
![]()
这些值的计算基于以下计算
在对数泊松回归的情况下,
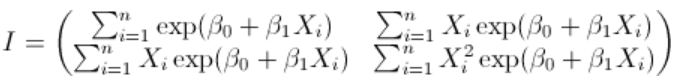
让我们回到最初的问题。
- 线性组合的置信区间
获得置信区间的第一个想法是获得置信区间(通过取边界的指数值)。渐近地,我们知道
![]()
因此,方差矩阵的近似将基于通过插入参数的估计量而获得。
然后,由于作为渐近多元分布,参数的任何线性组合也将是正态的,即具有正态分布。所有这些数量都可以轻松计算。首先,我们可以得到估计量的方差
因此,如果我们与回归的输出进行比较,
-
> summary(reg)$cov.unscaled
-
(Intercept) speed
-
(Intercept) 0.0066870446 -3.474479e-04
-
speed -0.0003474479 1.940302e-05
-
> V
-
[,1] [,2]
-
[1,] 0.0066871228 -3.474515e-04
-
[2,] -0.0003474515 1.940318e-05
根据这些值,很容易得出线性组合的标准偏差,
一旦我们有了标准偏差和正态性,就得出了置信区间,然后,取边界的指数,就得到了置信区间
-
> segments(30,exp(P2$fit-1.96*P2$se.fit),
-
+ 30,exp(P2$fit+1.96*P2$se.fit),col="blue",lwd=3)
基于该技术,置信区间不再以预测为中心。

- 增量法
实际上,使用表达式作为置信区间不会喜欢非中心区间。因此,一种替代方法是使用增量方法。我们可以使用一个程序包来计算该方法,而不是在理论上再次写一些东西,
-
-
-
-
-
> P1
-
$fit
-
1
-
155.4048
-
-
$se.fit
-
1
-
8.931232
-
-
$residual.scale
-
[1] 1
增量法使我们具有(渐近)正态性,因此一旦有了标准偏差,便可以得到置信区间。

通过两种不同的方法获得的数量在这里非常接近
-
> exp(P2$fit-1.96*P2$se.fit)
-
1
-
138.8495
-
> P1$fit-1.96*P1$se.fit
-
1
-
137.8996
-
> exp(P2$fit+1.96*P2$se.fit)
-
1
-
173.9341
-
> P1$fit+1.96*P1$se.fit
-
1
-
172.9101
- bootstrap技术
第三种方法是使用bootstrap技术基于渐近正态性(仅50个观测值)得出这些结果。我们的想法是从数据集中取样,并对这些新样本进行log-Poisson回归,并重复很多次数,
参考文献
2.R语言线性判别分析(LDA),二次判别分析(QDA)和正则判别分析(RDA)
5.在r语言中使用GAM(广义相加模型)进行电力负荷时间序列分析
6.使用SAS,Stata,HLM,R,SPSS和Mplus的分层线性模型HLM
▍关注我们
【大数据部落】第三方数据服务提供商,提供全面的统计分析与数据挖掘咨询服务,为客户定制个性化的数据解决方案与行业报告等。
▍咨询链接:http://y0.cn/teradat
▍联系邮箱:3025393450@qq.com


