拓端tecdat|R语言编程指导小数定律的保险业应用：泊松分布模拟索赔次数

 

原文链接：http://tecdat.cn/?p=14080

 

在保险业中，由于分散投资，通常会在合法的大型投资组合中提及大数定律。在一定时期内，损失“可预测”。当然，在标准的统计假设下，即有限的期望值和独立性。由于在保险业中，灾难通常很少发生，而且代价非常高昂，精算师可能有兴趣对少量事件的发生进行建模。背后的定理有时也被称为小数定律。

 

泊松分布

所谓的泊松分布（请参阅http://en.wikipedia.org/…）由SiméonPoisson于1837年进行了介绍。亚伯拉罕·德·莫伊夫（Abraham De Moivre）于1711年在De Mensura Sortis seu对其进行了定义。

让  表示一个计数随机变量，然后它是服从泊松分布，如果有  这样

De Moivre从二项式分布的近似值获得了该分布。回想一下，二项式分布是精算科学中的标准分布，例如，用来模拟被保险人死亡人数  。如果单个死亡概率相同，例如，并且如果死亡是独立事件，则

而如果  和  ，然后

再次，这是一个渐近定理，当我们有很多观察值时（）成立，它也成立，而且出现的可能性应该非常小（因为），这就是为什么要使用术语“ 小数”的原因。SiméonPoisson对数学近似值不感兴趣：他的主要观点是针对他正在处理的数据获得具有良好拟合优度的分布。

小数定律

与Poisson分布有关的主要定理的启发式如下：  表示iid随机变量采用值（一般情况下，一个分量可以是时间，另一分量可以是感兴趣的上部区域，其中某些随机过程是可能）。让。如果  作为假设（或更具体地假设），则  表示事件的（随机变量表征）计数，则  可以通过带有参数的泊松分布来近似。
启发式方法是，如果考虑大量观察值，并且计算给定（小）区域中有多少观察值，则此类观察值的数量就是泊松分布。

1.  
   n=1000
2.  
    
3.  
    
4.  
    
5.  
    
6.  
    
7.  
    
8.  
   polygon(c(u,rev(u)),c(v,rev(-v)),col="yellow",border=NA)
9.  
   I=(X^2+Y^2)<1
10.  
    points(X[I],Y[I],cex=.6,pch=19,col="red")

 

如果我们进行一些模拟

1.  
   > n=1000
2.  
   > ns=100000
3.  
   > N=rep(NA,ns)
4.  
   >
5.  
   +
6.  
   +
7.  
   +
8.  
   +
9.  
   +
10.  
    >
11.  
    > mean(N)
12.  
    [1] 31.41257

 

泊松分布的参数是黄色圆盘的面积，即正方形的面积，即

1.  
    
2.  
   > lines(0:60-.5,dpois(0:60,lambda),type="b",col="red")

 

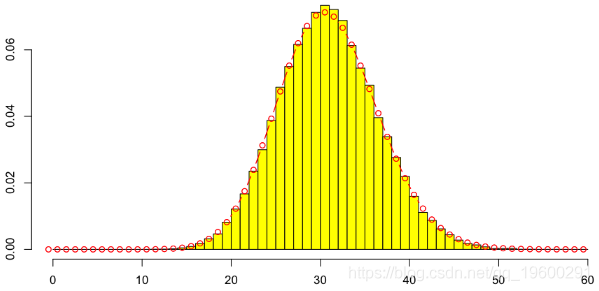
为了获得与保险模型有关的解释，让我们  在再保险合同中表示上层，即某些可扣除额。让我们  来表示个人损失。然后，可以使用泊松分布对到达该上层的索赔的数量进行建模。更准确地说，如果自付额  变得非常大（和），我们将获得极值理论中的阈值点以上模型：如果  有一个泊松分布，并在有条件的，  是独立同分布的广义帕累托随机变量，然后 具有广义的极值分布。因此，超出模型（针对罕见事件）与泊松过程密切相关。

泊松过程

如上所述，当事件以某种方式随机且独立地随时间发生时，就会出现泊松分布。然后很自然地研究两次事件之间的时间（或在保险范围内两次索赔）。

泊松分布和索赔发生

既不是SiméonPoisson也不是De Moivre，而是Ladislaus Von Bortkiewicz首先提到了Poisson分布是小数定律。1898年，他研究了1875年至1894年间被马踢倒杀死的士兵的人数，其中有200个兵团。

他确实获得了以下分布（此处，泊松分布的参数为0.61，即每年的平均死亡人数）

 

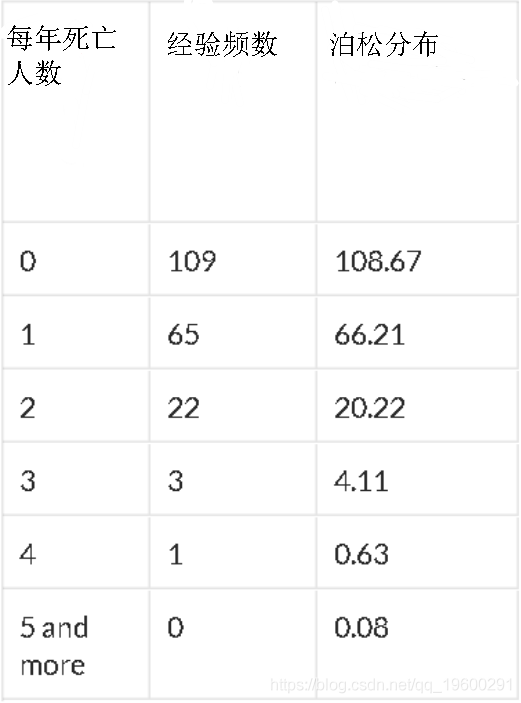
在很多情况下，泊松分布都非常适合。例如，如果我们考虑1850年后在佛罗里达州的飓风数量，

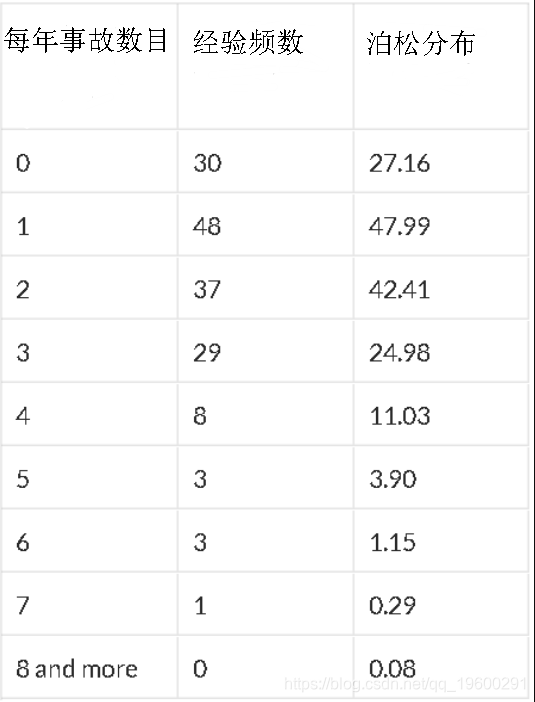
泊松分布和回归期

返回期是由Emil Gumbel在水文学中介绍的，用于链接概率和持续时间。十年事件的发生概率为1/10。那么10是发生之前的平均等待时间。这并不意味着该事件不会在10年之前发生，或者必须在10年之前发生。考虑一个返回期  （以年为单位），则每年不出现的概率为。

则多年未发生的概率为  。通常用下表来总结此属性，

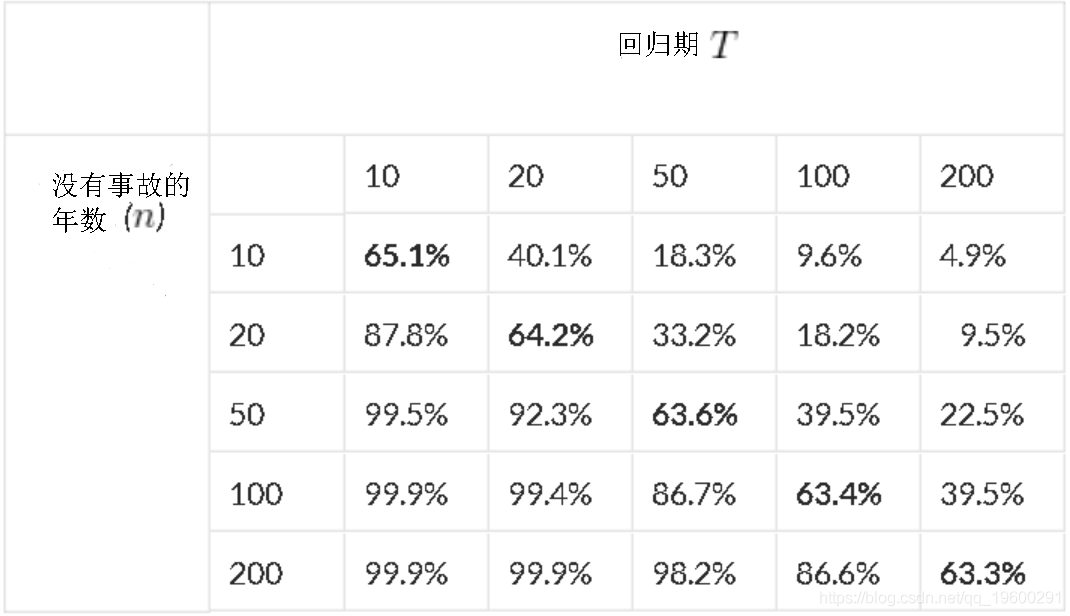
上表中的对角线非常有趣。似乎在某种程度上趋向极限值（此处为63.2％）。在n年内观察到的事件数量具有二项式分布，其概率为，将收敛到参数为1的泊松分布。那么，没有灾难的概率为，等于0.632。

稀有概率与泊松分布

计算稀有事件的概率时，泊松分布不断出现。例如，在50年的时间里，至少有一次在核电厂发生事故的可能性。假设在反应堆中发生事故的年概率  很小，例如0.05％。进一步假设反应堆在时间上相互独立。在50年内发生超过80个反应堆的事件的概率是

当然，线性近似是不正确的

另一方面

1.  
   >
2.  
   >
3.  
   [1] 0.1812733
4.  
   >
5.  
   [1] 0.1812692

 

这是具有参数为的泊松分布时为零  的概率  。我们在这里清楚地看到近似在风险管理中的应用。

解决这个问题的另一种方法是基于以下思想：鉴于在对全球450座反应堆进行的45年观察中（，观察到了三起重大事故，包括“三哩岛”（1979年）和“福岛”（2011年），即两次事故之间的平均时间估计为16年。对于单个反应堆，我们可以假设事件发生之前等待的平均时间是16年的450倍，即7200年。或者，一个反应堆在一年内发生一次事件的概率是7200以上的事件之一（这是“返还期”概念背后的想法）。如果我们假设事故的到来是随机且彼此独立发生的（如上定义），则在50年内观察到的重大事故数量遵循参数为50 /（7200/80）的泊松分布。也，

即

1.  
   >
2.  
   [1] 0.4262466

---

参考文献

1.R语言泊松Poisson回归模型分析案例

2.R语言进行数值模拟：模拟泊松回归模型

3.r语言泊松回归分析

4.R语言对布丰投针（蒲丰投针）实验进行模拟和动态可视化

5.用R语言模拟混合制排队随机服务排队系统

6.GARCH（1,1），MA以及历史模拟法的VaR比较

7.R语言做复杂金融产品的几何布朗运动的模拟

8.R语言进行数值模拟：模拟泊松回归模型

9.R语言对巨灾风险下的再保险合同定价研究案例：广义线性模型和帕累托分布Pareto distributions