拓端tecdat|R语言编程指导预测人口死亡率：用李·卡特模型、非线性模型进行平滑估计

原文链接：http://tecdat.cn/?p=13663

 

---

 

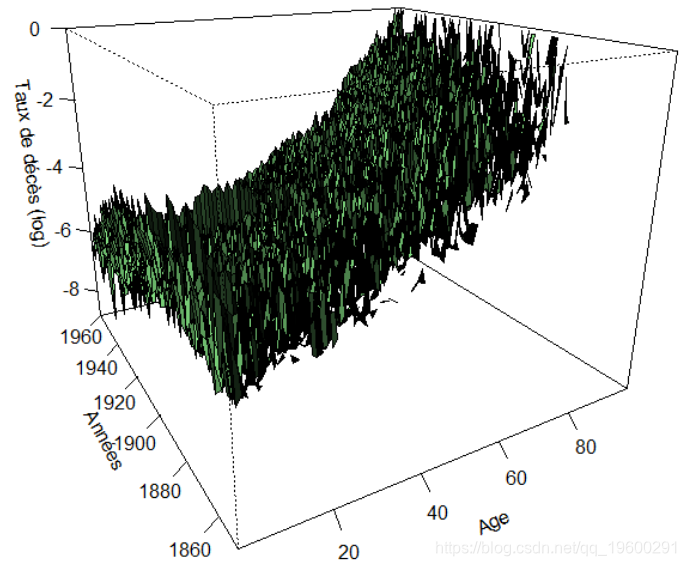
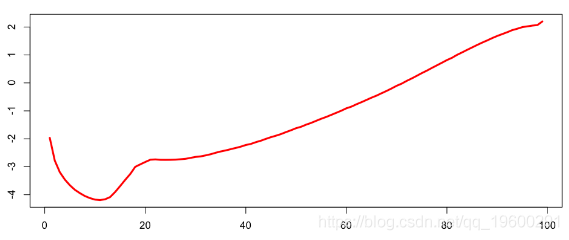
今天早上，我和同事一起分析死亡率。我们在研究人口数据集，可以观察到很多波动性。我们得到这样的结果：

​

 

由于我们缺少一些数据，因此我们想使用一些广义非线性模型。因此，让我们看看如何获​​得死亡率曲面图的平滑估计。我们编写一些代码。

D=DEATH$Male
E=EXPO$Male
A=as.numeric(as.character(DEATH$Age))
Y=DEATH$Year
I=(A<100)
base=data.frame(D=D,E=E,Y=Y,A=A)
subbase=base[I,]
subbase=subbase[!is.na(subbase$A),]

第一个想法可以是使用Poisson模型，其中死亡率是年龄和年份的平稳函数，类似于

​可以使用

persp(vZ,theta=-30,col="green",shade=TRUE,xlab="Ages (0-100)",
ylab="Years (1900-2005)",zlab="Mortality rate (log)")

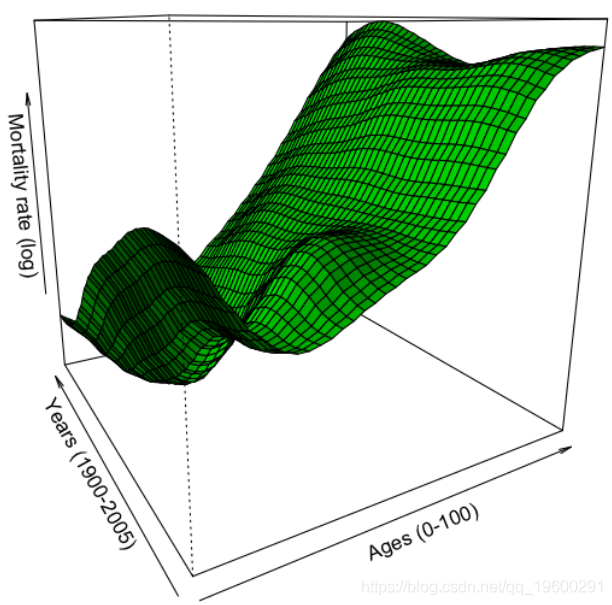
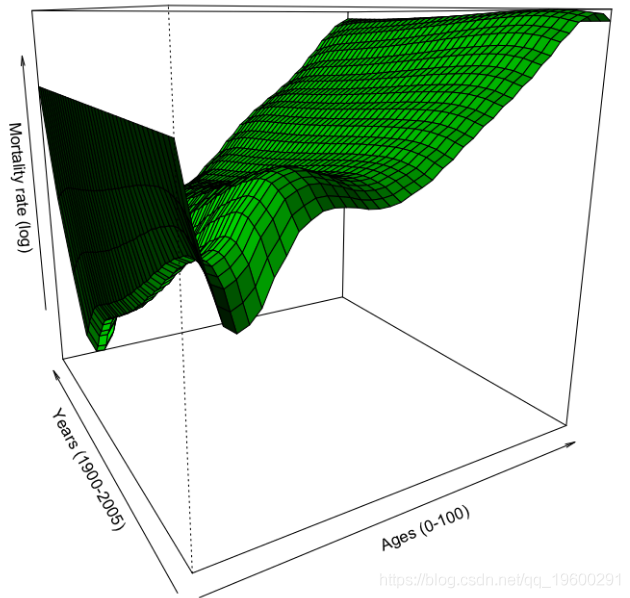
死亡率曲面图

​

 

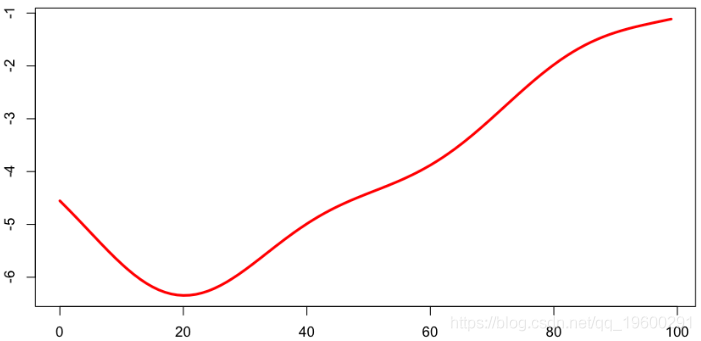
还可以提取年份的平均值，这是​ Lee-Carter模型中系数的解释  

predAx=function(a) mean(predict(regbsp,newdata=data.frame(A=a,
Y=seq(min(subbase$Y),max(subbase$Y)),E=1)))
plot(seq(0,99),Vectorize(predAx)(seq(0,99)),col="red",lwd=3,type="l")

我们有以下平滑的死亡率

​

 

回顾下李·卡特模型是

​

可以使用以下方法获得参数估计值

persp(vZ,theta=-30,col="green",shade=TRUE,xlab="Ages (0-100)",
ylab="Years (1900-2005)",zlab="Mortality rate (log)")

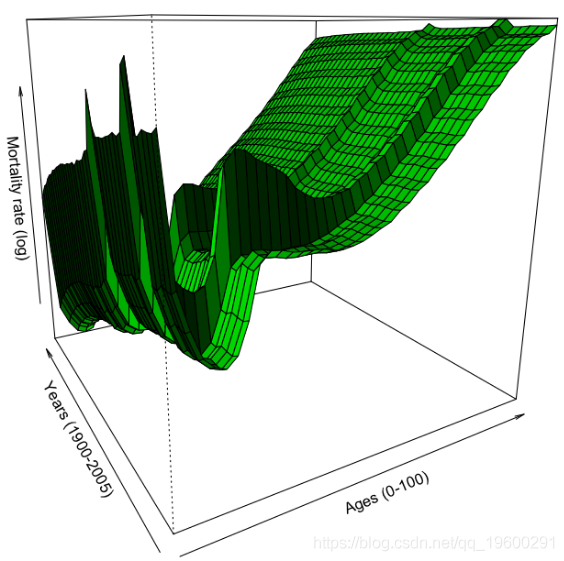
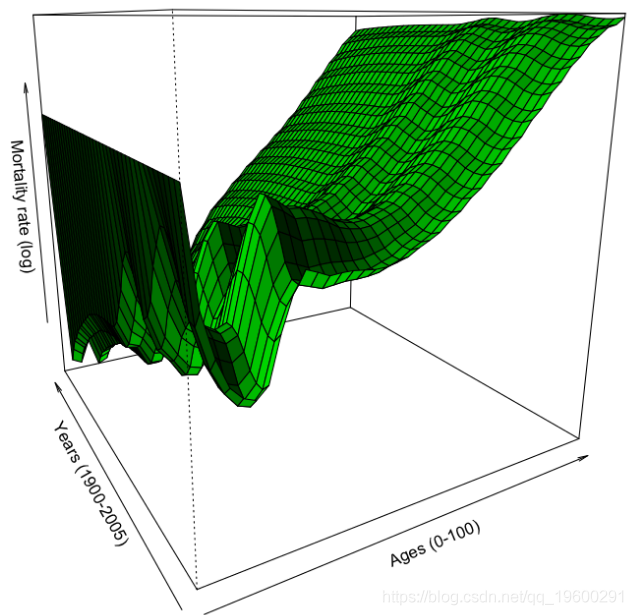
粗略的死亡率曲面图是

​

 

有以下  ​ 系数。

plot(seq(1,99),coefficients(regnp)[2:100],col="red",lwd=3,type="l")

​

 

这里我们有很多系数，但是，在较小的数据集上，我们具有更多的可变性。我们可以平滑李·卡特模型： 

​

 代码片段

persp(vZ,theta=-30,col="green",shade=TRUE,xlab="Ages (0-100)", 
ylab="Years (1900-2005)",zlab="Mortality rate (log)")

现在的死亡人数是

​

 

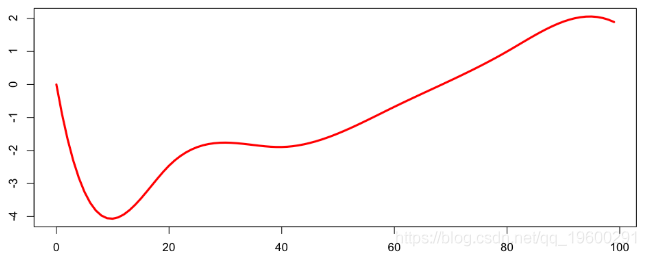
得出多年来随年龄变化的平均死亡率，

BpA=bs(seq(0,99),knots=knotsA,Boundary.knots=range(subbase$A),degre=3)
Ax=BpA%*%coefficients(regsp)[2:8]
plot(seq(0,99),Ax,col="red",lwd=3,type="l")

​

 

然后，我们可以使用样条函数的平滑参数，并查看对死亡率曲面的影响

persp(vZ,theta=-30,col="green",shade=TRUE,xlab="Ages (0-100)",
ylab="Years (1900-2005)",zlab="Mortality rate (log)")

​