拓端tecdat|R语言编程指导对混合分布中的不可观测与可观测异质性因子分析

原文链接：http://tecdat.cn/?p=13584 

---

今天上午，在课程中，我们讨论了利率制定中可观察和不可观察异质性之间的区别（从经济角度出发）。为了说明这一点，我们看了以下简单示例。让  X 代表一个人的身高。考虑以下数据集

> Davis[12,c(2,3)]=Davis[12,c(3,2)] 

 在这里，关注变量是给定人的身高，

> X=Davis$height 

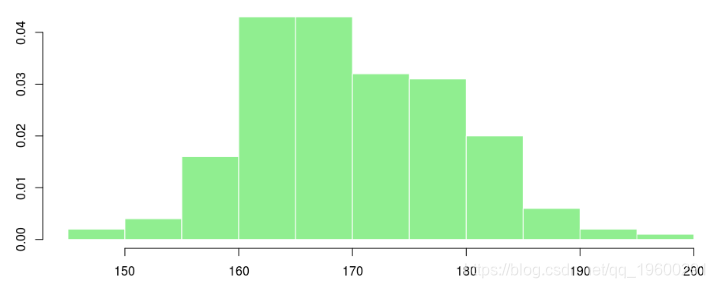
如果我们看直方图，我们有

> hist(X,col="light green", border="white",proba=TRUE,xlab="",main="")

​

我们可以假设我们具有高斯分布吗？

​

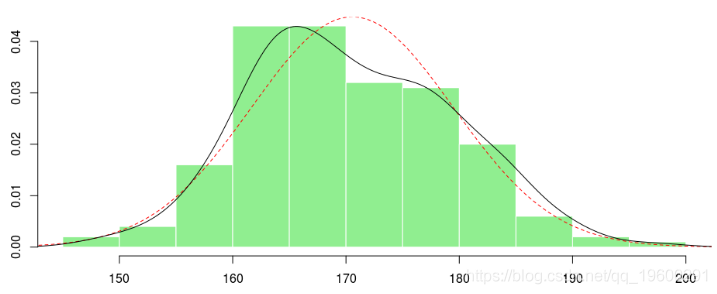
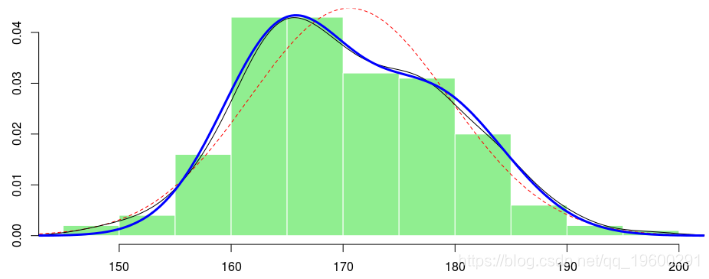
在这里，如果我们拟合高斯分布，将其绘制出来，并添加基于核的估计量，我们将得到

> (param <- fitdistr(X,"normal")$estimate) 
> f1 <- function(x) dnorm(x,param[1],param[2]) 
> x=seq(100,210,by=.2) 
> lines(x,f1(x),lty=2,col="red") 
> lines(density(X))

​

 

 

如果看那条黑线，可能会想到一种混合分布，例如

​

当我们有一个获得混合分布不可观察的异质性因子：概率 p1，一个随机变量  ​ ，概率p2，一个随机变量  ​ 。我们可以使用例如

> (param12 <- c(mix$lambda[1],mix$mu,mix$sigma)) 
[1] 0.4002202 178.4997298 165.2703616 6.3561363 5.9460023  

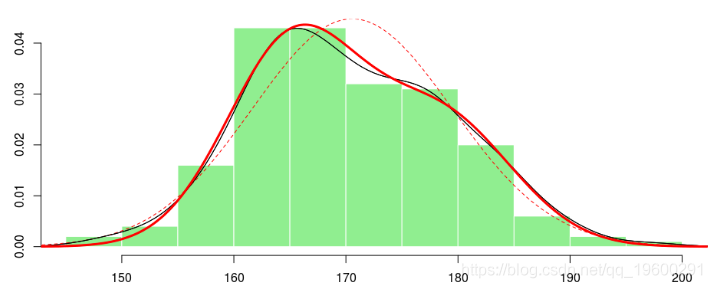
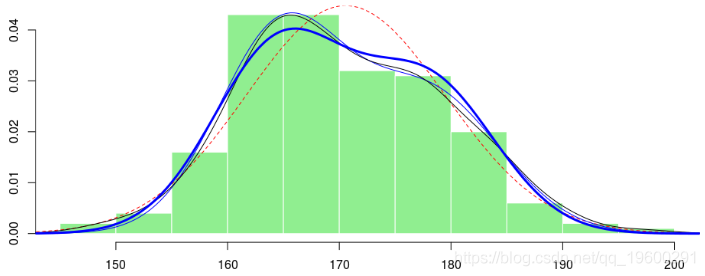
 如果我们绘制两个高斯分布的混合图，我们得到

> lines(x,f2(x),lwd=2, col="red") lines(density(X))

​

不错。实际上，我们可以尝试使用自己的代码最大限度地提高可能性，

> bvec <- c(0,-1,0,0)
> constrOptim(c(.5,160,180,10,10), logL, NULL, ui = Amat, ci = bvec)$par

[1]   0.5996263 165.2690084 178.4991624   5.9447675   6.3564746

在这里，我们包括一些约束，以保证概率属于单位间隔，并且方差参数保持正值。

进一步来说，如果我们假设基础分布具有相同的方差，即

​

在这种情况下，我们必须使用之前的代码，并进行一些小的更改，

> (param12c= constrOptim(c(.5,160,180,10), logL, NULL, ui = Amat, ci = bvec)$par)

[1]   0.6319105 165.6142824 179.0623954   6.1072614

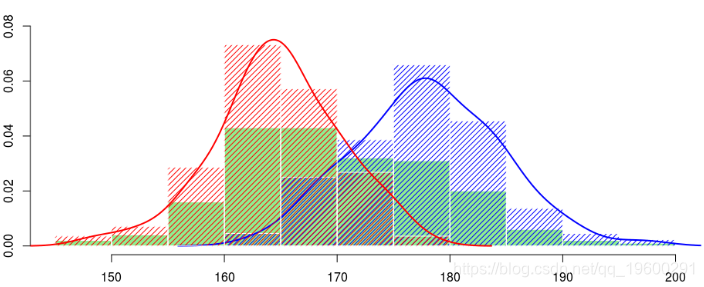
如果我们不能观察到异质性因素，这就是我们可以做的。我们实际上在数据集中有一些信息。例如，我们具有人的性别。现在，如果我们查看每个性别的身高直方图，以及基于内核的每个性别的身高密度估计量，

​

 

因此，看起来男性的身高和女性的身高是不同的。也许我们可以使用实际观察到的变量来解释样本中的异质性。在形式上，这里的想法是考虑具有可观察到的异质性因素的混合分布：性别，

​

现在，我们对以前称为类[1]和[2]的解释是：男性和女性。在这里，估算参数非常简单，

sex=="F"
      mean         sd 
164.714286   5.633808 
sex=="M"
      mean         sd 
178.011364   6.404001

如果我们绘制密度，我们有

> lines(x,f4(x),lwd=3,col="blue")

​

 

如果再次假设相同的方差怎么办？即，模型变为

​然后，一个自然的想法是根据以前的计算得出方差的估计量

​

 

> s
[1] 6.015068

再一次，可以绘制相关的密度，

> lines(x,f5(x),lwd=3,col="blue")

​

现在，如果我们仔细考虑一下我们所做的事情，那仅仅是对一个因素（人的性别）的线性回归，

​

  ​

实际上，如果我们运行代码来估算此线性模型，

Residuals:
     Min       1Q   Median       3Q      Max 
-16.7143  -3.7143  -0.0114   4.2857  18.9886 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 164.7143     0.5684  289.80   <2e-16 ***
sexM         13.2971     0.8569   15.52   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.015 on 198 degrees of freedom
Multiple R-squared:  0.5488,	Adjusted R-squared:  0.5465 
F-statistic: 240.8 on 1 and 198 DF,  p-value: < 2.2e-16

我们得到的均值和方差的估计与之前获得的估计相同。因此，正如今天上午在课堂上提到的，如果您有一个不可观察的异质性因子，我们可以使用混合模型来拟合分布，但是如果您可以得到该因子的替代，这是可观察的，则可以运行回归。