拓端tecdat|R语言编程指导基于混合数据抽样(MIDAS)回归的HAR-RV模型预测GDP增长
原文链接:http://tecdat.cn/?p=12292
预测GDP增长
我们复制了Ghysels(2013)中提供的示例。我们进行了MIDAS回归分析,以预测季度GDP增长以及每月非农就业人数的增长。预测公式如下
其中yt是按季度季节性调整后的实际美国GDP的对数增长,x3t是月度总就业非农业工资的对数增长。
首先,我们加载数据并执行必要的转换。
最后两行用于均衡样本大小,样本大小在原始数据中有所不同。我们只需在数据的开头和结尾添加其他NA值即可。数据的图形表示如图3所示。要指定midas_r函数的模型,我们以下等效形式重写它:
就像在Ghysels(2013)中一样,我们将估算样本限制在1985年第一季度到2009年第一季度之间。我们使用Beta多项式,非零Beta和U-MIDAS权重规格来评估模型。
我们可以使用2009年第2季度至2011年第2季度包含9个季度的样本数据评估这三个模型的预测性能。
我们看到,MIDAS回归模型提供了最佳的样本外RMSE。
预测实际波动
作为另一个演示,我们使用midasr来预测每日实现的波动率。Corsi(2009)提出了一个简单的预测每日实际波动率的模型。实现波动率的异质自回归模型(HAR-RV)定义为
我们假设一周有5天,一个月有4周。该模型是MIDAS回归的特例:
相应的R代码如下
为了进行经验论证,我们使用了由Heber,Lunde,Shephard和Sheppard(2009)提供的关于股票指数的已实现波动数据。我们基于5分钟的回报数据估算S&P500指数的年度实现波动率模型。
为了进行比较,我们还使用归一化指数Almon权重来估计模型
我们可以使用异方差性和自相关鲁棒权重规范测试hAhr_test来测试这些限制中哪些与数据兼容。
我们可以看到,与MIDAS回归模型中的HAR-RV隐含约束有关的零假设在0.05的显着性水平上被拒绝,而指数Almon滞后约束足够的零假设则不能被拒绝。
图说明了拟合的MIDAS回归系数和U-MIDAS回归系数及其相应的95%置信区间。对于指数Almon滞后指标,我们可以通过AIC或BIC选择滞后次数。
在这里,我们使用了两种优化方法来提高收敛性。将测试函数应用于每个候选模型。函数hAhr_test需要大量的计算时间,尤其是对于滞后数量较大的模型,因此我们仅在第二步进行计算,并且限制了滞后次数的选择。AIC选择模型有9个滞后:
hAh_test的HAC再次不拒绝指数Almon滞后规范的原假设。我们可以使用具有1000个观测值窗口的滚动预测来研究两个模型的预测性能。为了进行比较,我们还计算了无限制AR(20)模型的预测。
我们看到指数Almon滞后模型略胜于HAR-RV模型,并且两个模型均胜过AR(20)模型。
参考文献
Andreou E,Ghysels E,Kourtellos A(2010)。“具有混合采样频率的回归模型。” 计量经济学杂志,158,246–261。doi:10.1016 / j.jeconom.2010.01。004。
Andreou E,Ghysels E,Kourtellos A(2011)。“混合频率数据的预测。” 在MP Clements中,DF Hendry(编),《牛津经济预测手册》,第225–245页。


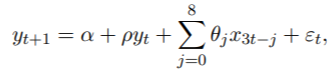
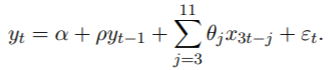

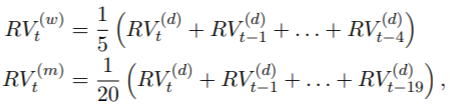
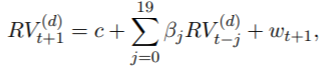
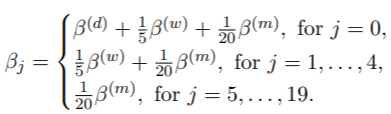


 浙公网安备 33010602011771号
浙公网安备 33010602011771号