拓端tecdat|R语言编程指导中的马尔科夫机制转换(Markov regime switching)模型

原文链接：http://tecdat.cn/?p=12187

---

 

金融分析师通常关心检测市场何时“发生变化”：几个月或至几年内市场的典型行为可以立即转变为非常不同的行为。投资者希望及时发现这些变化，以便可以相应地调整其策略，但是这样做可能很困难。

RHmm从CRAN不再可用，因此我想使用其他软件包复制功能实现马尔科夫机制转换(Markov regime switching)模型从而对典型的市场行为进行预测，并且增加模型中对参数的线性约束功能。

 

library(SIT)
load.packages('quantmod')

	# find regimes
	load.packages('RHmm', repos ='http://R-Forge.R-project.org')

	y=returns
	ResFit = HMMFit(y, nStates=2)
	VitPath = viterbi(ResFit, y)

DimObs = 1

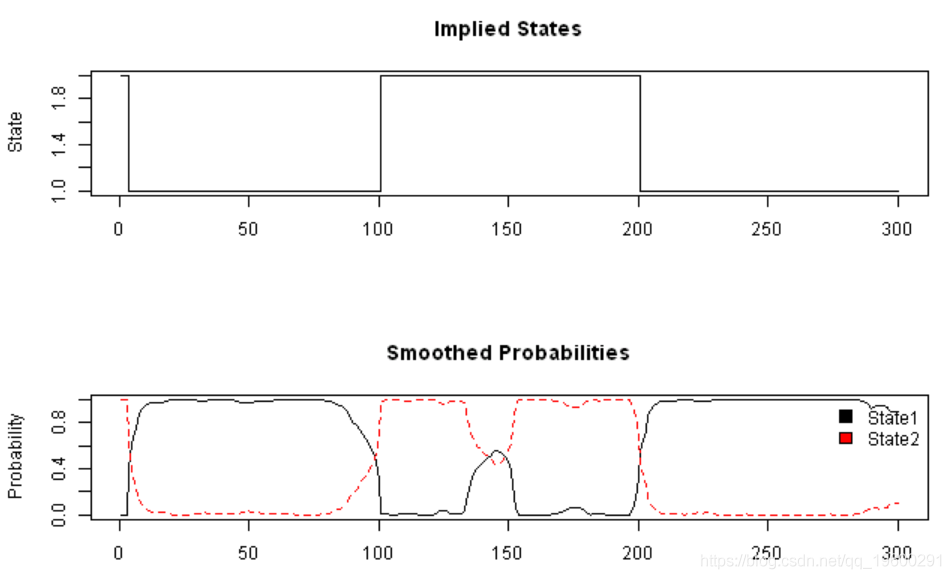
	matplot(fb$Gamma, type='l', main='Smoothed Probabilities', ylab='Probability')
		legend(x='topright', c('State1','State2'),  fill=1:2, bty='n')

 

​

 

	fm2 = fit(mod, verbose = FALSE)

使用logLik在迭代69处收敛：125.6168

 

	probs = posterior(fm2)

	layout(1:2)
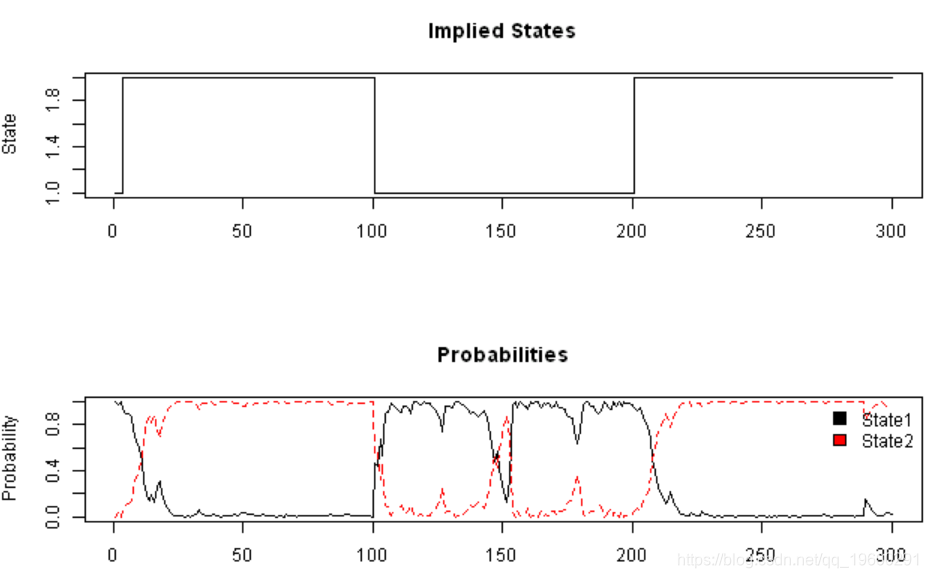
	plot(probs$state, type='s', main='Implied States', xlab='', ylab='State')
	
	matplot(probs[,-1], type='l', main='Probabilities', ylab='Probability')
		legend(x='topright', c('State1','State2'),  fill=1:2, bty='n')

​

 

	#*****************************************************************
	# Add some data and see if the model is able to identify the regimes
	#****************************************************************** 
	bear2  = rnorm( 100, -0.01, 0.20 )
	bull3 = rnorm( 100, 0.10, 0.10 )
	bear3  = rnorm( 100, -0.01, 0.25 )
	true.states = c(true.states, rep(2,100),rep(1,100),rep(2,100))
	y = c( bull1, bear,  bull2, bear2, bull3, bear3 )

DimObs = 1

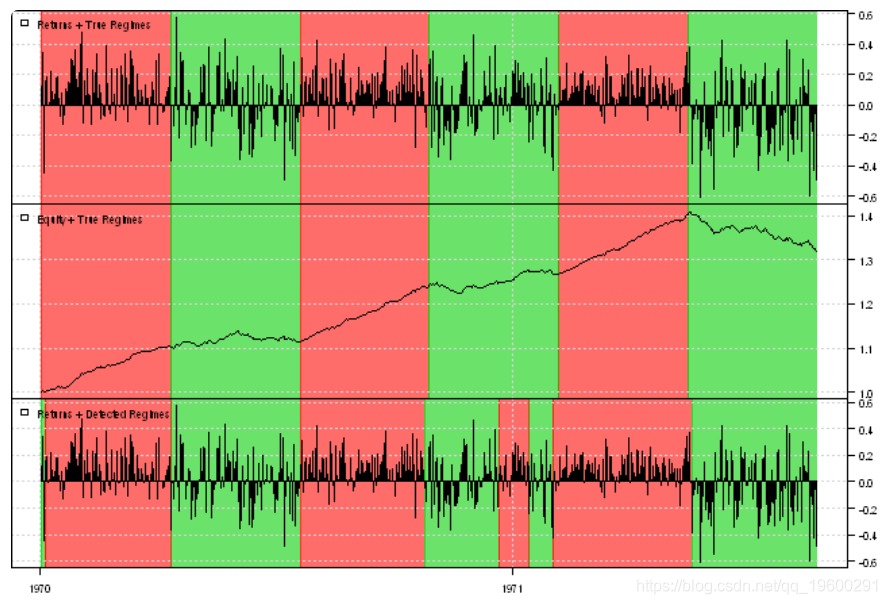
	plota(data, type='h', x.highlight=T)
		plota.legend('Returns + Detected Regimes')

​

 

#*****************************************************************
# Load historical prices
#****************************************************************** 
data = env()
getSymbols('SPY', src = 'yahoo', from = '1970-01-01', env = data, auto.assign = T)

price = Cl(data$SPY)
	open = Op(data$SPY)
ret = diff(log(price))
	ret = log(price) - log(open)

atr = ATR(HLC(data$SPY))[,'atr']

fm2 = fit(mod, verbose = FALSE)

使用logLik在迭代30处收敛：18358.98

print(summary(fm2))

 

Initial state probabilties model pr1 pr2 pr3 pr4 0 0 1 0

Transition matrix toS1 toS2 toS3 toS4 fromS1 9.821940e-01 1.629595e-02 1.510069e-03 8.514403e-45 fromS2 1.167011e-02 9.790209e-01 8.775478e-68 9.308946e-03 fromS3 3.266616e-03 8.586650e-47 9.967334e-01 1.350529e-69 fromS4 3.608394e-65 1.047516e-02 1.922545e-130 9.895248e-01

Response parameters Resp 1 : gaussian Resp 2 : gaussian Re1.(Intercept) Re1.sd Re2.(Intercept) Re2.sd St1 2.897594e-04 0.006285514 1.1647547 0.1181514 St2 -6.980187e-05 0.008186433 1.6554049 0.1871963 St3 2.134584e-04 0.005694483 0.4537498 0.1564576 St4 -4.459161e-04 0.015419207 2.7558362 0.7297283

 	Re1.(Intercept)	Re1.sd	Re2.(Intercept)	Re2.sd
St1	0.000289759401378951	0.00628551404616354	1.16475474419891	0.118151350440916
St2	-6.98018749098021e-05	0.00818643307634358	1.65540488736983	0.187196307284941
St3	0.000213458358141314	0.00569448330115608	0.453749781945066	0.156457606460757
St4	-0.00044591612667264	0.0154192070819596	2.75583620018895	0.72972830143278

 

probs = posterior(fm2)

print(head(probs))

rownames(x)	state	S1	S2	S3	S4
1	3	0	0	1	0
2	3	0	0	1	0
3	3	0	0	1	0
4	3	0	0	1	0
5	3	0	0	1	0
6	3	0	0	1	0

 

 

layout(1:3)
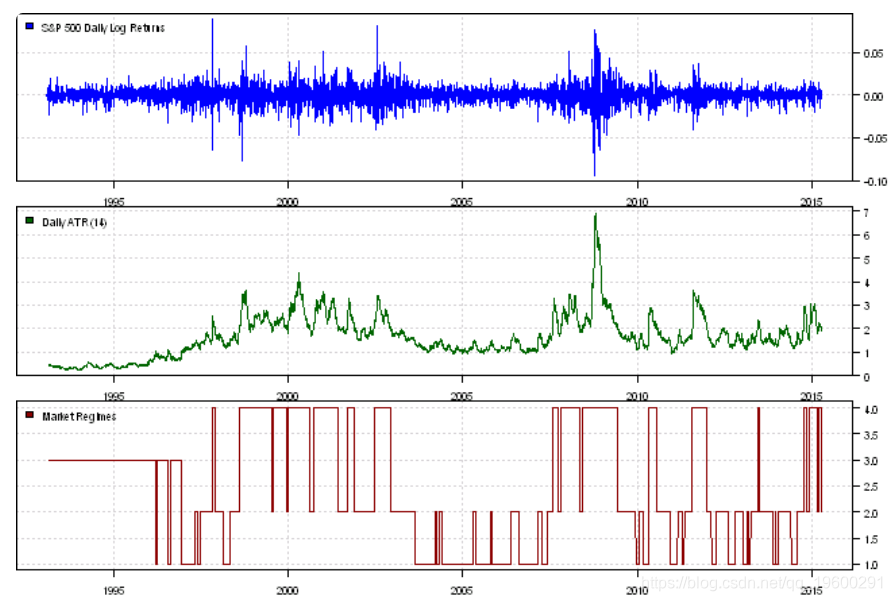
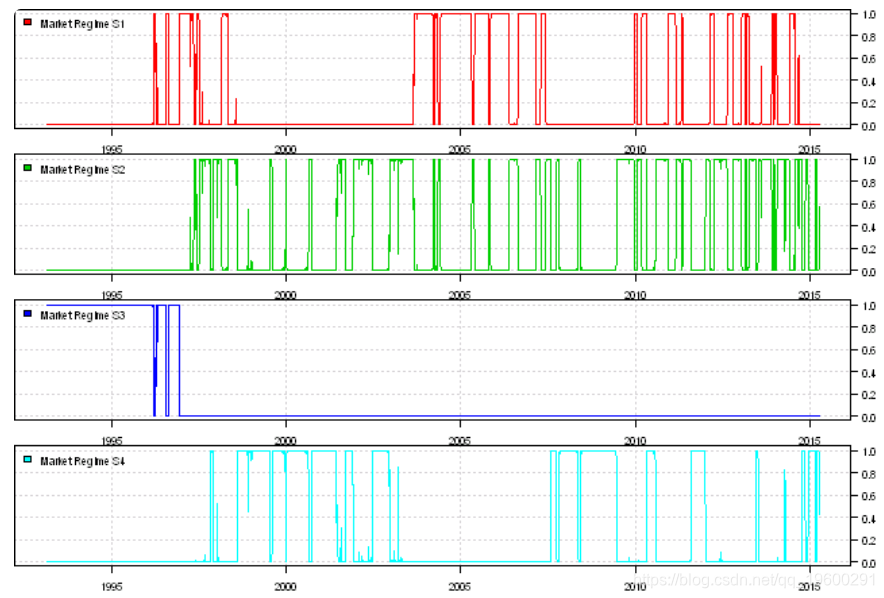
plota(temp, type='l', col='darkred')
	plota.legend('Market Regimes', 'darkred')

​

 

layout(1:4)

​