拓端tecdat|matlab编程代写中的隐马尔可夫模型(HMM)实现
原文链接：http://tecdat.cn/?p=7960
隐马尔可夫模型（HMM）简介
隐马尔可夫模型（HMM）是一个在你观察到的输出顺序，但不知道状态序列模型产生输出的过程。隐马尔可夫模型的分析试图从观察到的数据中恢复状态序列。
例如，考虑具有两个状态和六个可能输出的马尔可夫模型。该模型使用：
-
红色骰子，有六个面，标记为1到6。
-
一个绿色骰子，具有十二个侧面，其中五个侧面标记为2到6，其余七个侧面标记为1。
-
加权的红色硬币，正面出现概率为.9，背面出现概率为1.。
-
加权绿色硬币，其正面概率为0.95，背面概率为.05。
该模型使用以下规则从集合{1、2、3、4、5、6}中创建数字序列：
-
首先滚动红色骰子，然后写下出现的数字 。
-
投掷红色硬币并执行以下操作之一：
-
如果结果为正面，则滚动红色骰子并记下结果。
-
如果结果是反面，则滚动绿色骰子并记下结果。
-
-
在随后的每个步骤中，您翻转与上一步中滚动的骰子颜色相同的颜色的硬币。如果硬币正面朝上，则与上一步骤滚动相同的骰子。如果硬币出现反面，请切换到另一个骰子。
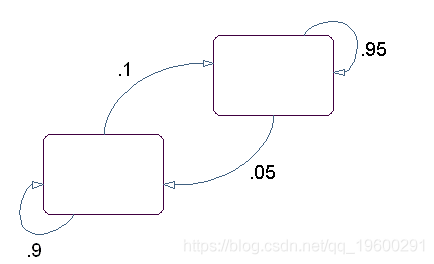
该模型的状态图具有红色和绿色两种状态，如下图所示。
您可以通过滚动具有与状态相同颜色的骰子来确定状态的发射。您可以通过翻转与状态相同颜色的硬币来确定到下一个状态的过渡。
转换矩阵为：
T = [0.90.050.10.95]
输出矩阵为：
该模型不是隐藏的，因为您可以从硬币和骰子的颜色知道状态的顺序。但是，假设其他人 没有向您显示骰子或硬币。您所看到的只是输出的顺序。如果开始看到的数字比其他数字多1，则可能会怀疑骰子处于绿色状态，但由于无法看到要滚动的骰子的颜色，因此无法确定。
隐藏的马尔可夫模型提出以下问题：
-
给定一系列输出，最可能的状态路径是什么？
-
给定一系列输出，您如何估算模型的转换和输出概率？
-
什么是后验概率？
分析隐马尔可夫模型
本节说明如何来分析隐马尔可夫模型。
生成测试序列
TRANS = [.9 .1; .05 .95];
EMIS = [1/6, 1/6, 1/6, 1/6, 1/6, 1/6;...
7/12, 1/12, 1/12, 1/12, 1/12, 1/12];要从模型生成状态和发射的随机序列 ：
输出seq是序列，输出states是状态序列。
估计状态序列
likelystates是与长度相同的序列seq。
要测试的准确性hmmviterbi 。
sum(states==likelystates)/1000
ans =
0.8200在这种情况下，最有可能的状态序列在82％的时间内与随机序列一致。
估算转移和输出矩阵
返回转换矩阵和输出矩阵的估计值：
您可以将输出与原始 矩阵进行比较， TRANS并且EMIS：
TRANS
TRANS =
0.9000 0.1000
0.0500 0.9500
EMIS
EMIS =
0.1667 0.1667 0.1667 0.1667 0.1667 0.1667
0.5833 0.0833 0.0833 0.0833 0.0833 0.0833
假设您对TRANS和 有以下初步猜测EMIS。
TRANS_GUESS = [.85 .15; .1 .9];
EMIS_GUESS = [.17 .16 .17 .16 .17 .17;.6 .08 .08 .08 .08 08];您估计TRANS并EMIS如下：
TRANS_EST2 =
0.2286 0.7714
0.0032 0.9968
EMIS_EST2 =
0.1436 0.2348 0.1837 0.1963 0.2350 0.0066
0.4355 0.1089 0.1144 0.1082 0.1109 0.1220 如果算法在最大迭代次数（默认值为）内未能达到此容差100，则算法将暂停。
如果算法未能达到所需的容差，请使用以下命令增加最大迭代次数的默认值：
其中，maxiter是算法执行的最大步骤数。
估计后验状态概率
输出PSTATES为M × L矩阵，其中M为状态数，L为的长度seq。PSTATES(i,j)是条件概率，该模型处于状态i时，它产生j的 seq给出的是，seq 。
要返回序列概率的对数seq，请使用第二个输出参数hmmdecode：
随着序列长度的增加，序列的概率趋于0 。
更改初始状态分布
默认情况下， 隐藏的Markov模型函数从状态1开始。换句话说，初始状态的分布将其所有概率质量都集中在状态1处。要分配不同的概率分布，p = [ p 1，p 2，...，p M ]，到M个初始状态，执行以下操作：
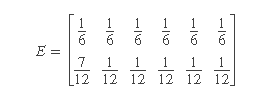
如果转换矩阵和发射矩阵分别为TRANS和EMIS，则可以使用以下命令来创建增强矩阵：
