拓端tecdat|R语言编程代写最优聚类数目k改进kmean聚类算法
原文链接：http://tecdat.cn/?p=7237
在本文中，我们将探讨应用聚类算法（例如k均值和期望最大化）来确定集群的最佳数量时所遇到的问题之一。从数据集本身来看，确定集群数量的最佳值的问题通常不是很清楚。在本文中，我们将介绍几种技术，可用于帮助确定给定数据集的最佳k值。
我们将在当前的R Studio环境中下载数据集：
StudentKnowledgeData <-read_csv（“ YourdownloadFolderPath / StudentKnowledgeData.csv”）
预处理
由于此数据集的特征向量较低，因此我们将不关注特征选择方面，而是将使用所有可用特征。
summary(myDataClean)
[1] 402 5
STG SCG STR LPR
Min. :0.0000 Min. :0.0000 Min. :0.0100 Min. :0.0000
1st Qu.:0.2000 1st Qu.:0.2000 1st Qu.:0.2700 1st Qu.:0.2500
Median :0.3025 Median :0.3000 Median :0.4450 Median :0.3300
Mean :0.3540 Mean :0.3568 Mean :0.4588 Mean :0.4324
3rd Qu.:0.4800 3rd Qu.:0.5100 3rd Qu.:0.6800 3rd Qu.:0.6500
Max. :0.9900 Max. :0.9000 Max. :0.9500 Max. :0.9900一旦完成预处理，以确保数据已准备就绪，可用于进一步的应用。
scaled_data = as.matrix（scale（myDataClean））
聚类算法– k表示在其中找到最佳聚类数的示例
让我们尝试为该数据创建聚类。
让我们从k = 3开始并检查结果。
kmm
K-means clustering with 3 clusters of sizes 93, 167, 142
Cluster means:
STG SCG STR LPR PEG
1 0.573053974 0.3863411 0.2689915 1.3028712 0.1560779
2 -0.315847301 -0.4009366 -0.3931942 -0.1794893 -0.8332218
3 -0.003855777 0.2184978 0.2862481 -0.6421993 0.8776957
Clustering vector:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
...................................................................................
Within cluster sum of squares by cluster:
[1] 394.5076 524.4177 497.7787
(between_SS / total_SS = 29.3 %)
Available components:
[1] "cluster" "centers" "totss" "withinss" "tot.withinss"
[6] "betweenss" "size" "iter" "ifault" 当我们检查（between_SS / total_SS）时，发现它很低。该比率实际上说明了群集之间数据点的平方总和。我们想要增加此值，并且随着群集数量的增加，我们看到它增加，但是我们不想过度拟合数据。因此，我们看到在k = 401的情况下，我们将拥有402个完全适合数据的簇。因此，我们的想法是找到一个k值，对于该值，模型不会过拟合，并且同时根据实际分布对数据进行聚类。现在让我们探讨如何解决找到最佳数目的群集的问题。
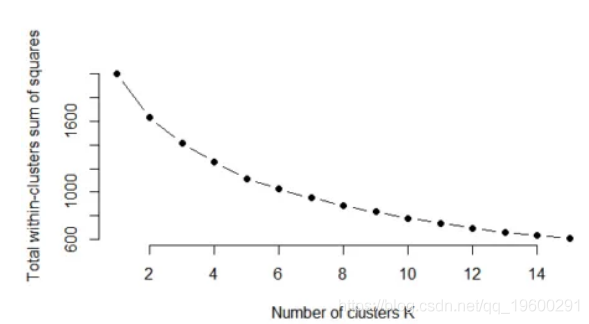
肘法
如果将集群解释的方差百分比相对于集群数量作图，则第一个集群会添加很多信息（说明很多方差），但在某个点上边际增益会下降，从而在图形。此时选择簇的数量，因此选择“肘部标准”。
wss
plot(1:k.max, wss,
type="b", pch = 19, frame = FALSE,
xlab="Number of clusters K",
ylab="Total within-clusters sum of squares")
[1] 2005.0000 1635.8573 1416.7041 1253.9959 1115.4657 1026.0506 952.4835 887.7202
[9] 830.8277 780.2121 735.6714 693.7745 657.0939 631.5901 608.3576该图可以在下面看到：
因此，对于k = 4，与其他k相比，between_ss / total_ss比率趋于缓慢变化且变化较小。因此对于该数据，k = 4应该是群集数量的一个不错的选择，
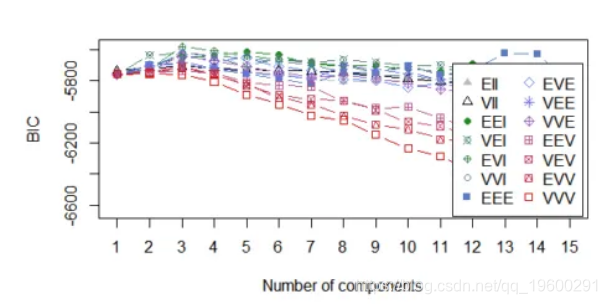
k均值的贝叶斯推断标准
k均值模型“几乎”是高斯混合模型，因此可以构造高斯混合模型的似然性，从而确定信息标准值。
d_clust$BIC
plot(d_clust)
Bayesian Information Criterion (BIC):
EII VII EEI VEI EVI VVI EEE EVE
1 -5735.105 -5735.105 -5759.091 -5759.091 -5759.091 -5759.091 -5758.712 -5758.712
2 -5731.019 -5719.188 -5702.988 -5635.324 -5725.379 -5729.256 -5698.095 -5707.733
3 -5726.577 -5707.840 -5648.033 -5618.274 -5580.305 -5620.816 -5693.977 -5632.555
..................................................................................
VEE VVE EEV VEV EVV VVV
1 -5758.712 -5758.712 -5758.712 -5758.712 -5758.712 -5758.712
2 -5704.051 -5735.383 -5742.110 -5743.216 -5752.709 -5753.597
3 -5682.312 -5642.217 -5736.306 -5703.742 -5717.796 -5760.915
..............................................................
Top 3 models based on the BIC criterion:
EVI,3 EVI,4 EEI,5
-5580.305 -5607.980 -5613.077
> plot(d_clust)
Model-based clustering plots:
1: BIC
2: classification
3: uncertainty
4: density
Selection: 1可以在下面看到该图，其中k = 3和k = 4是可用的最佳选择。
从这两种方法可以看出，我们可以在一定程度上确定对于聚类问题而言，聚类数的最佳值是多少。几乎没有其他技术可以使用。
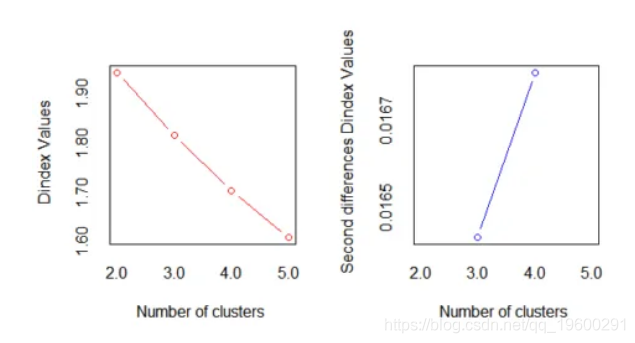
hist(nb$Best.nc[1,], breaks = max(na.omit(nb$Best.nc[1,])))在此有一个重要的要点，即对于每个群集大小，此方法始终考虑大多数索引。因此，重要的是要了解哪些索引与数据相关，并根据该索引确定最佳选择是建议的最大值还是任何其他值。
正如我们在下面查看“第二差分D-index”图所看到的，很明显，最佳聚类数是k = 4。
