拓端tecdat|R语言辅导rjags使用随机效应进行臭氧数据分析

原文链接：http://tecdat.cn/?p=6894

 

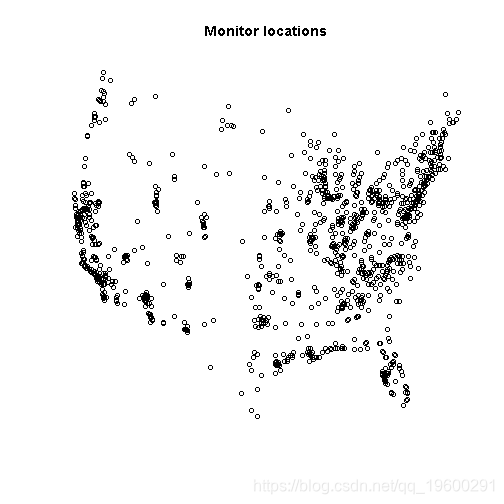
加载和格式化数据

rm(list=ls())
 ls()
## [1] "s" "Y"
dim(Y)
## [1] 1106   31
dim(s)
## [1] 1106    2
ns   <- nrow(Y)
  
plot(s,axes=FALSE,xlab="",ylab="",main="Monitor locations")

​

 abline(75,0,col=2)

​

 abline(75,0,col=2)

​

在JAGS中指定模型

Ozone_model <- "model{

   # Likelihood
 

   # Random effects
   for(i in 1:ns){
    alpha i] ~ dnorm(0, )
   }
   for(j in 1:nt){
    gamma j] ~ dnorm(0, )
   }

   # Priors
   mu   ~ dnorm(0,0.01)
 

   # Output the parameters of interest
   sigma2[1] <- 1/taue
 ] 
   pct[1]    <- sigma2[1]/sum(sigma2[])   
   pct[2]    <- sigma2[2]/sum(sigma2[])   
   pct[3]    <- sigma2[3]/sum(sigma2[])   

  }"


模型


dat    <- list(Y=Y,ns=ns,nt=nt)
model1 <- jags.model(textConnection(Ozone_model),inits=init,data = dat, n.chains=1)
## Compiling model graph
##    Resolving undeclared variables
##    Allocating nodes
##    Graph Size: 69733
## 
## Initializing model

​ ​ ​ ​ ​ ​ ​ ​ ​ ​

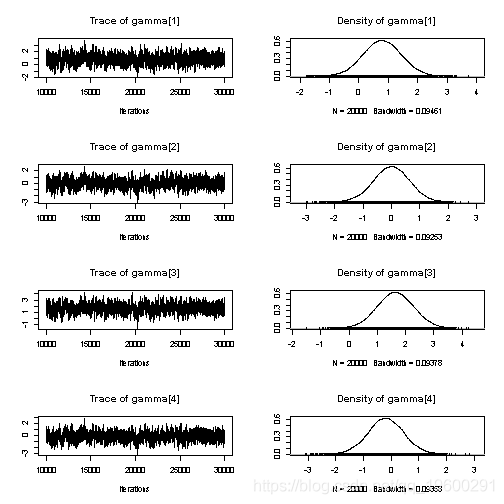
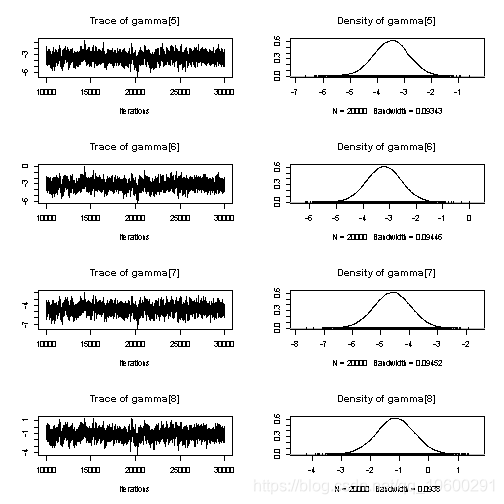
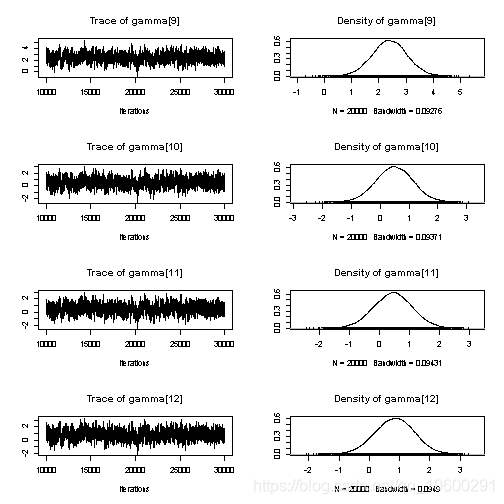
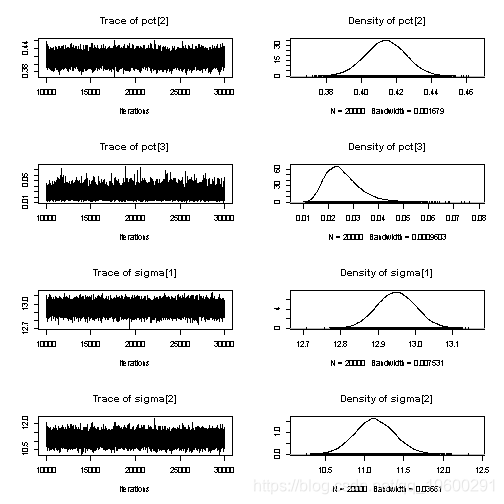
   summary(samp)

## 
## Iterations = 10001:30000
## Thinning interval = 1 
## Number of chains = 1 
## Sample size per chain = 20000 
## 
## 1. Empirical mean and standard deviation for each variable,
##    plus standard error of the mean:
## 
##                Mean       SD  Naive SE Time-series SE
## gamma[1]   0.792641 0.646869 4.574e-03      3.521e-02
## gamma[2]  -0.005295 0.640672 4.530e-03      3.552e-02
## gamma[3]   1.637455 0.644532 4.558e-03      3.664e-02
## gamma[4]  -0.193925 0.648253 4.584e-03      3.685e-02
## gamma[5]  -3.486456 0.647315 4.577e-03      3.761e-02
## gamma[6]  -3.208898 0.652157 4.611e-03      3.784e-02
## gamma[7]  -4.598029 0.646555 4.572e-03      3.636e-02
## gamma[8]  -1.152366 0.646559 4.572e-03      3.740e-02
## gamma[9]   2.394293 0.646956 4.575e-03      3.715e-02
## gamma[10]  0.487923 0.644625 4.558e-03      3.733e-02
## gamma[11]  0.460761 0.644827 4.560e-03      3.636e-02
## gamma[12]  0.833041 0.651137 4.604e-03      3.649e-02
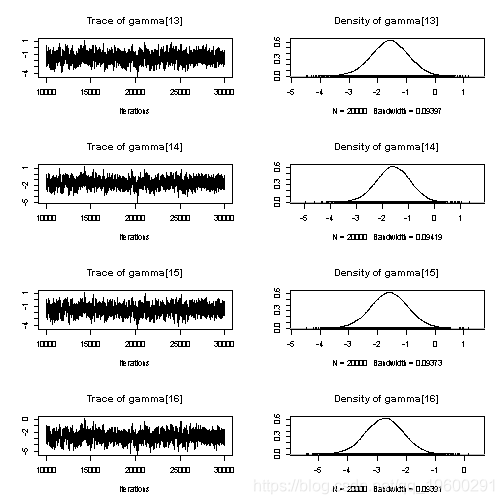
## gamma[13] -1.580735 0.651594 4.607e-03      3.672e-02
## gamma[14] -1.585905 0.647296 4.577e-03      3.760e-02
## gamma[15] -1.587356 0.647281 4.577e-03      3.744e-02
## gamma[16] -2.748602 0.644203 4.555e-03      3.740e-02
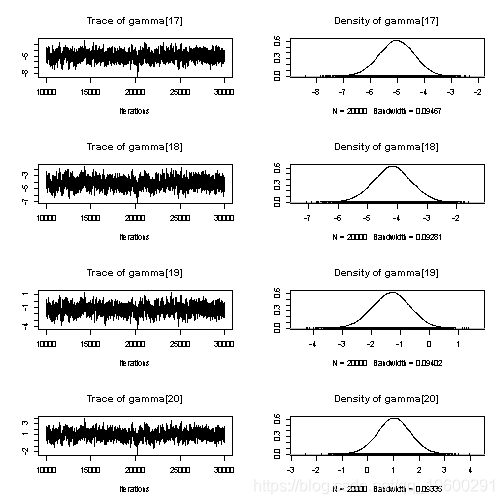
## gamma[17] -5.031267 0.647277 4.577e-03      3.710e-02
## gamma[18] -4.176877 0.648933 4.589e-03      3.655e-02
## gamma[19] -1.315643 0.648456 4.585e-03      3.730e-02
## gamma[20]  1.023326 0.648118 4.583e-03      3.502e-02
## gamma[21]  2.319419 0.652453 4.614e-03      3.625e-02
## gamma[22]  4.252081 0.642283 4.542e-03      3.672e-02
## gamma[23]  1.674201 0.648382 4.585e-03      3.726e-02
## gamma[24]  3.226205 0.649139 4.590e-03      3.647e-02
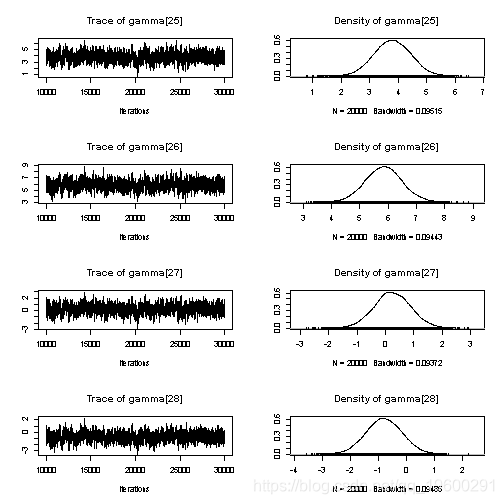
## gamma[25]  3.795414 0.650599 4.600e-03      3.717e-02
## gamma[26]  5.847544 0.653161 4.619e-03      3.616e-02
## gamma[27]  0.240722 0.651784 4.609e-03      3.609e-02
## gamma[28] -0.792185 0.649085 4.590e-03      3.542e-02
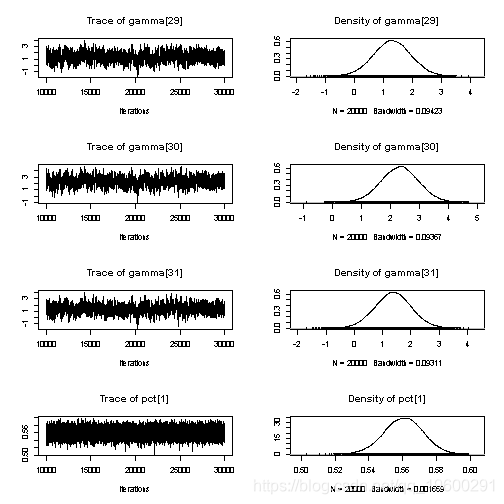
## gamma[29]  1.314577 0.648981 4.589e-03      3.578e-02
## gamma[30]  2.312463 0.643270 4.549e-03      3.774e-02
## gamma[31]  1.366669 0.645759 4.566e-03      3.719e-02
## pct[1]     0.560401 0.011415 8.072e-05      8.779e-05
## pct[2]     0.413958 0.011479 8.117e-05      9.040e-05
## pct[3]     0.025641 0.007074 5.002e-05      9.037e-05
## sigma[1]  12.948830 0.051492 3.641e-04      3.837e-04
## sigma[2]  11.130828 0.250331 1.770e-03      1.933e-03
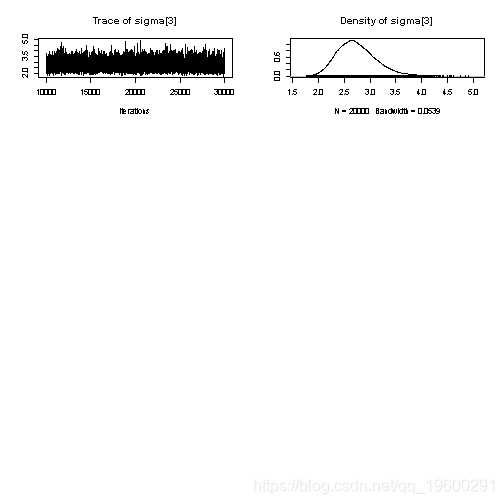
## sigma[3]   2.746672 0.378729 2.678e-03      4.721e-03
## 
## 2. Quantiles for each variable:
## 
##               2.5%      25%       50%      75%    97.5%
## gamma[1]  -0.49380  0.36017  0.791847  1.22949  2.05602
## gamma[2]  -1.29551 -0.42523  0.001094  0.42257  1.22885
## gamma[3]   0.37334  1.20738  1.636656  2.06665  2.89512
## gamma[4]  -1.48133 -0.61898 -0.193318  0.23839  1.07346
## gamma[5]  -4.77636 -3.91313 -3.479185 -3.05709 -2.23466
## gamma[6]  -4.48775 -3.64108 -3.207367 -2.77563 -1.93379
## gamma[7]  -5.87435 -5.02716 -4.594350 -4.16119 -3.34211
## gamma[8]  -2.43738 -1.57860 -1.149767 -0.71914  0.10173
## gamma[9]   1.10795  1.97121  2.394399  2.82109  3.66081
## gamma[10] -0.78684  0.05873  0.484838  0.91732  1.75985
## gamma[11] -0.81422  0.02778  0.465699  0.89415  1.72498
## gamma[12] -0.45600  0.40278  0.841823  1.27229  2.09552
## gamma[13] -2.90014 -2.00870 -1.575470 -1.14767 -0.32264
## gamma[14] -2.87864 -2.01064 -1.581978 -1.14763 -0.35096
## gamma[15] -2.86282 -2.01560 -1.583218 -1.15679 -0.32290
## gamma[16] -4.02545 -3.17798 -2.743399 -2.31751 -1.49586
## gamma[17] -6.31465 -5.46146 -5.026931 -4.59211 -3.79179
## gamma[18] -5.46025 -4.60004 -4.176324 -3.74965 -2.91543
## gamma[19] -2.60870 -1.74448 -1.305350 -0.88302 -0.06778
## gamma[20] -0.26230  0.59741  1.024962  1.45275  2.28854
## gamma[21]  1.03505  1.88831  2.319906  2.75294  3.60079
## gamma[22]  2.98850  3.82871  4.256085  4.67533  5.52185
## gamma[23]  0.38791  1.24198  1.677333  2.10926  2.93725
## gamma[24]  1.95181  2.79313  3.226292  3.65460  4.51323
## gamma[25]  2.53324  3.36055  3.793573  4.23512  5.06812
## gamma[26]  4.57296  5.41174  5.848862  6.27689  7.15103
## gamma[27] -1.03397 -0.18368  0.235404  0.67501  1.51956
## gamma[28] -2.06357 -1.22295 -0.794349 -0.35386  0.46984
## gamma[29]  0.02345  0.88405  1.316177  1.74737  2.57636
## gamma[30]  1.04671  1.88275  2.317915  2.74095  3.57092
 

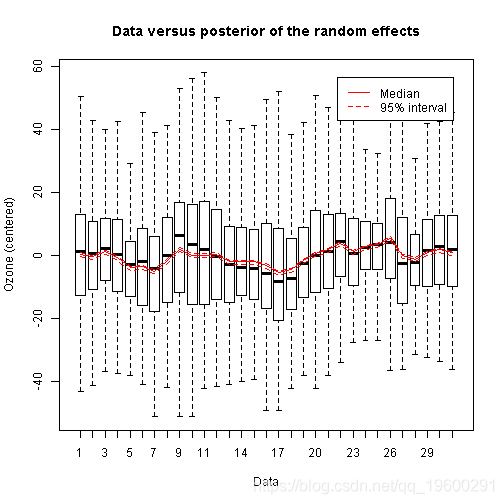
由此看来，空间位置和误差似乎是变异的最大来源，而且每日随机效应只起很小的作用。

绘制随机效果

 sum <- summary(samp)
   names(sum)
## [1] "statistics" "quantiles"  "start"      "end"        "thin"      
## [6] "nchain"
   q <- sum$quantiles

   R  <- Y-mean(Y,na.rm=TRUE)
   boxplot(R,xlab="Data",ylab="Ozone (centered)",outline=FALSE,
           main="Data versus posterior of the random effects")
   

   legend("topright",c("Median","95% interval"),lty=1:2,col=2,bg=gray(1),inset=0.05)

​

 

如果您有任何疑问，请在下面发表评论。