拓端tecdat|R语言辅导使用Metropolis- Hasting抽样算法进行逻辑回归

原文链接：http://tecdat.cn/?p=6761

 

在逻辑回归中，我们将二元因变量Y_i回归到协变量X_i上。下面的代码使用Metropolis采样来探索 beta_1和beta_2 的后验Yi到协变量Xi。

 

定义expit和分对数链接函数

1.  
   logit<-function(x){log(x/(1-x))} 此函数计算beta_1，beta_2的联合后验。它返回后验的对数以获得数值稳定性。(β1,β2)(β1,β2)。它返回后验的对数获得数值稳定性。
2.  
   log_post<-function(Y,X,beta){
3.  
   prob1 <- expit(beta[1] + beta[2]*X)
4.  
   like+prior}

这是MCMC的主要功能.can.sd是候选标准偏差。

1.  
   Bayes.logistic<-function(y,X,
2.  
   n.samples=10000,
3.  
   can.sd=0.1){
4.  
    
5.  
   keep.beta <- matrix(0,n.samples,2)
6.  
   keep.beta[1,] <- beta
7.  
    
8.  
   acc <- att <- rep(0,2)
9.  
    
10.  
    for(i in 2:n.samples){
11.  
     
12.  
    for(j in 1:2){
13.  
     
14.  
    att[j] <- att[j] + 1
15.  
     
16.  
    # 抽取候选:
17.  
     
18.  
    canbeta <- beta
19.  
    canbeta[j] <- rnorm(1,beta[j],can.sd)
20.  
    canlp <- log_post(Y,X,canbeta)
21.  
     
22.  
    # 计算接受率:
23.  
     
24.  
    R <- exp(canlp-curlp)
25.  
    U <- runif(1)
26.  
    if(U<R){
27.  
    acc[j] <- acc[j]+1
28.  
    }
29.  
    }
30.  
    keep.beta[i,]<-beta
31.  
     
32.  
    }
33.  
    # 返回beta的后验样本和Metropolis的接受率
34.  
     
35.  
     
36.  
    list(beta=keep.beta,acc.rate=acc/att)}

生成模拟数据

1.  
   set.seed(2008)
2.  
   n <- 100
3.  
   X <- rnorm(n)
4.  
   true.p <- expit(true.beta[1]+true.beta[2]*X)
5.  
   Y <- rbinom(n,1,true.p)

拟合模型

1.  
   burn <- 10000
2.  
   n.samples <- 50000
3.  
   fit <- Bayes.logistic(Y,X,n.samples=n.samples,can.sd=0.5)
4.  
   tock <- proc.time()[3]
5.  
    
6.  
   tock-tick

1.  
   ## elapsed
2.  
   ## 3.72

结果

  abline(true.beta[1],0,lwd=2,col=2)

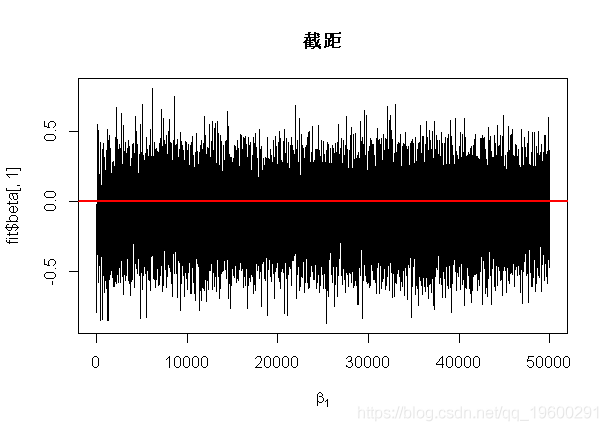
  abline(true.beta[2],0,lwd=2,col=2)

1.  
   hist(fit$beta[,1],main="Intercept",xlab=expression(beta[1]),breaks=50)
2.  
    

1.  
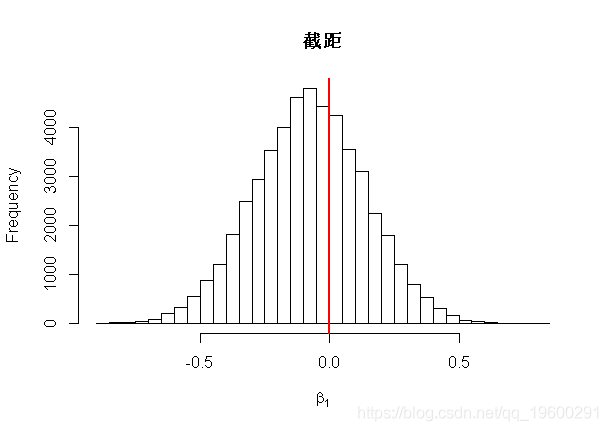
   hist(fit$beta[,2],main="Slope",xlab=expression(beta[2]),breaks=50)
2.  
   abline(v=true.beta[2],lwd=2,col=2)

1.  
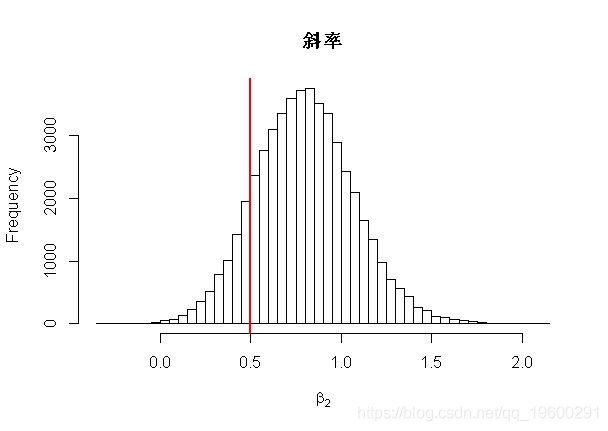
   print("Posterior mean/sd")
2.  
   ## [1] "Posterior mean/sd"
3.  
   print(round(apply(fit$beta[burn:n.samples,],2,mean),3))
4.  
   ## [1] -0.076 0.798
5.  
   print(round(apply(fit$beta[burn:n.samples,],2,sd),3))
6.  
   ## [1] 0.214 0.268
7.  
    
8.  
   ##
9.  
   ## Deviance Residuals:
10.  
    ## Min 1Q Median 3Q Max
11.  
    ## -1.6990 -1.1039 -0.6138 1.0955 1.8275
12.  
    ##
13.  
    ## Coefficients:
14.  
    ## Estimate Std. Error z value Pr(>|z|)
15.  
    ## (Intercept) -0.07393 0.21034 -0.352 0.72521
16.  
    ## X 0.76807 0.26370 2.913 0.00358 **
17.  
    ## ---
18.  
    ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
19.  
    ##
20.  
    ## (Dispersion parameter for binomial family taken to be 1)
21.  
    ##
22.  
    ## Null deviance: 138.47 on 99 degrees of freedom
23.  
    ## Residual deviance: 128.57 on 98 degrees of freedom
24.  
    ## AIC: 132.57
25.  
    ##
26.  
    ## Number of Fisher Scoring iterations: 4

 

非常感谢您阅读本文，有任何问题请在下面留言！

 

---

最受欢迎的见解

1.使用R语言进行METROPLIS-IN-GIBBS采样和MCMC运行

2.R语言中的Stan概率编程MCMC采样的贝叶斯模型

3.R语言实现MCMC中的Metropolis–Hastings算法与吉布斯采样

4.R语言BUGS JAGS贝叶斯分析 马尔科夫链蒙特卡洛方法（MCMC）采样

5.R语言中的block Gibbs吉布斯采样贝叶斯多元线性回归

6.R语言Gibbs抽样的贝叶斯简单线性回归仿真分析

7.R语言用Rcpp加速Metropolis-Hastings抽样估计贝叶斯逻辑回归模型的参数

8.R语言使用Metropolis- Hasting抽样算法进行逻辑回归

9.R语言中基于混合数据抽样(MIDAS)回归的HAR-RV模型预测GDP增长