拓端tecdat|R语言辅导中不同类型的聚类方法比较

原文链接：http://tecdat.cn/?p=6454

 

聚类方法用于识别从营销，生物医学和地理空间等领域收集的多变量数据集中的相似对象。它们是不同类型的聚类方法，包括：

  • 划分方法
  • 分层聚类
  • 模糊聚类
  • 基于密度的聚类
  • 基于模型的聚类

 

 

 

数据准备

  • 演示数据集：名为USArrest的内置R数据集
  • 删除丢失的数据
  • 缩放变量以使它们具有可比性

 

# Load  and prepare the data

my_data <- USArrests %>%
  na.omit() %>%          # Remove missing values (NA)
  scale()                # Scale variables

# View the firt 3 rows
head(my_data, n = 3)
##         Murder Assault UrbanPop     Rape
## Alabama 1.2426   0.783   -0.521 -0.00342
## Alaska  0.5079   1.107   -1.212  2.48420
## Arizona 0.0716   1.479    0.999  1.04288

距离

 

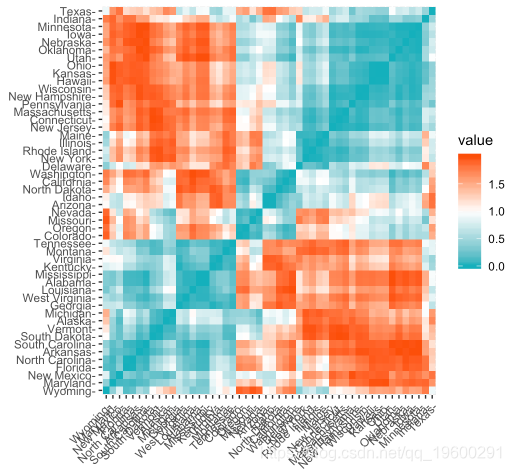
  • get_dist()：用于计算数据矩阵的行之间的距离矩阵。与标准dist()功能相比，它支持基于相关的距离测量，包括“皮尔逊”，“肯德尔”和“斯皮尔曼”方法。
  • fviz_dist()：用于可视化距离矩阵
res.dist <- get_dist(U
   gradient = list(low = "#00AFBB", mid = "white", high = "#FC4E07"))

 

​

划分聚类

、算法是将数据集细分为一组k个组的聚类技术，其中k是分析人员预先指定的组的数量。

 

k-means聚类的替代方案是K-medoids聚类或PAM（Partitioning Around Medoids，Kaufman和Rousseeuw，1990），与k-means相比，它对异常值不太敏感。

 

以下R代码显示如何确定最佳簇数以及如何在R中计算k-means和PAM聚类。

  1. 确定最佳簇数 

fviz_nbclust(my_data, kmeans, method = "gap_stat")

 

​

计算并可视化k均值聚类

set.seed(123)
 # Visualize

fviz_cluster(km.res, data = my_data,
             ellipse.type = "convex",
             palette = "jco",
             ggtheme = theme_minimal())​

 

# Compute PAM

pam.res <- pam(my_data, 3)
# Visualize
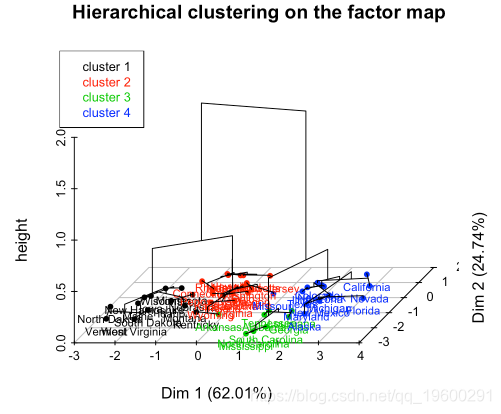
fviz_cluster(pam.res)

分层聚类

分层聚类是一种分区聚类的替代方法，用于识别数据集中的组。它不需要预先指定要生成的簇的数量。

 

# Compute hierarchical clustering
res.hc <- USArrests %>%
  scale() %>%                    # Scale the data
   hclust(method = "ward.D2")     # Compute hierachical clustering

# Visualize using factoextra
# Cut in 4 groups and color by groups
fviz_dend(res.hc, k = 4, # Cut in four groups
            color_labels_by_k = TRUE, # color labels by groups
          rect = TRUE # Add rectangle around groups
          )​

 

 

 

评估聚类倾向

为了评估聚类倾向，可以使用Hopkins的统计量和视觉方法。 

  • Hopkins统计：如果Hopkins统计量的值接近1（远高于0.5），那么我们可以得出结论，数据集是显着可聚类的。
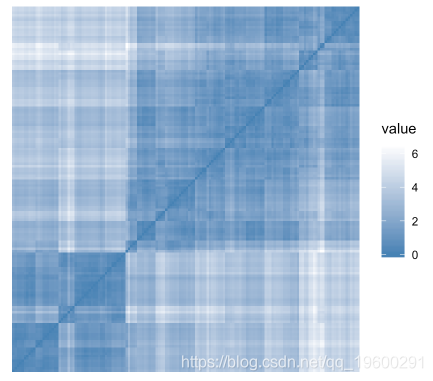
  • 视觉方法：视觉方法通过计算有序相异度图像中沿对角线的方形黑暗（或彩色）块的数量来检测聚类趋势。

R代码：

 
iris[, -5] %>%    # Remove column 5 (Species)
  scale() %>%     # Scale variables
  get_clust_tendency(n = 50, gradient = gradient.color)
## $hopkins_stat
## [1] 0.8
## 
## $plot

 

​

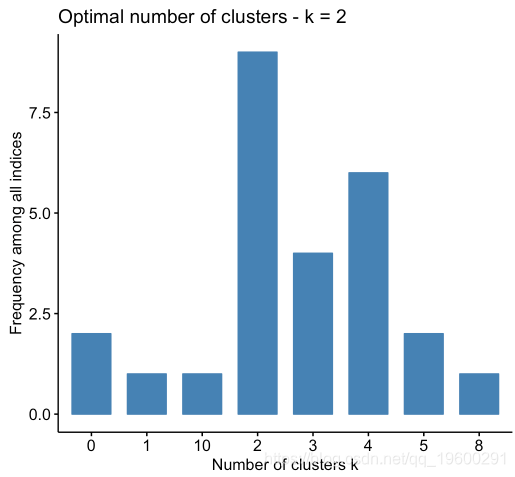
确定最佳簇数

set.seed(123)

# Compute

res.nbclust <- USArrests %>%
  scale() %>%
   (distance = "euclidean",
          min.nc = 2, max.nc = 10, 
          method = "complete", index ="all") 
# Visualize

fviz_nbclust(res.nbclust, ggtheme = theme_minimal())
## Among all indices: 
## ===================
## * 2 proposed  0 as the best number of clusters
## * 1 proposed  1 as the best number of clusters
## * 9 proposed  2 as the best number of clusters
## * 4 proposed  3 as the best number of clusters
## * 6 proposed  4 as the best number of clusters
## * 2 proposed  5 as the best number of clusters
## * 1 proposed  8 as the best number of clusters
## * 1 proposed  10 as the best number of clusters
## 
## Conclusion
## =========================
## * According to the majority rule, the best number of clusters is  2 .

 

​

群集验证统计信息

 

在下面的R代码中，我们将计算和评估层次聚类方法的结果。

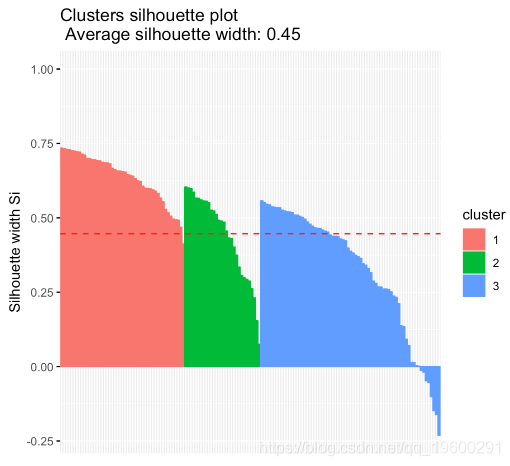
  1. 计算和可视化层次聚类：
 # Enhanced hierarchical clustering, cut in 3 groups
res.hc <- iris[, -5] %>%
  scale() %>%
   ("hclust", k = 3, graph = FALSE)

# Visualize with factoextra
 (res.hc, palette = "jco",
          rect = TRUE, show_labels = FALSE) 
​
检查轮廓图：
 (res.hc)
##   cluster size ave.sil.width
## 1       1   49          0.63
## 2       2   30          0.44
## 3       3   71          0.32

 

​

  1. 哪些样品有负面轮廓？他们更接近什么集群？
# Silhouette width of observations
sil <- res.hc$silinfo$widths[, 1:3]

# Objects with negative silhouette
neg_sil_index <- which(sil[, 'sil_width'] < 0)
sil[neg_sil_index, , drop = FALSE]
##     cluster neighbor sil_width
## 84        3        2   -0.0127
## 122       3        2   -0.0179
## 62        3        2   -0.0476
## 135       3        2   -0.0530
## 73        3        2   -0.1009
## 74        3        2   -0.1476
## 114       3        2   -0.1611
## 72        3        2   -0.2304

 

 

高级聚类方法

混合聚类方法

​

模糊聚类

模糊聚类也称为软聚类方法。标准聚类方法（K-means，PAM），其中每个观察仅属于一个聚类。这称为硬聚类。

 

 

基于模型的聚类

在基于模型的聚类中，数据被视为来自两个或多个聚类的混合的分布。它找到了最适合模型的数据并估计了簇的数量。

 

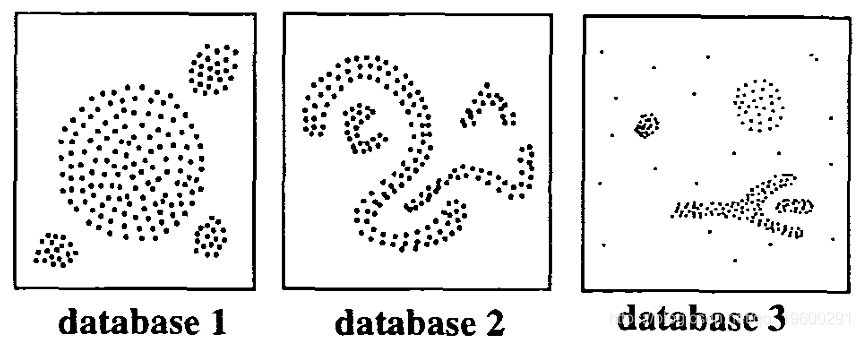
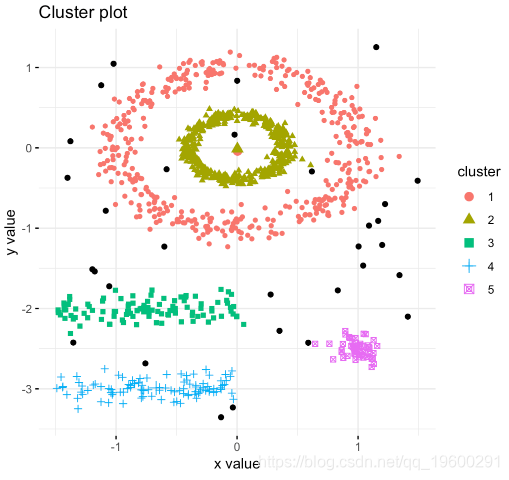
DBSCAN：基于密度的聚类

DBSCAN是Ester等人引入的聚类方法。（1996）。它可以从包含噪声和异常值的数据中找出不同形状和大小的簇（Ester等，1996）。基于密度的聚类方法背后的基本思想源于人类直观的聚类方法。

R链中的DBSCAN的描述和实现

 

​

 

​

 

如果您有任何疑问，请在下面发表评论。

 
posted @ 2019-09-09 20:45  拓端tecdat  阅读(3016)  评论(0)  编辑  收藏  举报