拓端tecdat|R语言辅导解释生存分析中危险率和风险率的变化

 原文链接：http://tecdat.cn/?p=6432

 

危险率函数

 让我们模拟R中的一些数据：

n < -  10000
h < -  0.5
t < -  -log（runif（n））/ h

该代码模拟了危险函数的存活时间，即常数。 

事件< -  1 *（t <5）
时间< -  t
obstime [obstime> = 5] < -  5

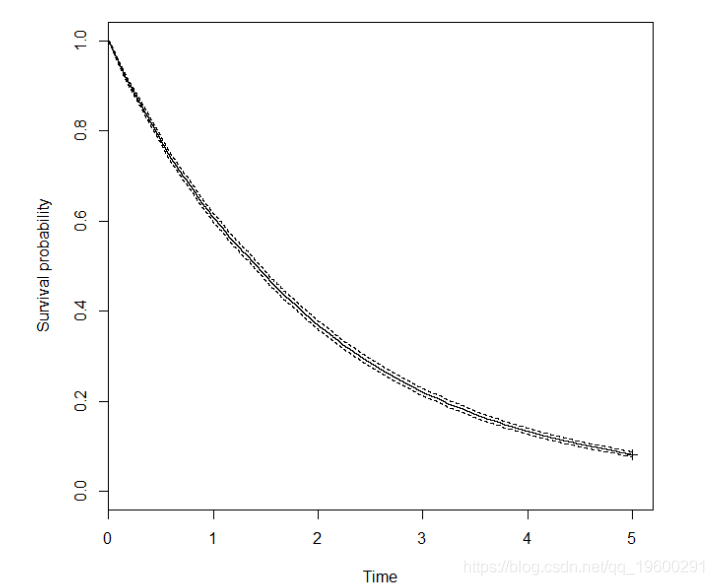
现在让我们使用R中的生存包绘制估计的生存函数：

survfit < -  survfit（Surv（obstime，event）~1）

  ​

 

 

Kaplan-Meier

 

95％置信区间限制非常接近此处的估计线，因为我们已经模拟了具有大样本量的数据集。

 

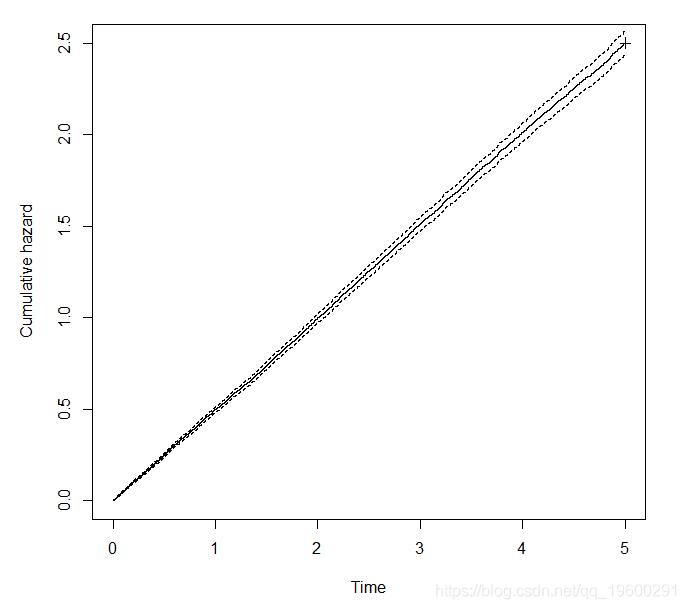
累积危险率函数

为了确定危险函数是否在变化，我们可以绘制累积危险函数，

plot（survfit，fun =“cumhaz”）

 

​

 

危险变化

有时危险函数不会是恒定的，这将导致累积危险函数的梯度/斜率随时间变化。 

我们现在将再次模拟生存时间 ：

highrisk < -  1 *（runif（n）<0.5）
h < -  0.5 + highrisk * 1.5
t < -  -log（runif（n））/ h
 
obstime [obstime> = 5] < -  5

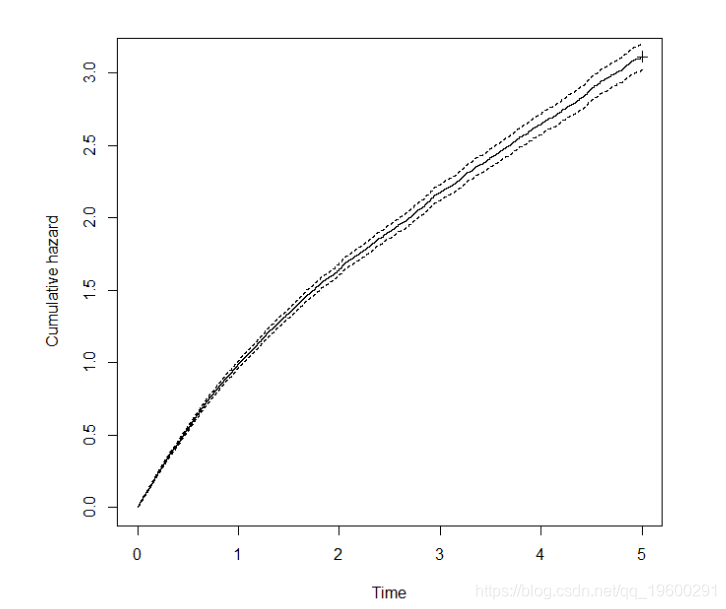
我们再次绘制累积危险函数：

​

累积危险图，其中样本由50％低风险和50％高风险对象组成

该图的自然解释是受试者经历的危险随着时间的推移而减少，因为累积危险函数的梯度/斜率随时间降低。 

 

 

改变风险比

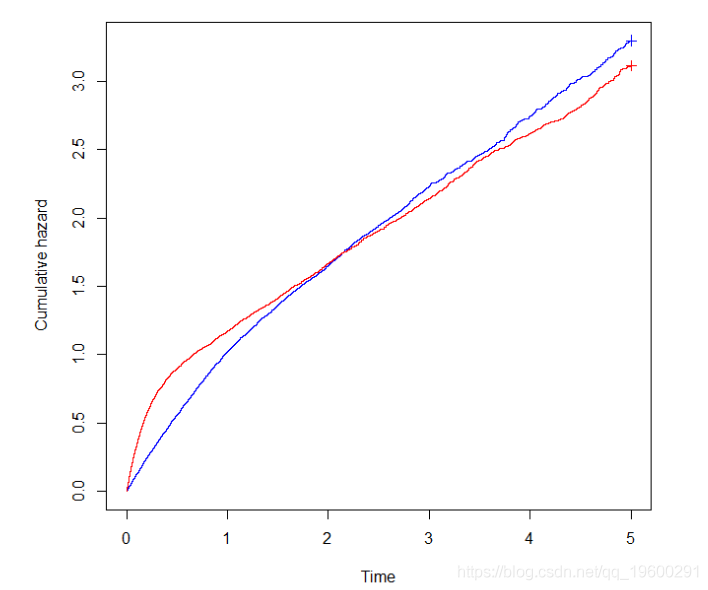
在我们比较两组生存率的研究中可能出现同样的问题，例如在比较两种治疗方案的随机试验中。这种比较通常通过估算两组之间的风险比来概括，假设两组的危害比率随着时间的推移是恒定的，使用Cox的比例风险模型。 

highrisk < -  1 *（runif（n）<0.5）
治疗< -  1 *（runif（n）<0.5）
 t < -  -log（runif（n））/ h
事件< -  1 *（t <5）
时间< -  t
obstime [obstime> = 5] < -  5

现在让我们分别按治疗组绘制累积危险函数：

 

​

 

 

 

如果您有任何疑问，请在下面发表评论。