拓端tecdat|SAS Visual Analytics代写时间序列建模三部曲
原文链接:http://tecdat.cn/?p=5202
与大多数高级分析解决方案不同,时间序列建模是一种低成本解决方案,可提供强大的洞察力。
本文将介绍构建质量时间序列模型的三个基本步骤:使数据静止不动,选择正确的模型并评估模型的准确性。这篇文章中的例子使用了一家主要汽车营销公司的历史页面浏览数据。
步骤1:
时间序列涉及使用按时间间隔(分钟,小时,天,周等)进行索引的数据。由于时间序列数据的离散性质,许多时间序列数据集都在数据中嵌入了季节和/或趋势元素。时间序列建模的第一步是考虑现有季节(固定时间段内的重复模式)和/或趋势(数据中的向上或向下移动)。考虑到这些嵌入式模式,我们称之为数据固定。下面的图1和图2可以看出趋势和季节数据的例子。
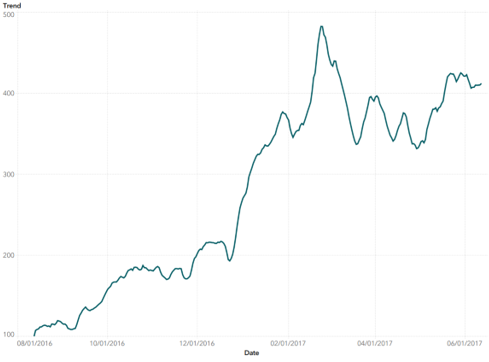
图1:向上趋势数据示例
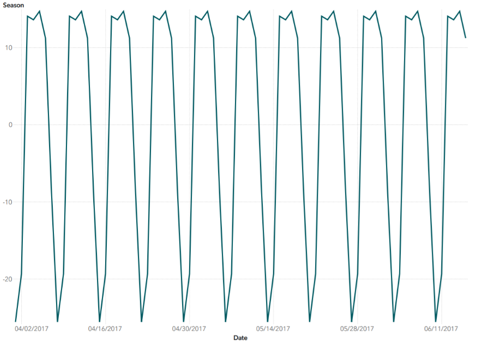
图2:季节数据示例
什么是平稳性?
正如我们前面提到的,时间序列建模的第一步是消除数据中存在的趋势或季节的影响,以使其静止不动。我们一直在抛弃术语平稳性,但究竟意味着什么?
一个固定的系列就是这个系列的平均值不再是时间的函数。有了趋势数据,随着时间的增加,该系列的平均值会随着时间的推移而增加或减少(想想随着时间的推移,房价会持续上涨)。对于季节性数据,系列的平均值会根据季节波动(考虑每24小时的温度增减)。
我们如何实现平稳?
有两种方法可用于实现平稳性,差异数据或线性回归。为了有所作为,您可以计算连续观察值之间的差异。要使用线性回归,可以在模型中包含季节性组件的二元指示符变量。在我们决定应用哪些方法之前,让我们来探索一下我们的数据。我们使用SAS Visual Analytics绘制历史日常页面浏览量。
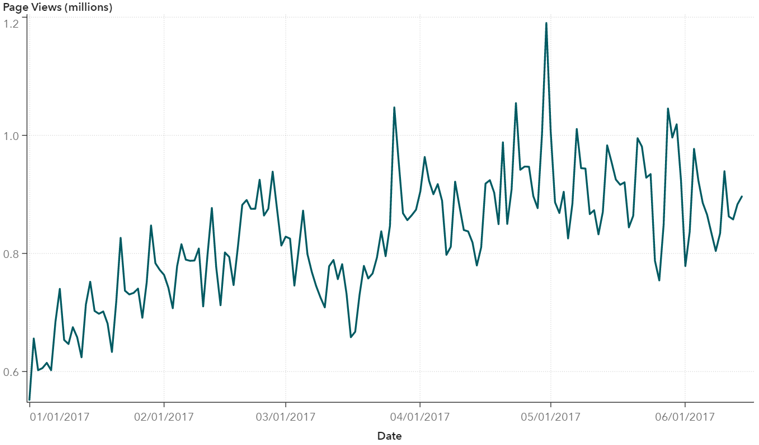
图3:原始页面视图的时间序列图
最初的模式似乎每七天重复一次,表明每周的季节。随着时间的推移浏览页面数量的持续增长表明存在略微上升的趋势。随着数据的总体思路,我们应用了平稳性统计检验,增强型Dickey-Fuller(ADF)检验。ADF测试是平稳性的单位根检验。我们在这里不会涉及细节,但是单位根表明系列是否是非平稳的,所以我们使用这个测试来确定处理趋势或季节(差异或回归)的适当方法。基于上述数据的ADF测试,我们通过在一周中的某天回归虚拟变量来移除七天的季节,并通过区分数据来消除趋势。由此产生的固定数据可以在下图中看到。
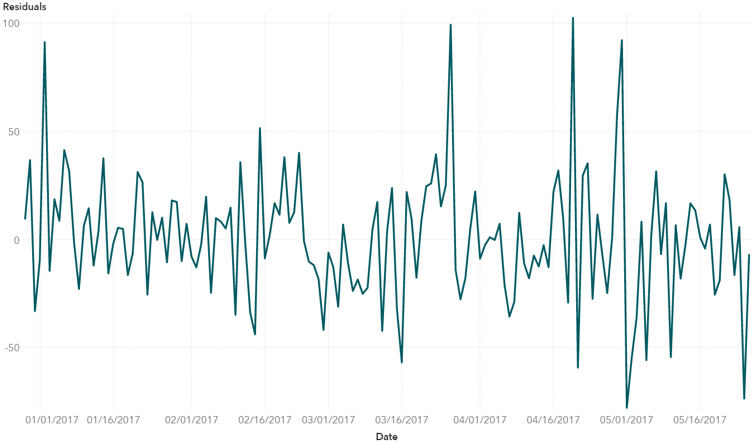
图4:删除季节和趋势后的固定数据
第2步:建立您的时间序列模型
现在数据是平稳的,时间序列建模的第二步是建立一个基准水平预测。我们还应该注意到,大多数基准级预测不需要将数据固定的第一步。这仅仅是更高级的模型所需要的,比如我们将要讨论的ARIMA建模。
建立基准预测
有几种类型的时间序列模型。要建立一个可以准确预测未来页面浏览量的模型(或者您对预测感兴趣的任何内容),有必要确定适合您数据的模型类型。
最简单的选择是假定y的未来值(您对预测感兴趣的变量)等于y的最新值。这被认为是最基本的或“天真的模式”,其中最近的观察是明天最可能的结果。
第二种类型的模型是平均模型。在这个模型中,数据集中的所有观察值都被赋予相同的权重。y的未来预测以观测数据的平均值计算。如果数据是水平的,所产生的预测可能相当准确,但如果数据趋势化或具有季节性组成部分,则会提供非常差的预测。下面可以看到使用平均模型的页面查看数据的预测值。
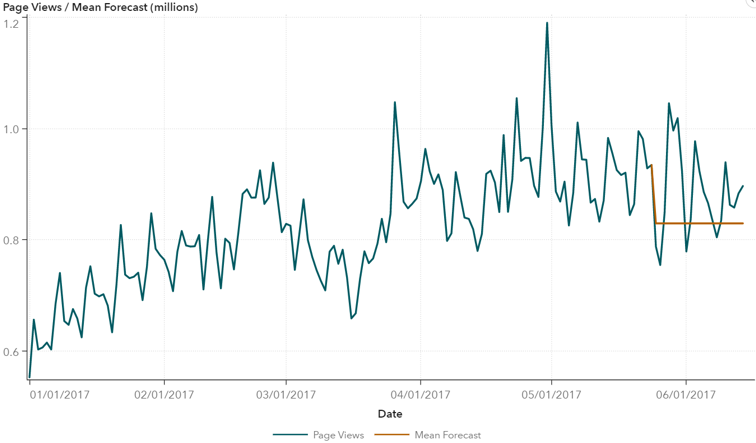
图5:平均(平均)模型预测
如果数据具有季节性或趋势元素,那么对于基准级模型来说,更好的选择是实施指数平滑模型(ESM)。ESM在上述天真模型和平均模型之间找到了一个愉快的媒介,其中最近的观测被赋予了最大的权重,并且之前所有观测的权重都呈指数级下降到过去。ESM还允许将季节性和/或趋势分量纳入模型。下表提供了初始权重0.7以0.3的比率呈指数下降的例子。
意见重量(α= 0.7)
Yt(目前的观察)0.7
YT-10.21
YT-20.063
YT-30.0189
YT-40.00567
表1:过去观察Y的指数下降效应的例子。
在时间序列预测中可以实施各种类型的ESM。使用的理想模型将取决于您拥有的数据类型。下表根据数据中的趋势和季节组合提供了使用何种类型的ESM的快速指南。
指数平滑模型的类型趋势季节
简单的ESM
线性ESMX
季节性ESMX
Winters ESMXX
表2:模型选择表
由于七天的强劲季节和数据的上升趋势,我们选择了一个冬季增温ESM作为新的基准水平模型。所产生的预测做了一个体面的工作,继续轻微的上升趋势并捕捉七天的季节。但是,数据中还有更多可以删除的模式。

图6:冬季添加剂ESM预测
ARIMA建模
在确定了最能说明数据趋势和季节的模型后,您最终将获得足够的信息来生成一个体面的预测,如上面的图2所示。然而,这些模型仍然存在局限性,因为它们没有考虑到在过去一段时间内利益变量与自身的相关性。我们将这种相关性称为自相关,它通常在时间序列数据中找到。如果数据与我们的数据具有自相关性,那么可能会进行额外的建模,以进一步改进基线预测。
为了捕获时间序列模型中自相关的影响,有必要实施自回归整合移动平均(或ARIMA)模型。ARIMA模型包含了考虑季节和趋势的参数(例如使用虚拟变量来表示一周中的天数和差异),还允许包含自回归和/或移动平均项来处理数据中嵌入的自相关。通过使用适当的ARIMA模型,我们可以进一步提高页面浏览量预测的准确性,如图3所示。

图7:季节性ARIMA模型预测
第3步:评估模型的准确性
虽然您可以看到提供的每个模型的精度都有所提高,但从视觉上确定哪个模型具有最佳精度并不总是可靠的。计算MAPE(平均绝对误差百分比)是一种快速简便的方法,可以比较所提出模型的总体预测精度 - MAPE越低预测精度越好。比较先前讨论的每个模型的MAPE,很容易看出季节性ARIMA模型提供了最佳的预测精度。请注意,还有其他几种可用于模型比较的比较统计信息。
模型错误验证
模型MAPE
Winters ESM6.9
季节性ARIMA4.4
表3:模型错误率比较
概要
总而言之,构建一个强大的时间序列预测模型的诀窍是尽可能多地消除噪音(趋势,季节和自相关),以便数据中唯一剩下的运动是纯粹的随机性。对于我们的数据,我们发现具有回归变量的季节ARIMA模型提供了最准确的预测。与上面提到的天真,平均和ESM模型相比,ARIMA模型预测更准确。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号