拓端tecdat|R语言代写对MNIST数据集分析:探索手写数字分类
原文链接:http://tecdat.cn/?p=5246
数据科学和机器学习之间区别的定义:数据科学专注于提取洞察力,而机器学习对预测有兴趣。我还注意到这两个领域大相径庭:
我在我的工作中同时使用了机器学习和数据科学:我可能会使用堆栈溢出流量数据的模型来确定哪些用户可能正在寻找工作(机器学习),但是会构建摘要和可视化来检查为什么(数据科学)。
我想进一步探讨数据科学和机器学习如何相互补充,展示我将如何使用数据科学来解决图像分类问题。我们将使用经典的机器学习挑战:MNIST数字数据库。

面临的挑战是根据28×28的黑白图像对手写数字进行分类。MNIST经常被认为是证明神经网络有效性的首批数据集之一。
预处理
默认的MNIST数据集的格式有些不方便,但Joseph Redmon已经帮助创建了CSV格式的版本。我们可以下载它的readr包。
library(readr)
library(dplyr)
mnist_raw <- read_csv("https://pjreddie.com/media/files/mnist_train.csv", col_names = FALSE)
该数据集对于60000个训练实例中的每一个包含一行,并且对于28×28图像中的784个像素中的每一个包含一列。
我们想先探索一个子集。在第一次探索数据时,您不需要完整的训练示例,因为使用子集可以快速迭代并创建概念证明,同时节省计算时间。
考虑到这一点,我们将收集数据,进行一些算术运算以跟踪图像中的x和y,并且只保留前10,000个训练实例。
library(tidyr)
pixels_gathered <- mnist_raw %>%head(10000) %>%rename(label = X1) %>%mutate(instance = row_number()) %>%gather(pixel, value, -label, -instance) %>%tidyr::extract(pixel, "pixel", "(\\d+)", convert = TRUE) %>%mutate(pixel = pixel - 2,x = pixel %% 28,y = 28 - pixel %/% 28)
pixels_gathered
## # A tibble: 7,840,000 x 6
## label instance value pixel x y
##
## 1 5 1 0 0 0 28.0
## 2 0 2 0 0 0 28.0
## 3 4 3 0 0 0 28.0
## 4 1 4 0 0 0 28.0
## 5 9 5 0 0 0 28.0
## 6 2 6 0 0 0 28.0
## 7 1 7 0 0 0 28.0
## 8 3 8 0 0 0 28.0
## 9 1 9 0 0 0 28.0
## 10 4 10 0 0 0 28.0
## # ... with 7,839,990 more rows
现在我们对每个图像中的每个像素都有一行。这是一种有用的格式,因为它可以让我们一路上看到数据。例如,我们可以用ggplot2的几行来可视化前12个实例。
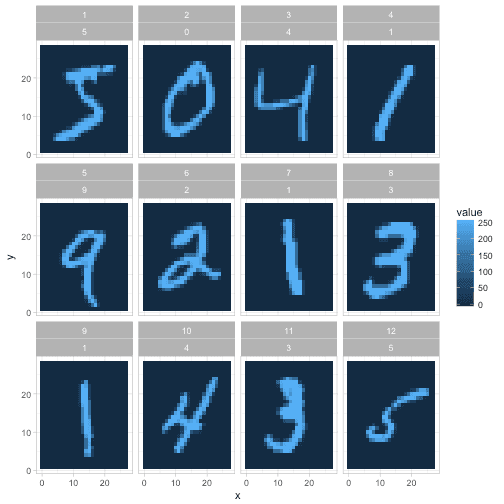
探索像素数据
这组图像中有多少灰色?
ggplot(pixels_gathered, aes(value)) +geom_histogram()
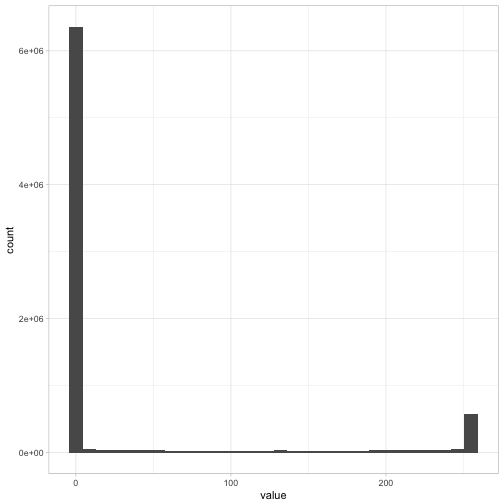
数据集中的大部分像素都是完全白色的,而另一组像素则完全是黑色的,其间相对较少。

这些平均图像称为质心。我们将每个图像视为784维点(28乘28),然后分别取每个维度中所有点的平均值。一种基本的机器学习方法,即最接近质心分类器,会要求每个图像中最接近它的这些质心中的哪一个。
非典型的例子
到目前为止,这个机器学习问题似乎有点简单:我们有一些非常“典型”的每个数字版本。但分类可能具有挑战性的原因之一是,一些数字将远远超出标准。探索非典型案例很有用,因为它可以帮助我们理解该方法失败的原因,并帮助我们选择方法和工程师功能。
在这种情况下,我们可以将每幅图像的欧几里德距离(平方和的平方根)考虑到其标签的质心。
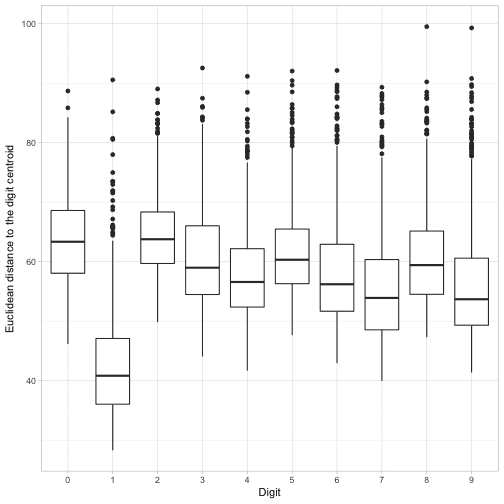
以这种方式衡量,哪些数字平均具有更多的可变性?
ggplot(image_distances, aes(factor(label), euclidean_distance)) +geom_boxplot() +labs(x = "Digit",y = "Euclidean distance to the digit centroid")
为了发现这一点,我们可以看到与中央数字最不相似的六位数字实例。

两两比较数字
为了检查这一点,我们可以尝试重叠我们的质心位数对,并考虑它们之间的差异。
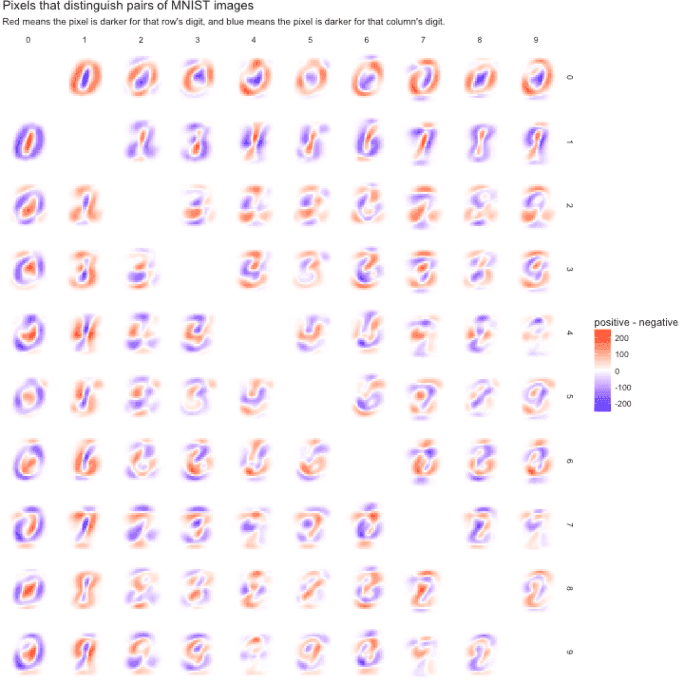
具有非常红色或非常蓝色区域的对将很容易分类,因为它们描述的是将数据集整齐划分的特征。这证实了我们对0/1易于分类的怀疑:它具有比深红色或蓝色更大的区域。