拓端tecdat|R语言代写周氏检验(Chow test) 检验回归中结构不稳定性的虚拟变量的替代方案
全球化时代快速增长的经济体之一是埃塞俄比亚经济。在低收入国家中，它已成为在国内生产总值（GDP）中实现两位数增长率的少数几个国家之一。然而，关于两位数的增长率存在很多争论，特别是在最近的全球经济衰退期间。因此，埃塞俄比亚的GDP与回归量（时间）之间的关系是否存在结构性变化，这成为一个实证研究的问题。
我们如何发现结构性变化实际上已经发生？为了回答这个问题，我们考虑了1981年至2015年期间埃塞俄比亚的国内生产总值（按2010年不变美元计算）。与世界上许多其他国家一样，埃塞俄比亚在最后一个九十年代早期采用了受管制的全球化政策。世纪。因此，我们的目标是在采取全球化政策导致重大政策转变之后，埃塞俄比亚的国内生产总值是否经历了任何结构性变化。为了回答这个问题，我们在统计和计量经济学研究中有两种选择。关于结构变化的最重要的测试类别是广义波动测试框架（Kuan和Hornik，1995）和基于F统计的测试（Hansen，1992; Andrews，1993; Andrews和Ploberger，1994）。在另一。第一类特别包括CUSUM和MOSUM测试以及波动测试，而Chow和supF测试属于后者。最近引起更多关注的一个主题是监测结构变化，即在历史阶段（没有结构变化）之后开始分析新的观测结果，并且能够在结构变化发生后尽快发现结构变化。
让我们将整个研究期分为两个子时期
- 1.全球化前（1981年 - 1991年）
2。全球化后（1992-2015）
整个时期的回归假设两个时间段之间没有差异，因此估计整个时期的GDP增长率。换句话说，这种回归假定截距以及斜率系数在整个时期内保持不变; 也就是说，没有结构上的变化。如果这是，事实上，这种情况，则
β01=β02=β0 and β11=β12=β1β01=β02=β0 and β11=β12=β1
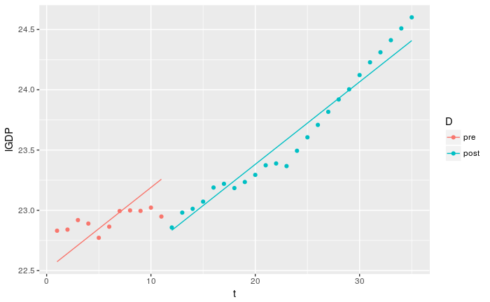
前两个回归线假设回归参数在两个子周期中是不同的，即，由于斜率参数或截距参数的变化，存在结构不稳定性。
解决方案
要应用Chow测试来根据经验可视化结构变化，需要以下假设：
- 1两个子周期回归的误差项通常以相同的方差分布;
2 这两个错误术语是独立分布的。
3应该先了解待检查结构稳定性的断点。
现在，如果这个F检验是显着的，我们可以拒绝没有结构不稳定的零假设，并得出结论，波动是GGP高到足以认为它导致GDP增长路径中的结构不稳定。
将数据导入R
gdp<-read.csv(file.choose(), sep = ",", header = TRUE)
attach(gdp)
gdp$lGDP<-log(GDP)
attach(gdp)
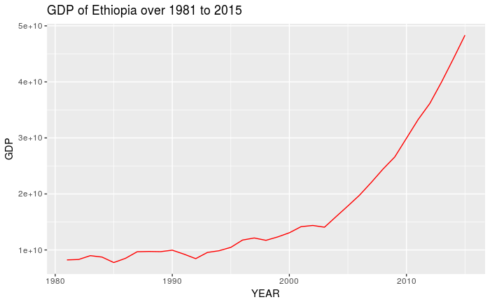
让我们看一下使用ggplot2包的GDP与时间的分散图
正如从数字中观察到的那样，在新政策制度通过后，特别是在2000年之后，国内生产总值的增长势头增强。直到1992 - 93年，由于GDP曲线或多或少与x平行，经济看起来停滞不前。 -轴。只有在1993年以后，国内生产总值才开始增长，2000年后增长变得更加突出。为了证实这一点，我们将考虑1992年埃塞俄比亚采用新经济政策时的断点来应用周氏检验。政府。
为了通过假设模型中没有结构不稳定来拟合GDP增长路径模型，我们需要通过使用以下代码来创建时间变量：
gdp $ t <-seq（1:35）
用于估算整个期间GDP的增长
残差：
Min 1Q Median 3Q Max
-0.28379 -0.17673 0.01783 0.16134 0.34789
系数：
估计标准。误差t值Pr（> | t |）
（拦截）22.495383 0.066477 338.4 <2e-16 ***
t 0.050230 0.003221 15.6 <2e-16 ***
---
Signif。代码：0'***'0.001'**'0.01'*'0.05'。' 0.1''1
残余标准误差：33自由度0.1924
多个R平方：0.8805，调整后的R平方：0.8769
F统计量：243.2 on 1和33 DF，p值：<2.2e-16
因此，我们看到，在整个时期内，国内生产总值的年增长率为5％。
我们将使用此对象'model0'在R中应用Chow测试。
断点发生在1992年，与1981年至2015年相应的序列1至35中的12个重合。代码和结果如下所示：
Chow测试
data：log（gdp_ethio）~t
F = 51.331，p值= 1.455e-10
上述结果表明，F值为51.331，相应的p值远小于显着性水平（0.05），表明测试显着。这证实了埃塞俄比亚在1992年断点处的GDP增长路径存在结构性不稳定性。
然而，我们无法判断这两个回归的差异是由于截距项或斜率系数的差异还是两者。通常这种知识本身非常有用。为了分析这种情况，我们有以下四种可能性：
I。重合回归，其中截距和斜率系数在两个子周期回归中是相同的;
II。平行回归，其中只有两个回归中的截距不同但斜率相同;
III。并发回归两个回归中的截距相同，但斜率不同; 和
IV。Dis-similar回归，其中两个回归中的截距和斜率都不同。
让我们逐个审查。
II 平行回归，其中只有两个回归中的截距不同但斜率相同
R代码和解释如下：
残差：
Min 1Q Median 3Q Max
-0.309808 -0.080889 0.006459 0.087419 0.257020
系数：
估计标准。误差t值Pr（> | t |）
（ 22.505310 0.046417 484.847 <2e-16 ***
t 0.068431 0.003783 18.089 <2e-16 ***
Dpost -0.492244 0.082302 -5.981 1.15e-06 ***
---
Signif。代码：0'***'0.001'**'0.01'*'0.05'。' 0.1''1
残余标准误差：32自由度为0.1343
多个R平方：0.9436，调整后的R平方：0.9401
F统计量：267.6 on 2和32 DF，p值：<2.2e-16
ˆlGDP=22.505+0.068t−0.492DlGDP^=22.505+0.068t−0.492D
ˆlGDP=22.013+0.068tlGDP^=22.013+0.068t
ˆlGDP=22.505+0.068tlGDP^=22.505+0.068t
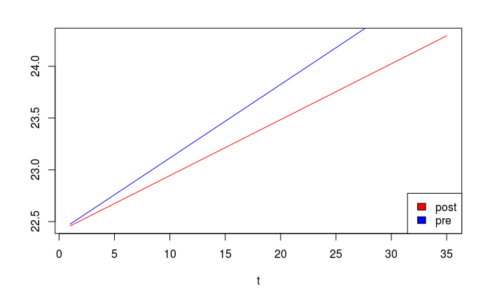
要以图形方式显示此信息，请使用以下代码生成以下图表：
g
给出这个情节：
III 并发回归，其中两个回归中的截距相同，但斜率不同
必要的R代码和结果如下：
残差：
Min 1Q Median 3Q Max
-0.26778 -0.14726 -0.04489 0.13919 0.35627
系数：
估计标准。误差t值Pr（> | t |）
（ 截）22.40377 0.09125 245.521 <2e-16 ***
t 0.07072 0.01458 4.851 3.06e-05 ***
tD -0.01721 0.01195 -1.440 0.16
---
Signif。代码：0'***'0.001'**'0.01'*'0.05'。' 0.1''1
残余标准误差：32自由度为0.1894
多个R平方：0.8878，调整后的R平方：0.8808
F统计量：126.6 on 2和32 DF，p值：6.305e-16
在上述结果中，显然相互作用项（tD）在统计学上不显着，因为相应的p值远高于显着性水平（5％或0.05）。这意味着经济改革不会影响斜率。
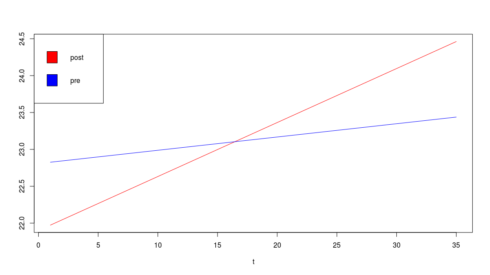
请注意，斜率，而不是增长函数的截距发生了变化。这可以用图形方式显示如下：
IV 不相似 回归（截距和斜率都不同）
在这种情况下，生长函数的截距和斜率同时改变。捕获这种变化的统计模型可以用以下等式表示。
用于捕获这种变化的修改的统计模型可以由以下等式表示。
残差：
Min 1Q Median 3Q Max
-0.21768 -0.05914 0.01033 0.07033 0.13777
系数：
估计标准。误差t值Pr（> | t |）
（拦截）22.807568 0.060484 377.084 <2e-16 ***
t 0.018055 0.008918 2.025 0.0516。
Dpost -0.907739 0.090685 -10.010 3.13e-11 ***
t：Dpost 0.055195 0.009335 5.913 1.57e-06 ***
---
Signif。代码：0'***'0.001'**'0.01'*'0.05'。' 0.1''1
残余标准误差：31自由度下0.09353
多个R平方：0.9735，调整后的R平方：0.9709
F统计量：3和31 DF为379.4，p值：<2.2e-16
为了使问题可视化，以下代码用于生成下图。
