3D 飞行器航迹规划
3D-Route-Planning
三维航迹规划 -Matlab
本次代码主要解决数学建模中多约束条件下的航迹规划问题
解决的问题如下：
复杂环境下航迹快速规划是智能飞行器控制的一个重要课题。由于系统结构限制， 这类飞行器的定位系统无法对自身进行精准定位， 一旦定位误差积累到一定程度可能导致任务失败。 因此， 在飞行过程中对定位误差进行校正是智能飞行器航迹规划中一项重要任务。
假设飞行器的飞行区域如图 1 所示， 出发点为 A 点，目的地为 B 点。 其航迹约束如下：
-
飞行器在空间飞行过程中需要实时定位，其定位误差包括垂直误差和水平误差。 飞行器每飞行 1m，垂直误差和水平误差将各增加δ个专用单位,，以下简称单位。 到达终点时垂直误差和水平误差均应小于�个单位，并且为简化问题，假设当垂直误差和水平误差均小于�个单位时，飞行器仍能够按照规划路径飞行。
-
飞行器在飞行过程中需要对定位误差进行校正。 飞行区域中存在一些安全位置（称之为校正点） 可用于误差校正， 当飞行器到达校正点即能够根据该位置的误差校正类型进行误差校正。 校正垂直和水平误差的位置可根据地形在航迹规划前确定（如图 1 为某条航迹的示意图, 黄色的点为水平误差校正点， 蓝色的点为垂直误差校正点，出发点为 A 点，目的地为 B 点，黑色曲线代表一条航迹）。 可校正的飞行区域分布位置依赖于地， 无统一规律。 若垂直误差、水平误差都能得到及时校正，则飞行器可以按照预定航线飞行，通过若干个校正点进行误差校正后最终到达目的地。
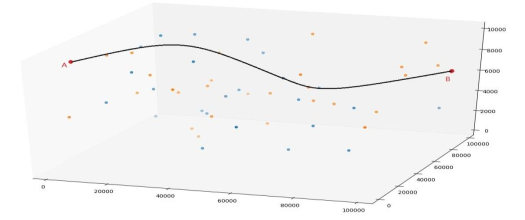
图 1 航迹规划示意图
-
在出发地 A 点，飞行器的垂直和水平误差均为 0。
-
飞行器在垂直误差校正点进行垂直误差校正后， 其垂直误差将变为 0，水 平误差保持不变。
-
飞行器在水平误差校正点进行水平误差校正后， 其水平误差将变为 0，垂 直误差保持不变。
-
当飞行器的垂直误差不大于α1个单位，水平误差不大于α2个单位时才能进 行垂直误差校正。
-
飞行器的垂直误差不大于β1个单位，水平误差不大于β2个单位时才能进 行水平误差校正。
-
飞行器在转弯时受到结构和控制系统的限制， 无法完成即时转弯(飞行器前 进方向无法突然改变)， 假设飞行器的最小转弯半径为 200m。
