(笔记)六自由度机械臂运动学分析及其轨迹规划


六自由度机械臂运动学分析


本文以6R机械臂为研究对象，采用改进D－H 模型进行运动学分析、求解。
 
1.1 机械臂结构参数
 
该机械臂 6 个关节都是转动关节，前 3 个关节确定手腕参考点的位置，后 3个关节确定手腕的方位。和大多数工业机器人一样，后 3 个关节轴线交于一点。因此将该点作为手腕的参考点，也选作为连杆坐标系{4},{5}和{6}的原点。如下图示。

对于机械臂， 通常将之看作“连杆结构” ，连杆是由关节组合而成。因此在分析机械臂的时候需要为机械手的每一连杆建立一个坐标系。

 
在分析连杆坐标系时， 通常需要在每个连杆上定义一个固连的坐标系来表明每个连杆与相邻连杆之间的相对位置关系。基于此原则， 我们首先为各连杆和关节进行编号， 然后采用由下而上的顺序，基座为连杆 0，从基座起依次向上为连杆 1、连杆 2、 …， 关节i 连接连杆i-1和i 。 
 
最终建立与连杆固连的坐标系OiXi Yi Zi ，如下所示：
 

 


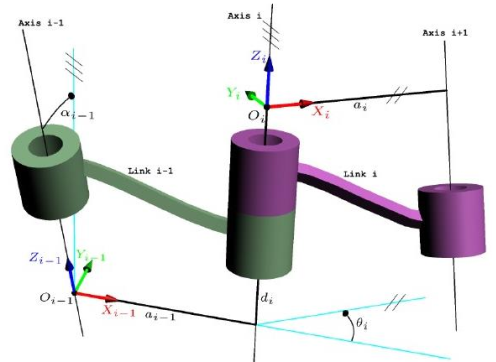
根据所设定的连杆坐标系， 相应的连杆参数可定义如下：
 
（1） 绕 xi-1轴旋转αi-1角， 可使 zi-1轴与 zii轴同一平面；
（2）沿 xii-1轴平移距离αi-1， 可使 zi-1轴与 zi 轴同一高度上；
（3）绕 zi 轴旋转θi 角， 可使 xi-1轴与 xi 轴同一直线上；
（4）沿 zi 轴平移距离 di， 可使连杆i -1的坐标系移动到其原点与连杆i 坐标系原点重合。
 
可根据改进的 D－H 示法， 对机械臂建立坐标系。在改进 D-H 坐标系中， 坐标系{0}和{1}一般重合， O1 为轴 1 和轴 2 公法线在轴 1 上的交点，此时关节 1 和关节 2 在 z 轴向上的偏置没有体现出来， 但对于整个机械臂各关节的相对运动来说并没有影响。
 
 选取第一关节坐标系与基坐标系重合。根据机械臂的结构和连杆坐标系，可得出其连杆参数和关节变量，如下表示：
 

 


 
1.2 运动学正解
 
由上述的相邻连杆的运动关系可知， 连杆i 在杆件坐标系i -1中的相对位姿可用 4 个齐次变换矩阵来描述， 如下矩阵表示为:
 

 

 
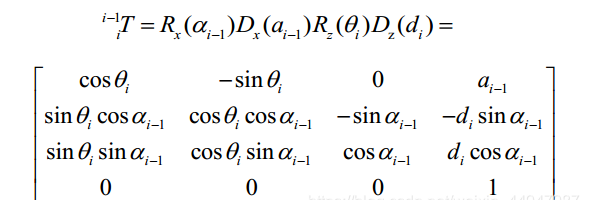
因此，机械臂的末端执行器坐标系相对于基座标系的变换矩阵为：
 

 


 
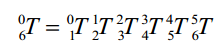
从而在得知各关节角度的情况下，可求得机器人末端执行器的位姿。


 
1.3 运动学逆解
 
机械臂的逆运动学问题， 是指已知机械臂的末端位姿， 即已知齐次变换矩阵，求解各转动关节的角度。
 
因此机械臂的逆运动学问题， 可以理解为通过正运动学方程求解关节的 θ1 、θ2 、θ3 、θ4 、θ5 、θ6 。
 
▍六自由度机械臂轨迹规划
 
对串联机械臂而言，轨迹规划可以分为：关节空间轨迹规划和笛卡尔空间轨迹规划。关节空间轨迹规划是把机器人的关节变量变换成跟时间的函数，然后对角速度和角加速度进行约束。
 
笛卡尔空间轨迹规划是把机器人末端在笛卡尔空间的位移、速度和加速度变换成跟时间的函数关系。
 
由于在关节空间中进行轨迹规划是直接用运动时的受控变量规划轨迹，有着计算量小，容易实时控制，而且不会发生机构奇异性等优点，所以经常被采用。
 
现以一维的轨迹为研究对象，利用三次多项式插值法和五次多项式插值法分别对其进行轨迹规划，通过对比两种插值法的效果，选取效果更优者对六自由度机械臂进行轨迹规划。
 

 


 
2.1 三次多项式插值法
 
三次多项式有4个待定系数，可同时对起始点和目标点的角度和角速度给出约束条件。
 
数学推导
 

 



 
MATLAB代码
 

%三次多项式插值法
clear;
clc;
q_array=[0,50,150,100,0];%指定起止位置
t_array=[0,2,4,8,10];%指定起止时间
v_array=[0,10,20,-15,0];%指定起止速度
t=[t_array(1)];q=[q_array(1)];v=[v_array(1)];a=[0];%初始状态
for i=1:1:length(q_array)-1%每一段规划的时间
     a0=q_array(i);
     a1=v_array(i);
     a2=(3/(t_array(i+1)-t_array(i))^2)*(q_array(i+1)-q_array(i))-(1/(t_array(i+1)-t_array(i)))*(2*v_array(i)+v_array(i+1));
     a3=(2/(t_array(i+1)-t_array(i))^3)*(q_array(i)-q_array(i+1))+(1/(t_array(i+1)-t_array(i))^2)*(v_array(i)+v_array(i+1));
     ti=t_array(i)+0.001:0.001:t_array(i+1);
     qi=a0+a1*(ti-t_array(i))+a2*(ti-t_array(i)).^2+a3*(ti-t_array(i)).^3;
     vi=a1+2*a2*(ti-t_array(i))+3*a3*(ti-t_array(i)).^2;
     ai=2*a2+6*a3*(ti-t_array(i));
     t=[t,ti];q=[q,qi];v=[v,vi];a=[a,ai];
end
subplot(3,1,1),plot(t,q,'r'),xlabel('t/s'),ylabel('p/m');hold on; plot(t_array,q_array,'o','color','r'),grid on;
subplot(3,1,2),plot(t,v,'b'),xlabel('t/s'),ylabel('v/(m/s)');hold on;plot(t_array,v_array,'*','color','r'),grid on;
subplot(3,1,3),plot(t,a,'g'),xlabel('t/s'),ylabel('a/(m/s^2)');hold on;
% 指定文件夹保存图片
filepath=pwd;           %保存当前工作目录
cd('C:\Users\Administrator\Desktop\pic')                %把当前工作目录切换到图片存储文件夹
print(gcf,'-djpeg','C:\Users\Administrator\Desktop\pic\san.jpeg'); %将图片保存为jpg格式，
cd(filepath)            %切回原工作目录

 

 


 
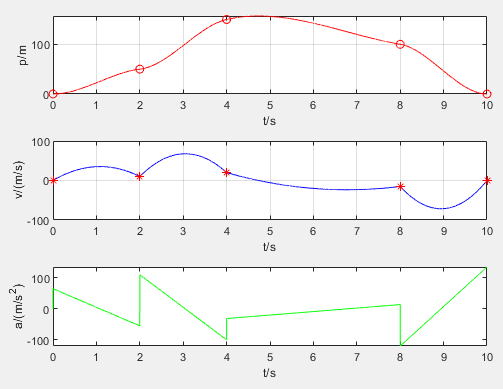
2.2 五次多项式插值法
 
五次多项式有6个待定系数，可同时对起始点和目标点的角度、角速度和角加速度给出约束条件。
 
数学推导
 

 



 

MATLAB代码
 

%五次多项式插值法
clear;
clc;
q_array=[0,50,150,100,40];%指定起止位置
t_array=[0,3,6,12,14];%指定起止时间
v_array=[0,10,20,-15,0];%指定起止速度
a_array=[0,20,30,-20,0];%指定起止加速度
t=[t_array(1)];q=[q_array(1)];v=[v_array(1)];a=[a_array(1)];%初始状态
for i=1:1:length(q_array)-1%每一段规划的时间
     T=t_array(i+1)-t_array(i);
     a0=q_array(i);
     a1=v_array(i);
     a2=a_array(i)/2;
     a3=(20*q_array(i+1)-20*q_array(i)-(8*v_array(i+1)+12*v_array(i))*T-(3*a_array(i)-a_array(i+1))*T^2)/(2*T^3);
     a4=(30*q_array(i)-30*q_array(i+1)+(14*v_array(i+1)+16*v_array(i))*T+(3*a_array(i)-2*a_array(i+1))*T^2)/(2*T^4);
     a5=(12*q_array(i+1)-12*q_array(i)-(6*v_array(i+1)+6*v_array(i))*T-(a_array(i)-a_array(i+1))*T^2)/(2*T^5);%计算五次多项式系数 
     ti=t_array(i):0.001:t_array(i+1);
     qi=a0+a1*(ti-t_array(i))+a2*(ti-t_array(i)).^2+a3*(ti-t_array(i)).^3+a4*(ti-t_array(i)).^4+a5*(ti-t_array(i)).^5;
     vi=a1+2*a2*(ti-t_array(i))+3*a3*(ti-t_array(i)).^2+4*a4*(ti-t_array(i)).^3+5*a5*(ti-t_array(i)).^4;
     ai=2*a2+6*a3*(ti-t_array(i))+12*a4*(ti-t_array(i)).^2+20*a5*(ti-t_array(i)).^3;
     t=[t,ti(2:end)];q=[q,qi(2:end)];v=[v,vi(2:end)];a=[a,ai(2:end)];
end
subplot(3,1,1),plot(t,q,'r'),xlabel('t/s'),ylabel('p/m');hold on; plot(t_array,q_array,'o','color','r'),grid on;
subplot(3,1,2),plot(t,v,'b'),xlabel('t/s'),ylabel('v/(m/s)');hold on;plot(t_array,v_array,'*','color','r'),grid on;
subplot(3,1,3),plot(t,a,'g'),xlabel('t/s'),ylabel('a/(m/s^2)');hold on;plot(t_array,a_array,'^','color','r'),grid on;
% 指定文件夹保存图片
filepath=pwd;           %保存当前工作目录
cd('C:\Users\Administrator\Desktop\pic')                %把当前工作目录切换到图片存储文件夹
print(gcf,'-djpeg','C:\Users\Administrator\Desktop\pic\wu.jpeg'); %将图片保存为jpg格式，
cd(filepath)            %切回原工作目录

 

 

 
2.3 两种插值法的效果对比
 
相对于三次多项式插值， 五次多项式插值法所得到的轨迹加速度也是平滑的曲线，并没有出现跳变的情况。
 
在机器人系统中，关节角加速度出现跳变现象意味着关节的电机会受到冲击， 因此为保证电机平稳运行，角加速度要求平滑连续。
 
虽然三次多项式插值法的计算量和较之更小，但对于离线规划而言，该时间成本可以忽略，因此从规划的轨迹平稳度而言，五次多项式插值法更佳。
 
▍六自由度机械臂轨迹规划仿真
 
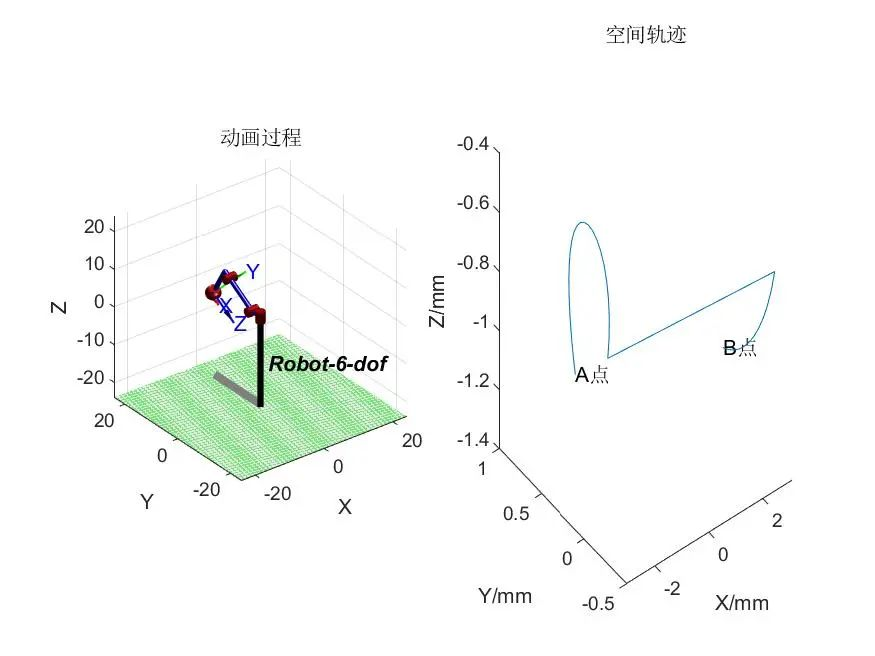
采用五次多项式插值法进行机械臂轨迹规划，基于Matlab Robotics Toolbox平台进行关节空间轨迹规划，得到各关节角度、速度和加速度与时间关系曲线。
 
需要注意的是，利用Robotics Toolbox进行轨迹规划前，需要安装工具箱，可参考以下博客：
https://blog.csdn.net/qq_25267657/article/details/87948987
 
此外，每次重新启动MATLAB时都需要重新输入“startup_rvc”回车来启动这个工具箱。
 
本文所控对象为串联六R机械臂，其具体尺寸参数见于代码中的D-H表。
 
MATLAB代码

% Modified DH
% ABB robot
% lujingguihua
clear;
clc;
% %机器人建模
th(1) = 0; d(1) = 0; a(1) = 0; alp(1) = 0;
th(2) = 0; d(2) = 0; a(2) = 3.20; alp(2) = pi/2;   
th(3) = 0; d(3) = 0; a(3) = 9.75; alp(3) = 0;
th(4) = 0; d(4) = 8.87; a(4) = 2; alp(4) = pi/2;
th(5) = 0; d(5) = 0; a(5) = 0; alp(5) = -pi/2;
th(6) = 0; d(6) = 0; a(6) = 0; alp(6) = pi/2;
% DH parameters  th     d    a    alpha  sigma
L1 = Link([th(1), d(1), a(1), alp(1), 0], 'modified');
L2 = Link([th(2), d(2), a(2), alp(2), 0], 'modified');
L3 = Link([th(3), d(3), a(3), alp(3), 0], 'modified');
L4 = Link([th(4), d(4), a(4), alp(4), 0], 'modified');
L5 = Link([th(5), d(5), a(5), alp(5), 0], 'modified');
L6 = Link([th(6), d(6), a(6), alp(6), 0], 'modified');
robot = SerialLink([L1, L2, L3, L4, L5, L6]); %SerialLink 类函数
robot.name='Robot-6-dof';
robot.display(); %显示D-H表

%轨迹规划参数设置
init_ang = [pi/6,0, 2*pi/3,pi/3, 0, 0];
targ_ang = [pi/2,pi/6,0,0, -pi/2, pi/6];
T =(0:0.1:5);
%关节空间轨迹规划方法
[q,qd,qdd] = jtraj(init_ang,targ_ang,T); %直接得到角度、角速度、角加速度的的序列

%%显示
figure(1);
%动画显示
subplot(1,2,1); 
title('动画过程');
robot.plot(q);
% 轨迹显示
t=robot.fkine(q);%运动学正解
rpy=tr2rpy(t);  %t中提取位置（xyz）
subplot(1,2,2);
plot2(rpy);
xlabel('X/mm'),ylabel('Y/mm'),zlabel('Z/mm');hold on
title('空间轨迹');
text(rpy(1,1),rpy(1,2),rpy(1,3),'A点');
text(rpy(51,1),rpy(51,2),rpy(51,3),'B点');
% 指定文件夹保存图片
filepath=pwd;           %保存当前工作目录
cd('C:\Users\Administrator\Desktop\pic')                %把当前工作目录切换到图片存储文件夹
print(gcf,'-djpeg','C:\Users\Administrator\Desktop\pic\1.jpeg'); %将图片保存为jpg格式，
cd(filepath)            %切回原工作目录

%单个关节的位置title('关节1位置');
figure(2);
subplot(3,2,1);
plot(T,q(:,1));
xlabel('t/s'),ylabel('θ1/rad');hold on
subplot(3,2,2);
plot(T,q(:,2));
xlabel('t/s'),ylabel('θ2/rad');hold on
subplot(3,2,3);
plot(T,q(:,3));
xlabel('t/s'),ylabel('θ3/rad');hold on
subplot(3,2,4);
plot(T,q(:,4));
xlabel('t/s'),ylabel('θ4/rad');hold on
subplot(3,2,5);
plot(T,q(:,5));
xlabel('t/s'),ylabel('θ5/rad');hold on
subplot(3,2,6);
plot(T,q(:,6));
xlabel('t/s'),ylabel('θ6/rad');hold on
% 指定文件夹保存图片
filepath=pwd;           %保存当前工作目录
cd('C:\Users\Administrator\Desktop\pic')                %把当前工作目录切换到图片存储文件夹
print(gcf,'-djpeg','C:\Users\Administrator\Desktop\pic\2.jpeg'); %将图片保存为jpg格式，
cd(filepath)            %切回原工作目录

%单个关节的速度
figure(3);
subplot(3,2,1);
plot(T,qd(:,1));
xlabel('t/s'),ylabel('Ω1/rad');hold on
subplot(3,2,2);
plot(T,qd(:,2));
xlabel('t/s'),ylabel('Ω2/rad');hold on
subplot(3,2,3);
plot(T,qd(:,3));
xlabel('t/s'),ylabel('Ω3/rad');hold on
subplot(3,2,4);
plot(T,qd(:,4));
xlabel('t/s'),ylabel('Ω4/rad');hold on
subplot(3,2,5);
plot(T,qd(:,5));
xlabel('t/s'),ylabel('Ω5/rad');hold on
subplot(3,2,6);
plot(T,qd(:,6));
xlabel('t/s'),ylabel('Ω6/rad');hold on
% 指定文件夹保存图片
filepath=pwd;           %保存当前工作目录
cd('C:\Users\Administrator\Desktop\pic')                
%把当前工作目录切换到图片存储文件夹
print(gcf,'-djpeg','C:\Users\Administrator\Desktop\pic\3.jpeg'); %将图片保存为jpg格式，
cd(filepath)            %切回原工作目录

%单个关节的加速度
figure(4);
subplot(3,2,1);
plot(T,qdd(:,1));
xlabel('t/s'),ylabel('α1/rad');hold on
subplot(3,2,2);
plot(T,qdd(:,2));
xlabel('t/s'),ylabel('α2/rad');hold on
subplot(3,2,3);
plot(T,qdd(:,3));
xlabel('t/s'),ylabel('α3/rad');hold on
subplot(3,2,4);
plot(T,qdd(:,4));
xlabel('t/s'),ylabel('α4/rad');hold on;
subplot(3,2,5);
plot(T,qdd(:,5));
xlabel('t/s'),ylabel('α5/rad');hold on
subplot(3,2,6);
plot(T,qdd(:,6));
xlabel('t/s'),ylabel('α6/rad');hold on
% 指定文件夹保存图片
filepath=pwd;           %保存当前工作目录
cd('C:\Users\Administrator\Desktop\pic')                %把当前工作目录切换到图片存储文件夹
print(gcf,'-djpeg','C:\Users\Administrator\Desktop\pic\4.jpeg'); %将图片保存为jpg格式，
cd(filepath)            %切回原工作目录

 

 

 

 


 ▍结论

  1. 通过轨迹规划，不仅得到了机械臂末端执行器的空间轨迹，还可以得到其关节的角位移、角速度和角加速度。从上图 可以看出机械臂到达预定的位置，证明了该机械臂设计的合理性。
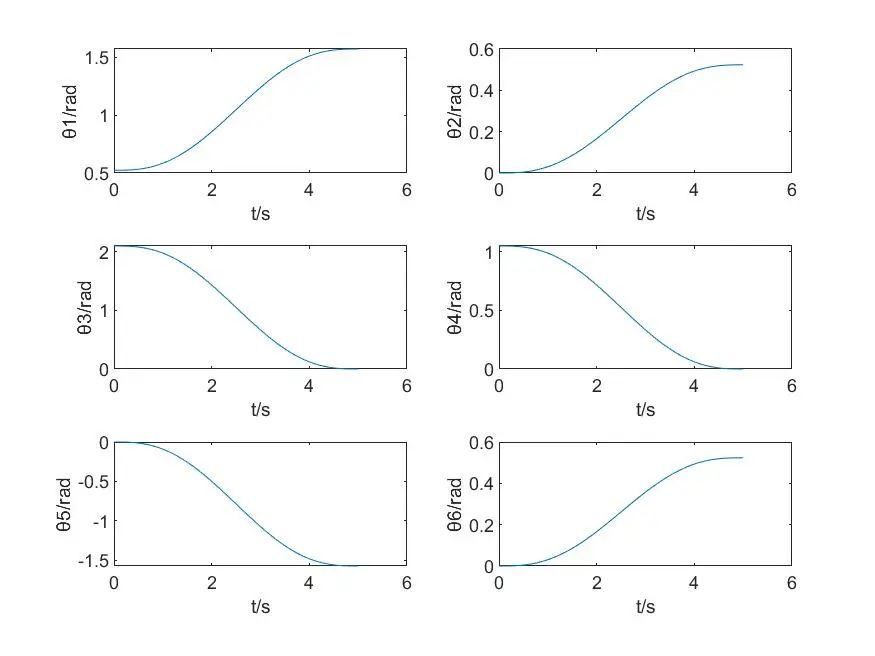
  2. 随着运动的进行， 各个关节的角度与时间关系的曲线， 可以看到其运动过程连续平滑。而且在图 中可以看出各关节的角速度和角加速度都是光滑变化的，没有出现跳变点。进一步地，在首末两点的速度以及加速度都可以有效地约束为零。 
  3. 由此可知，机械臂在进行实际作业时，各关节、 运动部件可以平稳地运行。

 

注：本文部分内容参考：https://mp.weixin.qq.com/s/CQi9wTaje8PmIRXKlrTdBA

 

posted on 2023-09-20 20:58  tdyizhen1314  阅读(3369)  评论(0)  编辑  收藏  举报

导航