(笔记)电流趋肤效应原理

 

趋肤效应的原因非常简单：电流总是沿着阻抗低的方向分布。好比一条河流，沿着河流正中间有一大块石头，那么原本需要从中间流过的一部分水就会被挤到了旁边。

我们首先需要明确一点，如果考虑单独的一个导体：其阻抗并非只有导体的电阻，而是由电阻，感抗构成的；

——“容抗”需要由两个不短路的导体才能构成，“趋肤效应”中跟“容抗”关系不大，先不考虑。

 

那么如何来理解这个事情？咱们分两个情况来看：

一. 直流电流为什么没有趋肤效应？

那是因为直流电流条件下，理想均匀导体各各处（导体横截面的各位置）的阻抗是一样的；

理想导体的阻抗有两部分组成：1，电阻：R；2，感抗（电感）：jωL。所以在直流电流条件下ω = 0，则感抗为0，所以导线的阻抗Z = R；而作为理想均匀导体，其各处的阻抗是相等的，所以电流也是均匀的。

 

二. 交流电流的趋肤效应是怎么回事？

再直接理解趋肤效应之前，需要先了解导体的“自感”是什么？

1，导体的自感

我们所熟知的电感是如下图所示的那样，有一个个的圈圈绕着一个磁芯，然后就成为了一个电感器。

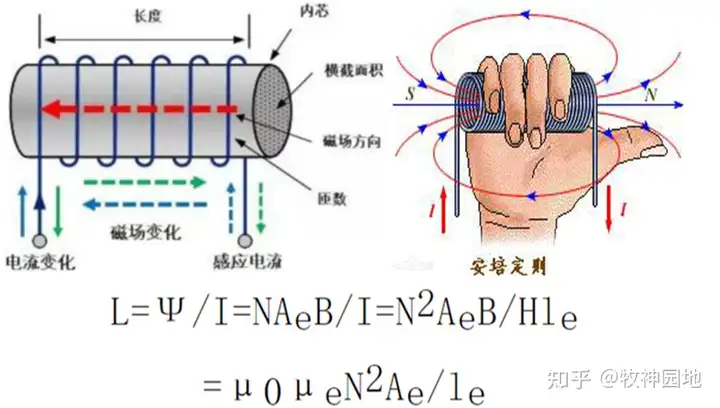
那么如果单独一个笔直的导线（导体），是否存在电感呢？

假设世界上存在这么一段导线，只有这一段有电流，前后都没电流，也没有回流（这种情况实际不存在），那么它有电感么？我们比照电感的定义：当这段导线通过1A电流时，周围是否产生了磁力线？我保证它肯定有，因为只要有电流流过，就会产生围绕着电流的闭合磁力线，差别只在于磁力线匝数的不同（没有那么多圈圈来叠加）。那么，这段导线的电感，我们就称它为：局部自感。

——圆杆导线局部自感近似公式：L = 5*Len[ln(2*Len/r)-(3/4)]。

 

那么导线（导体）上的电感（包括自感）有什么作用？

对导线自身来说，当周围磁力线匝数发生变化时导体两端会产生感应电动势：V = ΔN/Δt = L*ΔI/Δt = L*dI/dt。导线自身电流变化时，它通过自感产生自感电动势，阻止导线自身电流的变化；

——从原理来说，相当于一个电感器的作用，会阻止导线中电流的变化。

当导线中通过直流电流时，导线中的电流分布是均匀的，计算的磁力线匝数重点关注导线外的磁力线，事实上如下左图金箍棒的横截面所示导线内部也存在磁力线，是导线自感的一部分；导线内部和外部磁力线圈都会影响自感，我们称它们为：内部自感和外部自感。

 

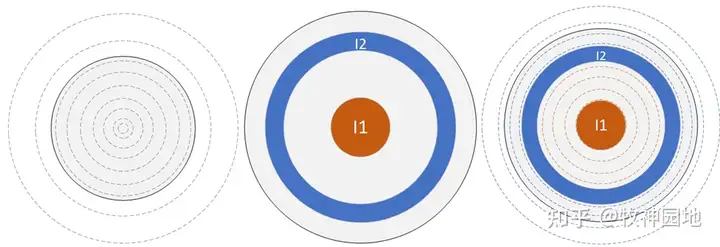
如下中图所示当电流聚集在金箍棒的中间I1或则分散在边缘I2（I1 = I2），它们的自感一样么？

如下右图所示，I1和I2的磁力线只是分别围绕在I1和I2的外面，I1和I2电流大小相等，那么在I2圈外呈现的I1和I2的磁力线匝数（外部电感部分）相同；但是在导线内部I1存在着相比于I2更多的磁力线匝数（内部自感部分），这些多出来的磁力线匝数就是I1相对于I2更大的电感量。

如下图所示为电流在导线内部和外部的磁场强度，导线内部的磁场产生内部自感，而导线外部的磁场产生外部自感；外部自感比内部自感大得多，因此传输线每单位长度电感近似于外部自感。

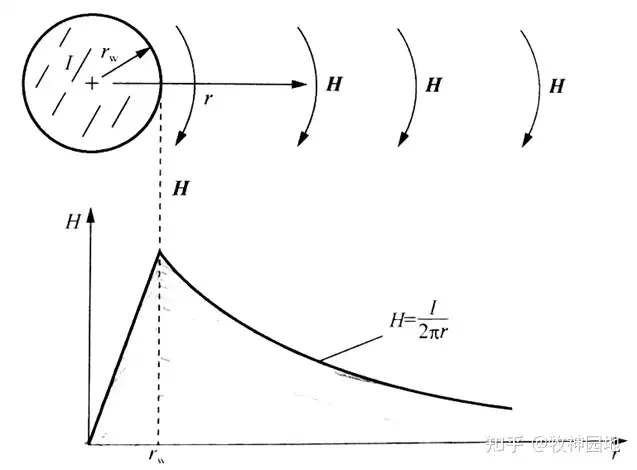
我们知道了圆导线（当然也包括扁导线）的电感为内部自感和外部自感之和，其内部自感是会变化的。

 

2，趋肤效应

我们知道了导线外部的磁力线匝数（外部电感）并不会随着频率的变化而变化，但是导线内部磁力线匝数（内部电感）会随着电流的分布而出现变化。随着频率的增加导线的感抗Z=jωL也随之增加，而电流总是循着最小阻抗的路径流动，当导线感抗与电阻比值随着频率越高越大时，电流便越趋于沿着导线的外表面流动（此时导线内部电感小，减小感抗），这就是趋肤效应。

趋肤效应影响的结果是随信号频率的增大而导线电流趋于分布到导体外表面，影响如下：

1. 导线自感减小，从而减小了传输线的回路电感；

2. 导线电流通过的横截面减小（Z=ρ*L/A），导线电阻增加，线路损耗增加。

 

如果上面的说法太数学，那么我们换一个角度再来感性理解一遍趋肤效应：

我们看到下图中铜棒的磁力线分布，越靠近中心的位置外围所环绕的磁力线越多，说明越靠近铜棒中心的电感值越大，即：越靠近中心所受到的感抗也越大；所以当信号频率增加，根据Z=jωL，随着频率增加电感感抗大于导线电阻值时，电流自然要趋于从更低的阻抗路径通过，即从铜棒的外表层流过。

——电流似乎是个先知，它总能自动的找到阻抗最小的路径，然后选择这条路径通过；这就是电流的自然法则。

 

我们知道了随着电流频率的增加，电流流向导线的外边缘，大部分电流集中在一个厚度等于趋肤深度导线的趋肤深度δ的环面中： δ = δ= √(1/σ*π*μ*f)。其中，σ：电导率；μ：磁导率；f：正弦波频率；一般典型的导体都是非铁磁性的，所以μ = μ0 = 4π* 10−7 。

——铜线的趋肤深度：δ = 66*√(1/f)μm。

如下图所示，趋肤效应会将电流聚集到导线表面，使得通过导线的实际横截面积减小，那么其必然会增加导线的电阻率（单位长度的电阻大小）。如下图所示，对圆导线的电阻损耗进行分析：

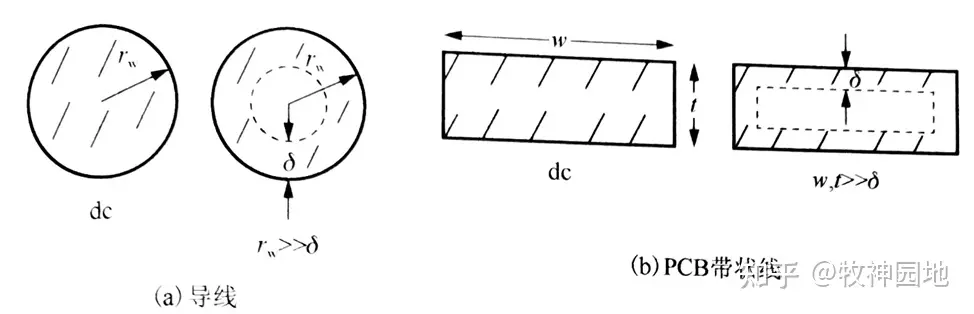
1. 对于直流电流来说，电流均匀分布在导线中，对于左上图的圆导线来说，其单位长度的直流电阻为：rdc =1/(σ*π*rω²)；其中rω表示导线的半径；

——整个圆导线截面上都有电流，横截面积为π*rω²。

2. 随着频率的增加，当趋肤深度小于导体半径：rω >> δ时。单位长度的电阻为rhf = 1/{σ*[π*rω²-π*(rω²-δ)²]} ≈ 1/(σ*2π*rω* δ)；

——圆导线中心（rω - δ）没有电流通过，只有导线外层的一个环（δ）中有电流流过。

3. 根据趋肤深度公式，圆导线δ与频率的平方根成反比，所以根据电阻公式（与趋肤深度成反比）随着频率的增加，单位长度电阻与频率的平方根成正比，即以10dB/10倍频的速度增加，导线单位长度电阻与频率响应曲线如下图所示。

4. 对于右上图中的带状线来说，其直流电阻rdc = 1/(σ*ω*t)；其中ω和t分别是带状线的宽度和厚度；

5. 随着频率的增加，电流趋于集中在带状线厚度等于一个趋肤深度δ的表面，单位长度电阻rhf = 1/[σ*(2δ*t+2δ*δ)] = 1/[2δ*σ*(t+ω)]；此外带状线的高频电阻与频率的平方根成正比，其直流电阻和高频电阻的渐近线频率fbreak处相交。

 

三、写在最后

我们从这个问题中得到的最重要的信息是：电流在有些方面就像水流一样，其总是向阻力最小的方向去分布。这对理解传输线的回流路径分布（领近效应），接地设计，电磁兼容性屏蔽等等概念非常非常重要（相关知识会在个人主页“专栏”中持续持续更新）。