(笔记)运算放大器经典应用电路及工作原理
一、运算放大器(简称运放)
英文全称是Operation Amplifier,简写为OP AMP。顾名思义,运算放大器的初衷是用于执行数学计算,比如加、减、乘、除、函数运算等。在当前的技术条件下,运算放大器的数学运算功能已不再突出,现在主要应用于信号放大及有源滤波器设计。
在多数的常规设计中,我们使用运放的理想模型,忽略其内部结构。把它当作一个“具有放大作用的元件”,接上电源,便可以让它发挥放大的作用。所谓理想的运放,它的输入阻抗无穷大,输出阻抗为零,如图2.1。
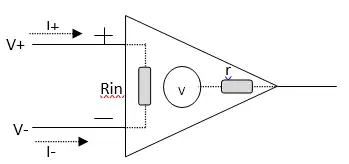
图2.1 运算放大器模型
理想的运放电路分析有两大重要原则贯穿始终,即“虚短”与“虚断”。“虚短”的意思是正端和负端接近短路,即V+=V-,看起来像“短路”;“虚断”的意思是流入正端及负端的电流接近于零,即I+=I-=0,看起来像断路(因为输入阻抗无穷大)。
二、运放的典型应用
1、反相比例放大电路
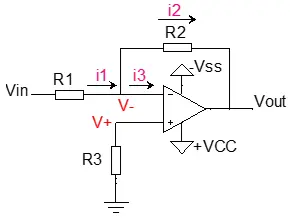
图2.2 比例放大电路
图2.2是典型的比例放大电路,根据“虚短”及“虚断”法则可以很简单的计算得到结果:

等式2.1中负号,代表输出和输入相位相差180°。
推导过程:
(1)、电流的流入等于流出,所以i1=i2+13。由“虚断”法则得知i3=0A,所以i1=i2。
因此,根据第一章介绍的“叠加法则”,得到:
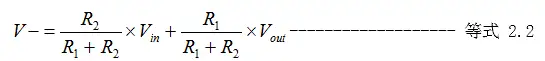
(2)、又根据“虚短”法则,得知运放的正负两个端等同于“短路”,所以V+=V-。而因为运放的正端子V+被R3下拉至地平面,所以V-=V+=0V,代入等式2.2可得到:
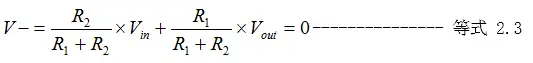
再由等式2.3,进一步得到公式2.1,
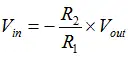
因为Vout与Vin成线性的比例关系,因此这个典型放大电路被称为比例放大电路。
关于R1,R2及R3的选值:
1)、R1,R2及R3应该在K级,不宜达到M级;
2)、R3应该等于或近似于R1与R2的并联,以消除偏置电流的影响。
2、差分放大电路
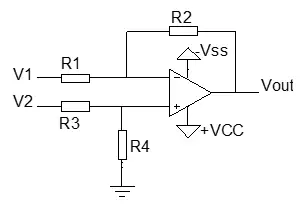
图2.3 差分放大电路
图2.3为差分放大电路,它是图2.2反相比例放大电路的“变种”。类似与反相比例放大电路的分析方法,可以得到结论:
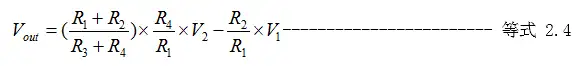
当R1=R3并且R2=R4时,得到等式2.5。这就是此电路命名的由来,它可以对差分信号进行放大。

上文介绍的放大电路会引起相位翻转180°,图2.4为同相放大电路,顾名思义,输出和输入保持相同的相位。理想的运放具有输入阻抗无穷大,输出阻抗无穷小的特点,同相放大电路保持了运放的这种特性。
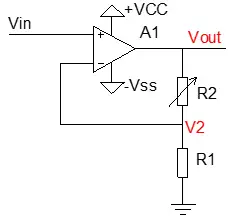
图2.4 同相放大电路
分析图2.4,应用运放的“虚短”,可知V2=V1;此外,因为运放的“虚断”,输出电压的电流全部流经R2和R1,因此V2由R1和R2对Vout分压得到。

因此,

调节R2可以电路的放大倍数。
注意:同相放大电路的应用场合具有局限性,一般只用于直流电平的放大,不适合用于交流信号的放大,因为它会将交流信号的直流偏置电压一并放大,从而使其偏置电位发生偏移。带参考电平的反相比例放大电路在信号放大时比较有实用性。
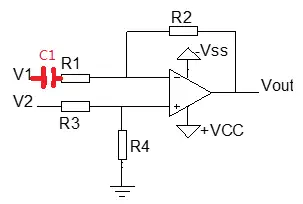
如果需要进行交流信号放大,实际上只是在图2.3的差分放大器的基础上加一个隔直电容C1。
4、电压跟随电路
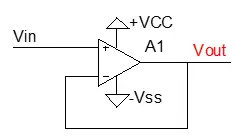
图2.5 电压跟随电路
图2.5是运放的一种特殊应用方式,很容易得到结论Vout=Vin。输出电压跟随输入电压,因此称之为“电压跟随器”。
电压跟随电路是图2.4同相放大电路的衍生产物,是放大倍数为1的同相放大电路。前文已介绍理想的同相放大电路的输入阻抗无穷大,输出阻抗无穷小。
基于此特性,电压跟随电路一般用于信号的隔离。简单举例说明,如图2.6,由R1和R2产生参考电压供给下一级电路使用,因为下一级电路的等效内阻会影响R1和R2的分压比,因此参考电压将会发生变化,如果内阻不是固定的,则此电路将无法使用。
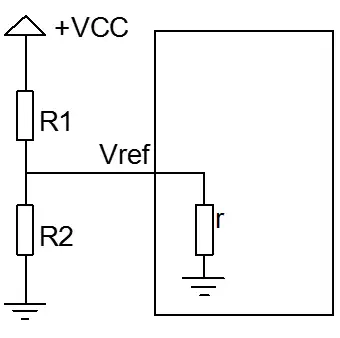
图2.6 不可靠的参考电压电路
比较可靠的设计如图2.7所示:
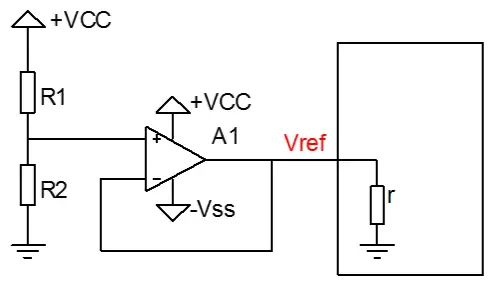
图2.7 可靠的参考电压电路
5、仪器放大电路
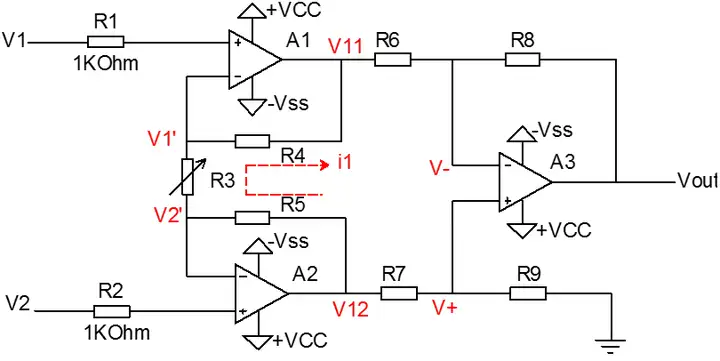
图2.8 仪器放大电路
图2.8是典型的仪器放大电路,顾名思义此方法电路使用于小信号的放大,一般用于传感器信号的放大。传感器的输出信号很小,一般只有几毫伏到几十毫伏。
电路由两级放大电路组成,第一级由A1,A2组成,同相输入,输入阻抗高,电路结构对称,可很好的抑制零点漂移;第二级由A3组成,良好的共模抑制比,输入阻抗高,增益在大范围内可调。
选值要求:R4=R5,R6=R7,R8=R9(保持电路的对称性),R3为可调电阻,用于调节电路增益。电路输入输出的关系式如下:
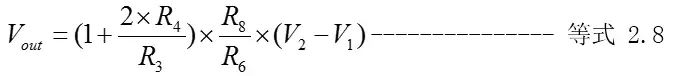
推导过程:
实际上,仪器放大电路是前文所述的同相放大电路及差分放大电路的综合体。分析方法可以参考前文的阐述。
(1)、首先分析由A1和A2组成的同相放大电路。
由“虚短”及“虚断”原则,推导得到:
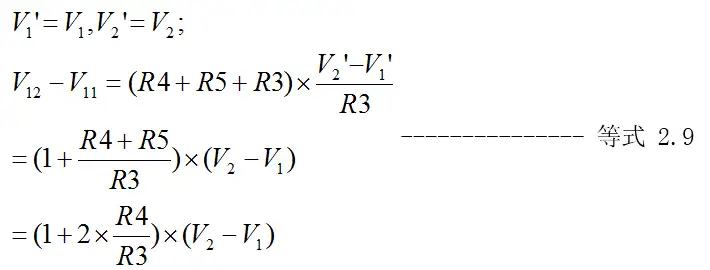
(2)、进一步分析由A3组成的差分放大电路。
由“虚短”及“虚断”原则,推导得到:
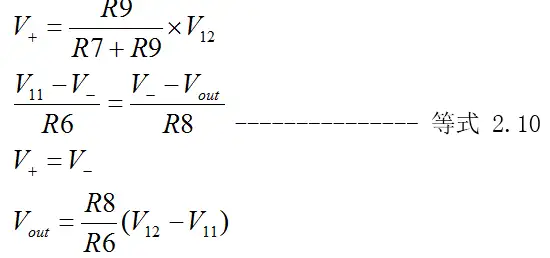
(3)、联合等式2.9和2.10得到结论:
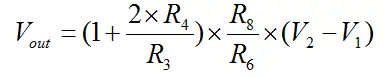
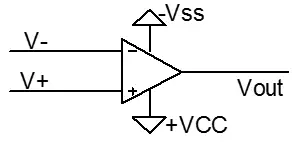
图2.9 简单的比较器
图2.9是最简单的比较器电路,它利用的原理是“理想的运放具有无穷大的增益”。因此,V+与V-之间稍有电压差,即可引起输出的翻转。微弱的电压差经运放放大引起输出饱和。
Av为运放的开环放大倍数(一般为100dB左右,即十万倍)。当V+大于V-时,输出为正饱和(接近VCC,但是无法达到);当V-大于V+时,输出为负饱和(接近-VSS,但是无法达到)。连接V+至地,构成过零比较器,如图2.10所示。
8、过零比较器
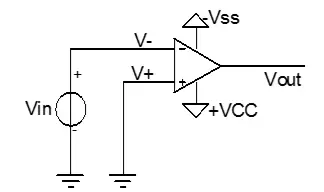
图2.10 过零比较器
图2.10的过零比较器虽然简单,但是并不实用,它的问题在于比较器只有一个临界电压,输入信号上的杂波易引起输出误操作,如图2.11所示。
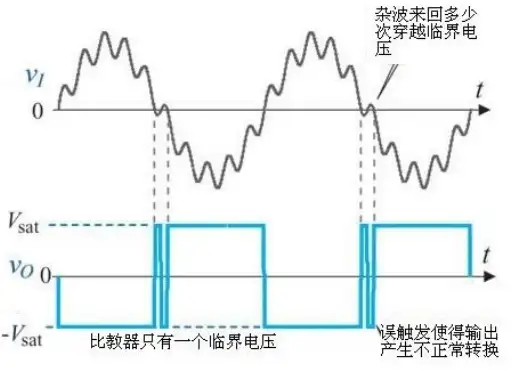
图2.11,信号杂波引起的比较器误操作
9、迟滞比较器(The hysteresis comparator)
相对于上文所述的简单比较器,比较实用的是迟滞比较器,如图2.12所示。
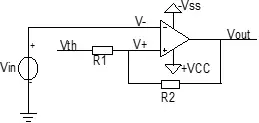
图2.12,迟滞比较器
相比简单比较器,迟滞比较器只是增加了一个电阻R2。这将引起怎样的微妙变化呢?
通俗地说,R2在输入与输出之间搭起了一座桥梁,输出的变化可以通过R2传递至输入,然后比较器的阈值将随输出的变化而改变,达到了迟滞的目的。
如果需要定量分析,所有的比较器的原理都是一样的,利用运放的放大倍速为“无穷大”,将V+与V-之间的微弱电压差进行放大,达到饱和输出。所以,首先计算比较器的临界电压值(V+),得到等式2.11。
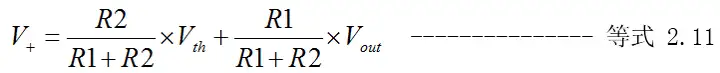
显然,R2的作用是将输出电压引入临界电压。因为Vout会有两种状态+Vsat和-Vsat,所以迟滞比较器也将有两个临界电压(Vth_H及Vth_L)。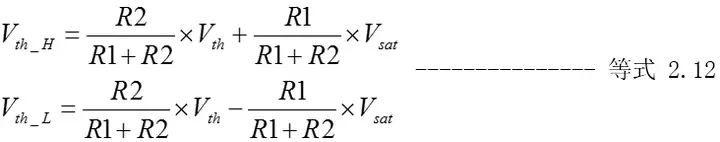
| Vin | 输出电压Vout | 备注 |
| >Vth_H | -Vsat | 此时临界电压变为Vth_L |
| <Vth_L | +Vsat | 此时临界电压变为Vth_H |
| Vth_L <=Vin<=Vth_H | 保持上一个状态 | 保持上一个状态,避免杂波引起的误操作 |
表格2.1,迟滞比较器的状态表
表格2.1可以很好的解释迟滞比较器的工作原理,图2.8是另一种有效的表达迟滞比较器工作原理的方式。设计合适的Vth_H及Vth_L,使(Vth_H-Vth_L)大于杂波幅值,可以有效的避免因为输入信号上的杂波引起的误操作。
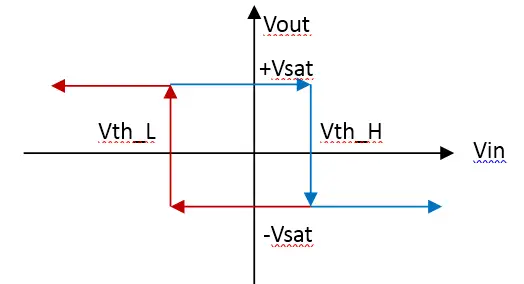
图2.13,迟滞比较器的状态矢量图
10、窗口比较器
窗口比较器用于判别输入电压是否落在某一个范围之内,图2.14是典型的窗口比较器。
其中,URH>URL,D1和D2不能省略,防止两个运放输出电平相反时损坏运放。比如,运放A1输出VOH,但是运放A2输出VOL,D1导通,但是D2截止,因此电流不会从A1流入A2,避免大电流损坏器件。
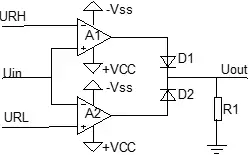
图2.14,窗口比较器
窗口比较的工作原理如图2.15所示。
| Vin | Vout | 备注 |
| Uin>URH>URL | UOH | A1输出UOH,A2输出UOL,D1导通,D2截止 |
| Uin<URL<URH | UOH | A1输出UOL,A2输出UOH,D1截止,D2导通 |
| URL< Uin<URH | UOL | A1输出UOL,A2输出UOL,D1截止,D2截止 |
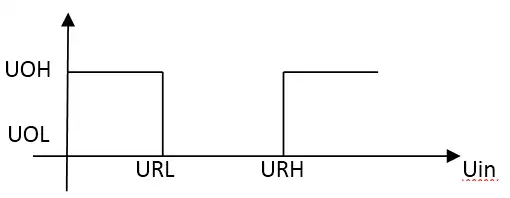
图2.15,窗口比较器的逻辑
11、同相加法器
举个栗子:Vin1=0.4*Sin(wt) 也就是一个正弦信号 Vin2=1V 那么要实现两个信号的叠加而且相位不发生变化:也就是Vout=1+0.4Sin(wt) ;那么就可以使用同相加法器。
也就是需要实现如下过程:

原理图如下图所示:

Vout与输入的关系如下:

当R1=R2,R3=R4时,即可实现:Vout=Vin1+Vin2
12、反相加法器

Vout与输入的关系如下:

当R1=R2,R3=R4时,即可实现:Vout=-(Vin1+Vin2)
13、减法器

Uo与输入的关系如下:

当R1=R2,R3=Rf时,即可实现:Uo=-(RF/R1)(Ui2-Ui1)
14、积分运算电路



从该公式可以看出,输出信号与输入信号成比例,比例系数为负值,即在t>0的区别内,输出信号是一个逐渐减小的量,但他不会一直无限制的减小,但输出信号≤负的饱和输出电压时,就会保持该电压值不变了。
15、微分运算电路



由图可知,在输入信号的上升沿和下降沿,输出端有尖脉冲波形,尖脉冲波形的宽度与时间常数 (RfCf) 有关,时间常数越小,尖脉冲波形越尖,反之则越宽。
此外,尖脉冲的最大值受集成运放饱和输出电压的限制。
从输入输出波形可以看出,微分运算电路可以将矩形脉冲波转换为尖形脉冲波,当微分电路用作信号转换电路时,特别需要注意的是时间常数 (RfCf) ,必须小于输入脉冲的宽度,否则会失去波形变化的作用。一般时间常数 (RfCf) 应该 ≤1/10 输入脉冲宽度。
posted on 2023-01-28 14:59 tdyizhen1314 阅读(14665) 评论(0) 编辑 收藏 举报




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 在鹅厂做java开发是什么体验
· 百万级群聊的设计实践
· WPF到Web的无缝过渡:英雄联盟客户端的OpenSilver迁移实战
· 永远不要相信用户的输入:从 SQL 注入攻防看输入验证的重要性
· 全网最简单!3分钟用满血DeepSeek R1开发一款AI智能客服,零代码轻松接入微信、公众号、小程