(笔记)PID算法讲解（原理+算法+源码）

 

 

 

PID算法资料很多，质量高低不一，但若想把PID研究透，还是需要仔细甄别与筛选。本文根据网上一些较好的文章及个人理解，整理成文，也是给自己做了笔记。

在此感谢： https://zhuanlan.zhihu.com/p/16875161

 

注：由于博客园没法直接附上文件，若需要算法源码及可运行文件（已在uBuntu上验证），可以留言邮箱，我会通过邮件给到。

 

1 前言

控制系统通常根据有没有反馈会分为开环系统和闭环系统，在闭环系统的控制中，PID算法非常强大，其三个部分分别为；

• P：比例环节；
• I：积分环节；
• D：微分环节；

PID算法可以自动对控制系统进行准确且迅速的校正，因此被广泛地应用于工业控制系统。

 

2 开环控制

首先来看开环控制系统，如下图所示，隆哥蒙着眼，需要走到虚线旗帜所表示的目标位置，由于缺少反馈（眼睛可以感知当前距离和位置，由于眼睛被蒙上没有反馈，所以这也是一个开环系统），最终隆哥会较大概率偏离预期的目标，可能会运行到途中实线旗帜所表示的位置。

开环系统的整体结构如下所示；

 

这里做一个不是很恰当的比喻；

• Input：        告诉隆哥目标距离的直线位置（10米）；
• Controller：隆哥大脑中计算出到达目标所需要走多少步；
• Process：     双腿作为执行机构，输出了相应的步数，但是最终仍然偏离了目标；

      看来没有反馈的存在，很难准确到达目标位置。

 

3 闭环控制

所以为了准确到达目标位置，这里就需要引入反馈，具体如下图所示；

 

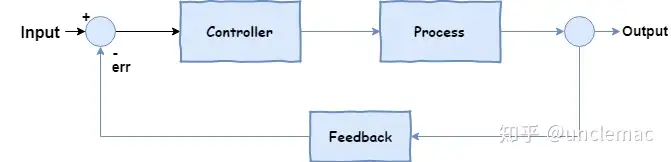
在这里继续举个不怎么恰当的比喻；隆哥重获光明之后，基本可以看到目标位置了；

• 第一步Input：         告诉隆哥目标距离的直线位置（10米）；
• 第二步Controller：隆哥大脑中计算出到达目标所需要走多少步；
• 第三步Process：     双腿作为执行机构，输出了相应的步数，但是最终仍然偏离了目标；
• 第四步Feedback：   通过视觉获取到目前已经前进的距离，（比如前进了2米，那么还有8米的偏差）；
• 第五步err：            根据偏差重新计算所需要的步数，然后重复上述四个步骤，最终隆哥达到最终的目标位置。

 

4 PID

4.1 系统架构

虽然在反馈系统下，隆哥最终到达目标位置，但是现在又来了新的任务，就是又快又准地到达目标位置。所以这里隆哥开始采用PID Controller，只要适当调整P，I和D的参数，就可以到达目标位置，具体如下图所示；

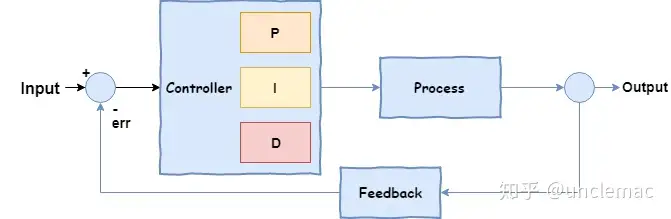
隆哥为了最短时间内到达目标位置，进行了不断的尝试，分别出现了以下几种情况；

• 跑得太快，最终导致冲过了目标位置还得往回跑；
• 跑得太慢，最终导致到达目标位置所用时间太长；

经过不断的尝试，终于找到了最佳的方式，其过程大概如下图所示；

 

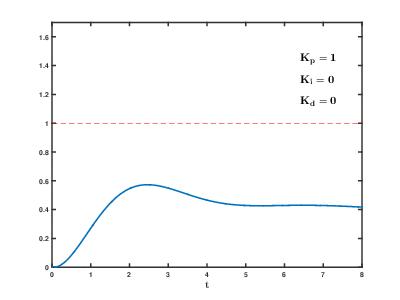
这里依然举一个不是很恰当的比喻；

• 第一步：得到与目标位置的距离偏差（比如最开始是10米，后面会逐渐变小）；
• 第二步：根据误差，预估需要多少速度，如何估算呢，看下面几步；

---

P比例则是给定一个速度的大致范围，满足下面这个公式；

K_p∗e(t)

因此比例作用相当于某一时刻的偏差（err）与比例系数Kp的乘积，具体如下所示；

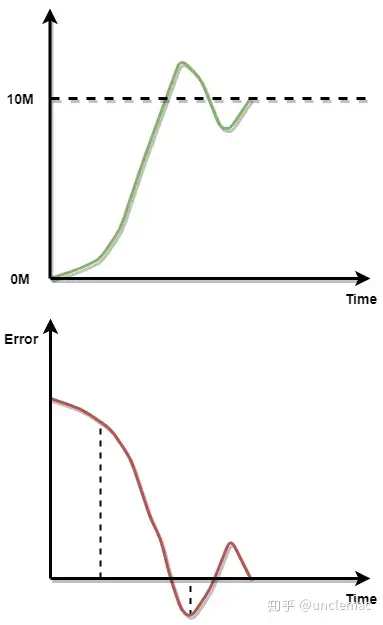
绿色线为上述例子中从初始位置到目标位置的距离变化； 红色线为上述例子中从初始位置到目标位置的偏差变化，两者为互补的关系；

---

I积分则是误差在一定时间内的和，满足以下公式；

K_i∫₀te(_t)d_t

如下图所示；

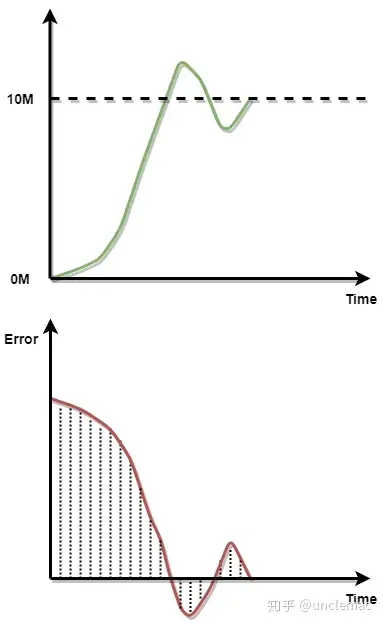
红色曲线阴影部分面积即为积分作用的结果，其不断累积的误差，最终乘以积分系数Ki就得到了积分部分的输出；

 

---

D微分则是误差变化曲线某处的导数，或者说是某一点的斜率，因此这里需要引入微分；

K_dde(t)d_t

 

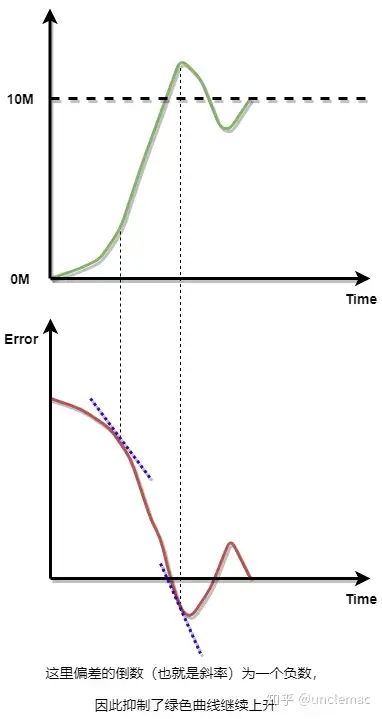
从图中可知，当偏差变化过快，微分环节会输出较大的负数，作为抑制输出继续上升，从而抑制过冲。

 

---

综上，，，K_p，K_i，K_d，分别增加其中一项参数会对系统造成的影响总结如下表所示；

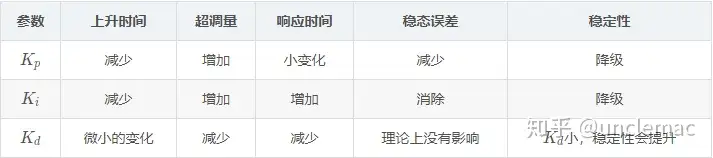
4.2 理论基础

上面讲了这么多，无非是为了初步理解PID在负反馈系统中的调节作用，下面开始推导一下算法实现的具体过程；PID控制器的系统框图如下所示；

 

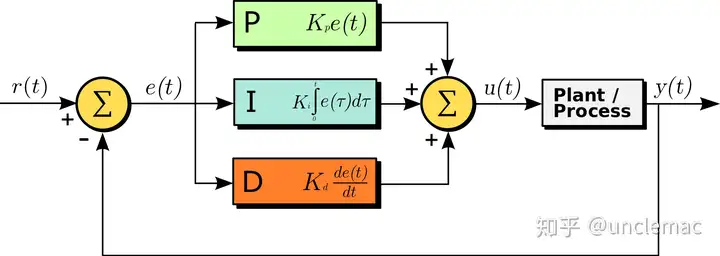
因此不难得出输入e(t)和输出u(t)的关系；

K_p是比例增益； K_i是积分增益； K_d是微分增益；

 

4.3 离散化

在数字系统中进行PID算法控制，需要对上述算法进行离散化；假设系统采样时间为Δt 则将输入e(t)序列化得到；

 

 

 

4.4 伪算法

这里简单总结一下位置式PID实现的伪算法；

previous_error := 0  //上一次偏差
integral := 0            //积分和

//循环 
//采样周期为dt
loop:
   //setpoint 设定值
   //measured_value 反馈值
    error := setpoint − measured_value                                 //计算得到偏差
    integral := integral + error × dt                                  //计算得到积分累加和
    derivative := (error − previous_error) / dt                        //计算得到微分
    output := Kp × error + Ki × integral + Kd × derivative             //计算得到PID输出
    previous_error := error                                            //保存当前偏差为下一次采样时所需要的历史偏差
    wait(dt)                                                           //等待下一次采用
    goto loop

 

对于一些简单的应用，如温控、压力控，dt时间通常可简单地将其置为单位时间1就行，此时公式就更简化了。

 

　　

5 C++实现

 

这里是位置式PID算法的C语言实现；

 

pid.cpp

#ifndef _PID_SOURCE_
#define _PID_SOURCE_

#include <iostream>
#include <cmath>
#include "pid.chh"

using namespace std;

class PIDImpl
{
public:
    PIDImpl(double dt, double max, double min, double Kp, double Kd, double Ki);
    ~PIDImpl();
    double calculate(double setpoint, double pv);

private:
    double _dt;
    double _max;
    double _min;
    double _Kp;
    double _Kd;
    double _Ki;
    double _pre_error;
    double _integral;
};


PID::PID(double dt, double max, double min, double Kp, double Kd, double Ki)
{
    pimpl = new PIDImpl(dt, max, min, Kp, Kd, Ki);
}

double PID::calculate(double setpoint, double pv)
{
    return pimpl->calculate(setpoint, pv);
}

PID::~PID()
{
    delete pimpl;
}


/**
 * Implementation
 */
PIDImpl::PIDImpl(double dt, double max, double min, double Kp, double Kd, double Ki):
    _dt(dt),
    _max(max),
    _min(min),
    _Kp(Kp),
    _Kd(Kd),
    _Ki(Ki),
    _pre_error(0),
    _integral(0)
{
}

double PIDImpl::calculate(double setpoint, double pv)
{
    const float intergral_max_value = 1000;                 //积分限幅值大小,调试时确定

    //计算当前误差
    double cur_error = setpoint - pv;

    //计算比例值
    double Pout = _Kp * cur_error;

    //计算积分值(考虑积分限幅)
    _integral += cur_error * _dt;                           //累计误差
    if (_integral > intergral_max_value)
        _integral = intergral_max_value;
    else if (_integral < -intergral_max_value)
        _integral = -intergral_max_value;
    double Iout = _Ki * _integral;

    //计算微分值
    double derivative = (cur_error - _pre_error) / _dt;
    double Dout = _Kd * derivative;

    //计算PID输出结果
    double output = Pout + Iout + Dout;

    //输出限幅
    if (output > _max)
        output = _max;
    else if (output < _min)
        output = _min;

    //保存当前误差值，该值将作为下一次PID计算的上一次误差值
    _pre_error = cur_error;

    return output;
}

PIDImpl::~PIDImpl()
{
}

#endif

　　

　

 

pid.h

#ifndef _PID_H_
#define _PID_H_

class PIDImpl;
class PID
{
    public:
        // Kp -  proportional gain
        // Ki -  Integral gain
        // Kd -  derivative gain
        // dt -  loop interval time
        // max - maximum value of manipulated variable
        // min - minimum value of manipulated variable
        PID( double dt, double max, double min, double Kp, double Kd, double Ki );

        // Returns the manipulated variable given a setpoint and current process value
        double calculate( double setpoint, double pv );
        ~PID();

    private:
        PIDImpl *pimpl;
};

#endif

　　

 

main.cpp

#include "pid.chh"
#include <stdio.h>

int main()
{
    PID pid = PID(0.1, 100, -100, 0.4, 0.01, 0.5);

    double val = 500;
    for (int i = 0; i < 100; i++)
    {
        double inc = pid.calculate(0, val);
        printf("[%04d] val:% 7.6f inc:% 7.6f\n", i, val, inc);
        val += inc;
    }

    return 0;
}

　　

 

编译并测试：

# To compile example code:
g++ main.cpp pid.cpp -o main
./main

　　

 测试结果如下：（注：PID值的选取非常重要，不同的PID值，逼近目标值所需的计数次数会不同）

dade@ubuntu:~/Desktop/PID$ g++ main.cpp pid.cpp -o main
dade@ubuntu:~/Desktop/PID$ ./main
[0000] val: 500.000000 inc:-100.000000
[0001] val: 400.000000 inc:-100.000000
[0002] val: 300.000000 inc:-100.000000
[0003] val: 200.000000 inc:-100.000000
[0004] val: 100.000000 inc:-100.000000
[0005] val: 0.000000 inc:-65.000000
[0006] val:-65.000000 inc:-39.250000
[0007] val:-104.250000 inc:-20.912500
[0008] val:-125.162500 inc:-8.123125
[0009] val:-133.285625 inc: 0.511469
[0010] val:-132.774156 inc: 6.082130
[0011] val:-126.692027 inc: 9.426813
[0012] val:-117.265214 inc: 11.184880
[0013] val:-106.080333 inc: 11.839138
[0014] val:-94.241195 inc: 11.750117
[0015] val:-82.491078 inc: 11.183526
[0016] val:-71.307552 inc: 10.332152
[0017] val:-60.975400 inc: 9.333199
[0018] val:-51.642201 inc: 8.281925
[0019] val:-43.360276 inc: 7.242296
[0020] val:-36.117980 inc: 6.255240
[0021] val:-29.862741 inc: 5.344986
[0022] val:-24.517755 inc: 4.523905
[0023] val:-19.993850 inc: 3.796144
[0024] val:-16.197706 inc: 3.160348
[0025] val:-13.037358 inc: 2.611656
[0026] val:-10.425702 inc: 2.143148
[0027] val:-8.282555 inc: 1.746867
[0028] val:-6.535687 inc: 1.414533
[0029] val:-5.121154 inc: 1.138011
[0030] val:-3.983144 inc: 0.909616
[0031] val:-3.073528 inc: 0.722285
[0032] val:-2.351242 inc: 0.569666
[0033] val:-1.781576 inc: 0.446141
[0034] val:-1.335435 inc: 0.346809
[0035] val:-0.988627 inc: 0.267450
[0036] val:-0.721177 inc: 0.204465
[0037] val:-0.516712 inc: 0.154813
[0038] val:-0.361899 inc: 0.115948
[0039] val:-0.245952 inc: 0.085753
[0040] val:-0.160199 inc: 0.062481
[0041] val:-0.097718 inc: 0.044702
[0042] val:-0.053016 inc: 0.031250
[0043] val:-0.021766 inc: 0.021183
[0044] val:-0.000583 inc: 0.013746
[0045] val: 0.013163 inc: 0.008333
[0046] val: 0.021496 inc: 0.004466
[0047] val: 0.025962 inc: 0.001768
[0048] val: 0.027731 inc:-0.000056
[0049] val: 0.027675 inc:-0.001235
[0050] val: 0.026440 inc:-0.001945
[0051] val: 0.024495 inc:-0.002321
[0052] val: 0.022175 inc:-0.002464
[0053] val: 0.019711 inc:-0.002449
[0054] val: 0.017262 inc:-0.002334
[0055] val: 0.014927 inc:-0.002158
[0056] val: 0.012769 inc:-0.001951
[0057] val: 0.010818 inc:-0.001732
[0058] val: 0.009086 inc:-0.001516
[0059] val: 0.007570 inc:-0.001309
[0060] val: 0.006261 inc:-0.001119
[0061] val: 0.005141 inc:-0.000948
[0062] val: 0.004194 inc:-0.000795
[0063] val: 0.003398 inc:-0.000662
[0064] val: 0.002736 inc:-0.000548
[0065] val: 0.002188 inc:-0.000449
[0066] val: 0.001739 inc:-0.000366
[0067] val: 0.001372 inc:-0.000297
[0068] val: 0.001076 inc:-0.000239
[0069] val: 0.000837 inc:-0.000191
[0070] val: 0.000646 inc:-0.000152
[0071] val: 0.000494 inc:-0.000120
[0072] val: 0.000375 inc:-0.000094
[0073] val: 0.000281 inc:-0.000073
[0074] val: 0.000208 inc:-0.000056
[0075] val: 0.000152 inc:-0.000043
[0076] val: 0.000109 inc:-0.000033
[0077] val: 0.000076 inc:-0.000024
[0078] val: 0.000052 inc:-0.000018
[0079] val: 0.000034 inc:-0.000013
[0080] val: 0.000021 inc:-0.000009
[0081] val: 0.000011 inc:-0.000007
[0082] val: 0.000005 inc:-0.000004
[0083] val: 0.000000 inc:-0.000003
[0084] val:-0.000003 inc:-0.000002
[0085] val:-0.000004 inc:-0.000001
[0086] val:-0.000005 inc:-0.000000
[0087] val:-0.000006 inc: 0.000000
[0088] val:-0.000006 inc: 0.000000
[0089] val:-0.000006 inc: 0.000000
[0090] val:-0.000005 inc: 0.000000
[0091] val:-0.000005 inc: 0.000001
[0092] val:-0.000004 inc: 0.000001
[0093] val:-0.000004 inc: 0.000000
[0094] val:-0.000003 inc: 0.000000
[0095] val:-0.000003 inc: 0.000000
[0096] val:-0.000002 inc: 0.000000
[0097] val:-0.000002 inc: 0.000000
[0098] val:-0.000002 inc: 0.000000
[0099] val:-0.000001 inc: 0.000000