(笔记)（5）AMCL包源码分析 | 粒子滤波器模型与pf文件夹(一)
粒子滤波器这部分内容涉及到的理论和数据结构比较多，我们分好几讲来介绍。这一讲的内容是对pf文件夹的简要分析，蒙特卡罗定位在pf中的代码具体实现，KLD采样算法的理论介绍以及它在pf中的代码具体实现。
1.pf文件夹头文件简要分析
说到AMCL包下的pf文件夹，它其实就是 由这几部分组成：一个3✖3对称矩阵的特征值和特征向量的分解，定义一个kdtree以及维护方法来管理所有的粒子(粒子在这里表征位姿和权重)，给定Gaussian模型以及概率密度模型采样生成粒子，定义三维列向量，三维矩阵以及实现pose的向量的加减乘除，局部到全局坐标的转换以及全局坐标到局部坐标的转换。
图1.AMCL包pf文件夹展开
接下来，是各个头文件的简要分析。
图2.pf包头文件简要分析
2.粒子滤波器与蒙特卡罗定位
2.1 蒙特卡罗定位算法
什么是粒子滤波器呢？AMCL定位的理论基础就是基于滤波方法，是属于粒子滤波的一种。关于粒子滤波的原理以及代码效果演示，可以转到这里查阅一下。
2.2改进的蒙特卡洛算法：Augmented_MCL算法
那么在这里，AMCL包里的粒子滤波器究竟如何起作用呢？先贴出这个：
图3.AMCL粒子滤波器的算法原理
关于sample_motion_model代码实现，来源于pf.cpp的pf_update_action函数：
// Update the filter with some new action
void pf_update_action(pf_t *pf, pf_action_model_fn_t action_fn, void *action_data)
{
pf_sample_set_t *set;
set = pf->sets + pf->current_set;
(*action_fn) (action_data, set);
return;
}关于measurement_model的代码实现，来源于pf.cpp的pf_update_sensor函数：
// Update the filter with some new sensor observation
void pf_update_sensor(pf_t *pf, pf_sensor_model_fn_t sensor_fn, void *sensor_data)
{
int i;
pf_sample_set_t *set;
pf_sample_t *sample;
double total;
set = pf->sets + pf->current_set;
// Compute the sample weights
total = (*sensor_fn) (sensor_data, set);
/*2021-08-13:Limingxia add:*/
//get score by cabin
match_score_= total;
set->n_effective = 0;
if (total > 0.0)
{
// Normalize weights
double w_avg=0.0;
for (i = 0; i < set->sample_count; i++)
{
sample = set->samples + i;
w_avg += sample->weight;
sample->weight /= total;
set->n_effective += sample->weight*sample->weight;
}
// Update running averages of likelihood of samples (Prob Rob p258)
w_avg /= set->sample_count;
if(pf->w_slow == 0.0)
pf->w_slow = w_avg;
else
pf->w_slow += pf->alpha_slow * (w_avg - pf->w_slow);
if(pf->w_fast == 0.0)
pf->w_fast = w_avg;
else
pf->w_fast += pf->alpha_fast * (w_avg - pf->w_fast);
//printf("w_avg: %e slow: %e fast: %e\n",
//w_avg, pf->w_slow, pf->w_fast);
}
else
{
// Handle zero total
for (i = 0; i < set->sample_count; i++)
{
sample = set->samples + i;
sample->weight = 1.0 / set->sample_count;
}
}
set->n_effective = 1.0/set->n_effective;
return;
}3.AMCL：引入KLD采样理论对蒙特卡罗定位进行再次改进的结果
参考自《概率机器人》第8章 移动机器人定位:栅格与蒙特卡罗。关于第8章的详细阐述可以参考该博主的链接：
以下内容摘自《概率机器人》第8章：
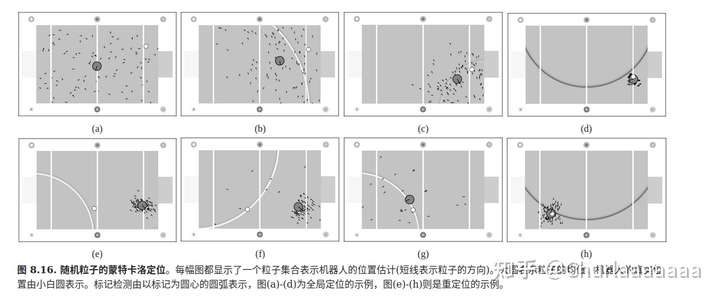
“对于粒子滤波器的效率来说，用于表示置信度的采样集的大小是一个重要的参数。到目前为止，仅讨论了使用固定大小样本集合的粒子滤波。不幸的是，为了避免由于蒙特卡罗定位采样消耗引起的发散，必须选择大样本集合，以便使移动机器人能够处理全局定位和位置跟踪问题。计算资源的浪费。在这个示例中，所有样本集合都包含10000个粒子。尽管在定位的早期阶段这样高的粒子数可能是精确表示置信度所必需的。但是一旦知道机器人在哪里，仅需要一小部分粒子就足以跟踪机器人的位置。
KLD:全称为Kullback-Leibler Divergence,中文名为 库尔贝克-莱布勒散度。KLD采样是蒙特卡罗定位的一个变种，它能随时间改变粒子数。本书不介绍KLD采样的数学推导，只给出算法及一些实验结果。KLD是指两个概率分布差的测度。KLD采样的思想基础是基于采样的近似质量的统计界限来确定粒子数。具体来说，对于每次粒子滤波迭代，KLD采样以概率1-sigma确定样本数，使得真实的后验与基于采样的近似之间的误差小于err。
在几种假设条件下，可以得到利用该方法的有效实现，不过这几种假设条件这里先不做介绍。
3.1 KLD_Sampling_MCL算法介绍
图3 KLD采样算法
程序8.4给出了KLD采样算法。算法把以前的采样集合，地图和最新的控制及测量作为输入。与蒙特卡罗定位形成鲜明对照的是，KLD采样把一个加权后采样集合作为输入。就是说X（t-1）中的样本不是重采样。另外，算法要求统计误差界限err和sigma。
总之，在满足第16行的统计界限之前，KLD采样将一直产生粒子。这个界限基于粒子所覆盖的状态空间的“体积”。粒子覆盖的体积由覆盖在三维状态空间的位或栅格来衡量。直方图H的每位要么空着，要么被至少一个粒子占据。最初，每个位设为空。（第4～6行）。在第8行，一个粒子是从以前样本集合取出来的。基于这个粒子，一个新粒子被预测，加权，并且插入到新采样集合 （ 第9～11行，就像蒙特卡洛定位那样）。第12～19行实现了KLD采样的关键思想。如果新产生的粒子落入直方图的一个空位里，那么非空位数目k是增加的，并且该位被标记为非空。因此，k是至少填充了一个粒子的直方图的位数。这个数目在第16行所确定的统计界限里扮演着决定性的角色。数量Mx给出达到这个界限需要的粒子数。
注意，第一，对于给定的err，Mx通常线性于非空位数k;第二，当k增加时，可忽略非线性项。Z（1-sigma）基于参数（sigma）。它代表标准正态分布上的1-sigma分位点。对典型值sigma，Z（1-sigma）的值在标准统计表里是现成的。算法产生新粒子，直到粒子数M超过Mx和使用者定义的最小值Mx（min）。可以看出，阈值Mx是M的活动目标。产生的样本数目M越大，直方图里非空位k越多，并且阈值Mx就越高。
实际上，算法是否终止取决于下面几个原因。在采样早期，由于所有位都是空的，k几乎随着每次新采样而增加。k的增加导致阈值Mx的增加。然而，经过一段时间以后，越来越多的位变为非空，并且Mx只是偶尔增加。由于M随每次新采样增加，M将最终达到Mx，采样停止。究竟什么时候发生这种情况，要根据置信度来确定。粒子越分散，越多的空位被填满，并且阈值Mx就越高。在跟踪过程中，KLD采样产生的样本较少，因为粒子集中在少数的几个位里。应当注意到，直方图本身对粒子分布没有影响，它唯一的作用是衡量置信度的复杂度或体积。栅格在每次粒子滤波迭代的最后被丢弃。使用KLD采样的采样集合的示例结果阐述:
算法在全局定位的初始阶段要选择非常多的样本。一旦机器人被定位，粒子数会下降到较低水平(小于最初粒子数的1%)。从全局定位到位置追踪的转换什么时候发生及速度有多快，依赖环境的类型和传感器的精度。在这个示例里，激光测距仪的较高精度被定位初期向较低(粒子数)水平的转变反映出来。图8.18给出了KLD采样和具有固定采样集合的蒙特卡罗定位的近似误差的比较。
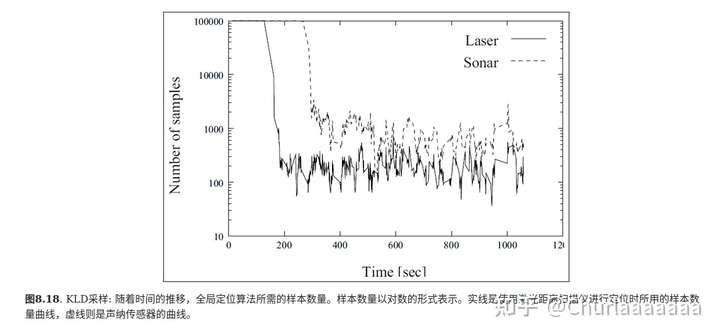
近似误差用根据不同数量的采样生成的置信度(采样集)和“最优“置信度的库尔贝克-莱布勒距离衡量。这些“最优”置信度通过运行蒙特卡罗定位，由大小为200000的样本集产生，其数目远远大于实际位置估计所需要的数目。正如预期的，两种方法使用的样本越多，近似误差就越小。虚线所示为蒙特卡罗定位使用不同大小的采样集合时得到的结果。可以看出，收敛到库尔贝克-莱布勒距离0.25以内，固定方法需要大约50000个样本。较大的误差通常意味着粒子滤波发散，并且不能定位机器人。实线所示为使用KLD采样时的结果。这里采样集合的大小是整个全局定位运行的平均水平。不同数据点是通过在0.4～0.015改变误差界限err得到的，从左到右逐渐降低。平均仅使用3000个样本，KLD采样就能收敛到小误差水平。KLD采样不能保证精确地跟踪最优置信度。由于太宽的误差界限，实线最左边的数据点表明KLD采样发散。
KLD采样能被任意粒子滤波使用，而不仅是蒙特卡罗定位。直方图可以作为固定多维栅格的实现，也可以更简洁地作为树结构（kd tree）的实现。
在机器人定位情境下，KLD采样一直优于具有固定样本集合大小的蒙特卡罗定位。这个技术的优点对全局定位和跟踪相结合的问题意义重大。
实际上，误差界限值1-sigma约为0.99，err约为0.05，直方图位的大小为50cmx50cmx15度，就能取得良好的结果。”
以上就是《概率机器人》第8章关于引用KLD采样的理论阐述了，接下来是KLD采样算法在AMCL包里的具体应用。
3.2 KLD采样算法在AMCL包中的具体应用
代码在pf.cpp中的pf_update_resample函数中实现：
// Resample the distribution
void pf_update_resample(pf_t *pf)
{
int i;
double total;
pf_sample_set_t *set_a, *set_b;
pf_sample_t *sample_a, *sample_b;
//double r,c,U;
//int m;
//double count_inv;
double* c;
double w_diff;
set_a = pf->sets + pf->current_set;
set_b = pf->sets + (pf->current_set + 1) % 2;
if (pf->selective_resampling != 0)
{
if (set_a->n_effective > 0.5*(set_a->sample_count))
{
// copy set a to b
copy_set(set_a,set_b);
// Re-compute cluster statistics
pf_cluster_stats(pf, set_b);
// Use the newly created sample set
pf->current_set = (pf->current_set + 1) % 2;
return;
}
}
// Build up cumulative probability table for resampling.
// TODO: Replace this with a more efficient procedure
// (e.g., http://www.network-theory.co.uk/docs/gslref/GeneralDiscreteDistributions.html)
c = (double*)malloc(sizeof(double)*(set_a->sample_count+1));
c[0] = 0.0;
for(i=0;i<set_a->sample_count;i++)
c[i+1] = c[i]+set_a->samples[i].weight;
// Create the kd tree for adaptive sampling
pf_kdtree_clear(set_b->kdtree);
// Draw samples from set a to create set b.
total = 0;
set_b->sample_count = 0;
w_diff = 1.0 - pf->w_fast / pf->w_slow;
if(w_diff < 0.0)
w_diff = 0.0;
//printf("w_diff: %9.6f\n", w_diff);
// Can't (easily) combine low-variance sampler with KLD adaptive
// sampling, so we'll take the more traditional route.
/*
// Low-variance resampler, taken from Probabilistic Robotics, p110
count_inv = 1.0/set_a->sample_count;
r = drand48() * count_inv;
c = set_a->samples[0].weight;
i = 0;
m = 0;
*/
while(set_b->sample_count < pf->max_samples)
{
sample_b = set_b->samples + set_b->sample_count++;
if(drand48() < w_diff)
sample_b->pose = (pf->random_pose_fn)(pf->random_pose_data);
else
{
// Can't (easily) combine low-variance sampler with KLD adaptive
// sampling, so we'll take the more traditional route.
/*
// Low-variance resampler, taken from Probabilistic Robotics, p110
U = r + m * count_inv;
while(U>c)
{
i++;
// Handle wrap-around by resetting counters and picking a new random
// number
if(i >= set_a->sample_count)
{
r = drand48() * count_inv;
c = set_a->samples[0].weight;
i = 0;
m = 0;
U = r + m * count_inv;
continue;
}
c += set_a->samples[i].weight;
}
m++;
*/
// Naive discrete event sampler
double r;
r = drand48();
for(i=0;i<set_a->sample_count;i++)
{
if((c[i] <= r) && (r < c[i+1]))
break;
}
assert(i<set_a->sample_count);
sample_a = set_a->samples + i;
assert(sample_a->weight > 0);
// Add sample to list
sample_b->pose = sample_a->pose;
}
sample_b->weight = 1.0;
total += sample_b->weight;
// Add sample to histogram(kdtree)
pf_kdtree_insert(set_b->kdtree, sample_b->pose, sample_b->weight);
// See if we have enough samples yet
if (set_b->sample_count > pf_resample_limit(pf, set_b->kdtree->leaf_count))
break;
}
// Reset averages, to avoid spiraling off into complete randomness.
if(w_diff > 0.0)
pf->w_slow = pf->w_fast = 0.0;
//fprintf(stderr, "\n\n");
// Normalize weights
for (i = 0; i < set_b->sample_count; i++)
{
sample_b = set_b->samples + i;
sample_b->weight /= total;
}
// Re-compute cluster statistics
pf_cluster_stats(pf, set_b);
// Use the newly created sample set
pf->current_set = (pf->current_set + 1) % 2;
pf_update_converged(pf);
free(c);
return;
}好了，以上就是关于pf包的相关理论的铺垫介绍了，下一讲我们将详细分析pf文件夹里每个CPP文件的代码逻辑。
转自：5.AMCL包源码分析 | 粒子滤波器模型与pf文件夹(一) - 知乎 (zhihu.com)
posted on 2022-09-14 13:54 tdyizhen1314 阅读(289) 评论(0) 编辑 收藏 举报
