(笔记)（2）AMCL Monte Carlo Localization | 基础原理篇+配备代码讲解
什么是Monte Carlo Localization呢，中文名叫蒙特卡罗定位，权威阐述见《概率机器人》第8章，移动机器人定位:栅格与蒙特卡罗。是基于粒子滤波的定位算法。
1.粒子滤波算法与蒙特卡洛定位算法
那啥是粒子滤波(particle filter)?
参考:
粒子滤波算法:
引自《概率机器人》程序4.3 粒子滤波算法(基于重要性采样的贝叶斯滤波的一个变种)
引自《概率机器人》程序8.2 蒙特卡罗定位蒙特卡罗算法(基于粒子滤波的定位算法)
2.蒙特卡洛定位算法代码实现
论文参考：
代码引用另一位作者的:
注意运行该solution.cpp时格式如下:
g++ solution.cpp -o app -std=c++11 -I/usr/include/python2.7 -lpython2.7测试结果:
5000个粒子；面积 500*500m；迭代步骤 20 steps;
迭代20步之后:
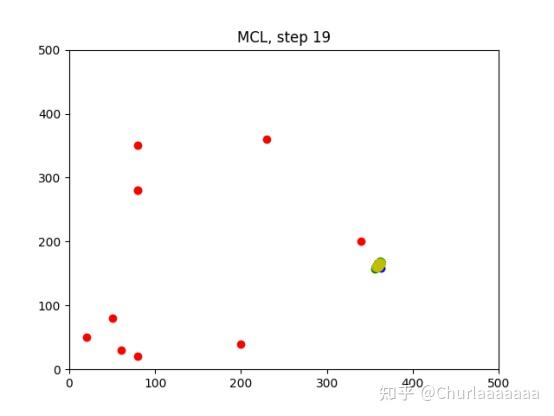
3.蒙特卡洛定位算法逻辑分析
逻辑梳理:
1.创建一个Robot对象的类，在类里规定它的一些行为，特性，当我们谈论Robot对象时，就不仅仅是myrobot了，也可以是粒子，粒子集；
Robot（) //构造函数
//Robot对象的位姿（随机给定:x,y,orient),噪声(前进噪声，转向噪声，传感器感知的噪声)；
void set(double new_x, double new_y, double new_orient)
//外部可调用此函数来给Robot对象重新设置其自身的位姿(x,y,orient)；
void set_noise(double new_forward_noise, double new_turn_noise, double new_sense_noise)
//外部可调用此函数来给Robot对象重新设置其自身的噪声(forward_noise,turn_noise,sense_noise);
vector<double> sense()
//该函数用于计算Robot对象与障碍物点(landwarks)点之间的距离，并加上传感器的测量噪声；
Robot move(double turn, double forward)
//这个函数 告诉你，这个机器人是可以动的，这里规定它的方向如何可以改变，前进的距离如何可以改变；无论如何，既然运动，那么就得加上运动噪声；
// 既然方向变了，前进距离也变了，那么位姿也跟着变了，自然地得到x,y的值；
string show_pose()
//这个函数用到to_string将double型转换成string字符串；方便你打印出Robot对象的当前时刻位姿；
string read_sensors()
//这个函数跟上一个相似，方便你打印出Robot对象当前时刻测到所有障碍物的距离集合；
double measurement_prob(vector<double> measurement)
//这个函数是核心，这里返回值是一个概率；这个概率来源于三个数据:Robot对象(粒子)与障碍物点(landmarks)的距离，传感器的测量噪声，唯一的机器人myrobot本身与障碍物点(landmarks)的距离
double x, y, orient; //robot object poses
double forward_noise, turn_noise, sense_noise; //robot object noises
private:
double gen_gauss_random(double mean, double variance)
{}
double gaussian(double mu, double sigma, double x)
{}
};2.粒子如何获得位姿:
// Create a set of particles
int n = 5000; //粒子数5000
Robot p[n];//构造一个粒子集，这个粒子集是Robot对象的一个实例化集合，具有Robot的所有行为；
for (int i = 0; i < n; i++)
{
p[i].set_noise(0.05, 0.05, 5.0);
//cout << p[i].show_pose() << endl;
}3.迭代流程,设置steps为20:
a.myrobot 运动以及感知;是的myrobot不会待在原地，它一边运动，也一边感知到周围的障碍物点(landmarks);
b.粒子群p[n]开始运动；复制myrobot的运动行为进行运动；此时粒子群p[n]经过运动之后，
位姿发生改变，我们可以换另一个粒子群对象p2[n]来暂时存放p[n]运动后的位姿，然后再令p[n]=p2[n];无它，p[n]就是个粒子集的壳；官方(《概率机器人》)操作获得粒子的位姿:
3.1 运动采样模型算法
至于这篇文章给出的代码示例，关于这部分，只是稍微做了一点变形；
Robot move(double turn, double forward)
{
if (forward < 0)
throw std::invalid_argument("Robot cannot move backward");
// turn, and add randomness to the turning command
orient = orient + turn + gen_gauss_random(0.0, turn_noise);
orient = mod(orient, 2 * M_PI);
// move, and add randomness to the motion command
double dist = forward + gen_gauss_random(0.0, forward_noise);
x = x + (cos(orient) * dist);
y = y + (sin(orient) * dist);
// cyclic truncate
x = mod(x, world_size);
y = mod(y, world_size);
// set particle
Robot res;
res.set(x, y, orient);
res.set_noise(forward_noise, turn_noise, sense_noise);
return res;
}c.粒子群p[n]到了新的地方，这时每个粒子的位置离障碍物点(landmarks)的距离肯定跟当初的距离不一样了；myrobot也运动，它的新位置离同一批障碍物点(landmarks)也不一样了；这时我们给这群可怜的粒子群p[n]一一赋予对应的粒子一个权重；该权重高的判定，取决于这个粒子是否测到障碍物群的距离与myrobot测到障碍物群的距离相似程度高。那这些粒子怎么拥有权重的具体赋值呢，来自代码里的这句 w[i]=p[i].measurement_prob(z);这个z来源，自然是来源于myrobot自己感知到的障碍物点(landmarks)了。所以，z= myrobot.sense()。至于measurement_prob（）就太值得大书特书了。官方(《概率机器人》)版本是这样计算:
3.2 观测打分模型算法
至于这篇文章给出的代码示例，关于这部分，只是稍微做了一点变形；
z的来源:
vector<double> sense()
{
// Measure the distances from the robot toward the landmarks
vector<double> z(sizeof(landmarks) / sizeof(landmarks[0]));
double dist;
for (int i = 0; i < sizeof(landmarks) / sizeof(landmarks[0]); i++)
{
dist = sqrt(pow((x - landmarks[i][0]), 2) + pow((y - landmarks[i][1]), 2));
dist += gen_gauss_random(0.0, sense_noise);
z[i] = dist;
}
return z;
}真正计算权重(其实是个概率):
double measurement_prob(vector<double> measurement)
{
// Calculates how likely a measurement should be
double prob = 1.0;
double dist;
for (int i = 0; i < sizeof(landmarks) / sizeof(landmarks[0]); i++)
{
dist = sqrt(pow((x - landmarks[i][0]), 2) + pow((y - landmarks[i][1]), 2));
prob *= gaussian(dist, sense_noise, measurement[i]);
}
return prob;
}d.在c步粒子群每个粒子都有了自己的权重了；那么在这群粒子中一定有一个粒子权重最大的代表，我们把它挑选出来，进入重采样程序里，好好用用。官方《概率机器人》介绍的低方差采样如下:
3.3 低方差采样算法
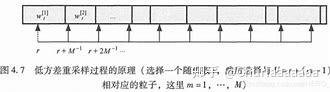
至于这篇文章给出的代码示例，关于这部分，只是稍微做了一点变形；其实我们自己也可以稍微变一变；
//Resample the particles with a sample probability proportional to the importance weight
Robot p3[n];
int index = gen_real_random() * n;
cout << "index: " << index << endl;
double beta = 0.0;
double mw = max(w, n);//瞧，我们选出的那个lucky粒子，它具有最大的权重；
cout << "mv:" << mw << endl;
//注意对比看上面的低方差采样 第6行: for m=1 to M do ;
for (int i = 0; i < n; i++)
{
beta += gen_real_random() * 2.0 * mw;//
//注意对比看上面的低方差采样 第8行：while U > c;
//而U是第7行 : U = r +(m-1).M^-1;这里我们对应beta,把beta的赋值改得稍微有点不一样；
//不过还是依旧带有随机性并且携带lucky粒子的权重；
while (beta > w[index])
{
beta -= w[index];
index = mod((index + 1), n);
}
p3[i] = p[index];
//cout << "changed i:" << i << " p3[i].show_pose() with index: " << index << p3[i].show_pose() << endl;
}
for (int k = 0; k < n; k++)
{
p[k] = p3[k];
//cout << p[k].show_pose() << endl;
}呵，p3[n]也只是个暂时存放p[n]经过重采样后的位姿的壳，存放完，然后又赋值给p[n];
至此，迭代流程就到这里了；
4.这群可怜的粒子 跟着myrobot一起，带着噪声运动，带着噪声感知，它们之间还要进行权重的pk，从中选出一个权重最大的lucky粒子，我们参考这个lucky粒子的权重，选择某种具有随机性质的采样方法，尽可能地用这个lucky粒子所带有的权重，再把整个粒子集再刷新一遍它们的位姿，其实也就是挪个位置继续待着，等着myrobot继续蹦迪运动，它们也老老实实跟着myrobot继续蹦迪，嘿~位置越靠近myrobot的那就是myrobot的brothers!myrobot想，既然是来了的都是brother,我们最后势必要紧紧地抱在一起....
4.总结
这篇文章是一个很基础的粒子滤波用于定位的原理+代码讲解版本。要看这群粒子跟着机器人继续蹦迪，更深入的版本，进入实用阶段，那就得换个真实场景的地图，障碍物也变了，桌子腿，柜子什么都有，我们需要通过激光扫描障碍物来告诉大家障碍物的位置，但是激光来源于激光传感器，它有时靠谱，有时也不靠谱；粒子数那么多，一个数组也存不下了，那就换一个更好的数据结构-KDtree来存；重采样也不能这么随意简单了，得换plus版。但是万变不离宗，总之就是一群粒子跟着机器人蹦迪，离机器人越近，那就是机器人的兄弟，我们会紧紧拥抱在一起，不分离。
转自：2.Monte Carlo Localization | 基础原理篇+配备代码讲解 - 知乎 (zhihu.com)
posted on 2022-09-14 13:48 tdyizhen1314 阅读(612) 评论(0) 编辑 收藏 举报
