朴素贝叶斯分类模型

一、一些数学基础

  首先我们总结一下有关朴素贝也斯中遇到的概率知识。

1. 条件概率

定义   若\((\Omega,F,P)\) 是一个概率空间，\(B \in F\),且\(P(B)>0\),对任意的\(A \in F\)，称

\[P(A|B)=\frac{P(AB)}{P(B)} \]

为在事件\(B\)发生时，时间\(A\)发生的条件概率。设\(P(A)>0\),则可以得到乘法公式

\[P(AB)=P(A|B)P(B) \]

2. 全概率公式

定义   设\(\Omega\)为实验\(E\)的样本空间，\(A\)为\(E\)的事件，\(B_1,B_2,...,B_n\)为\(\Omega\)的一个划分，且\(P(B_i)>0\),则有

\[P(A)=P(A|B_1)P(B_1)+P(A|B_2)P(B_2)+...+P(A|B_n)P(B_n)=\sum_{i=1}^n{P(A|B_i)P(B_i)} \]

当\(n=2\)时，原式可以写成

\[P(A)=P(A|B)P(B)+P(A|\overline{B})P(\overline{B}) \]

全概率公式可以将复杂的概率问题分解为若干个简单的概率问题，然后利用概率可加性求出结果。

3. 贝叶斯公式

定义   设\(\Omega\) 为式验\(E\)的样本空间，\(A\)为\(E\)的事件，\(B_1,B_2,...,B_n\)为\(\Omega\)的一个划分，且\(P(A)>0,P(B_i)>0\),则

\[P(B_i|A)=\frac{P(A|B_i)P(B_i)}{\sum_{j=1}^nP(A|B_j)P(B_j)} \quad i=1,2,...,n \]

上述公式是显然的，由条件概率公式的得到

\[P(B_i|A)=\frac{P(AB_i)}{P(A)} \]

分子用乘法公式替换\(P(AB_i)=P(A|B_i)P(B_i)\),分母用全概率公式替换\(\sum_{j=1}^nP(A|B_j)P(B_j)=P(A)\)，同样的，我们不难直接得到贝叶斯定理

\[P(A|B)=\frac{P(B|A)P(A)}{P(B)} \]

二、朴素贝叶斯分类原理

  朴素贝叶斯分类是一种十分简单的分类算法，叫它朴素贝叶斯分类是因为这种方法的思想真的很朴素，朴素贝叶斯的思想基础是这样的：对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类项属于哪个类别。通俗来说，就好比这么个道理，你在街上看到一个黑人，我问你你猜这哥们哪里来的，你十有八九猜非洲。为什么呢？因为黑人中非洲人的比率最高，当然人家也可能是美洲人或亚洲人，但在没有其它可用信息下，我们会选择条件概率最大的类别，这就是朴素贝叶斯的思想基础。（参考博文）

 朴素贝叶斯的正式定义如下：

1. 设\(x=\{a_1,a_2,...,a_m\}\)为一个待分类项，其中\(a_i\)为\(x\)的第\(i\)个特征属性
2. 有类别集合\(C=\{y_1,y_2,...,y_n\}\)
3. 计算概率\(P(y_1|x),P(y_2|x),...,P(y_n|x)\)
4. 如果\(P(y_k|x)=max\{P(y_1|x),P(y_2|x),...,P(y_n|x)\}\),则有\(x \in y_k\)

 问题的关键在于计算第3步中到概率，可以用贝叶斯公式

\[P(y_i|x)=\frac{P(x|y_i)P(y_i)}{P(x)} \]

由于分母对于所有的类别都是一样的，所以我们只关心分子计算就可以了，根据以往的数据很容易就可以计算出先验概率\(P(y_i)\),计算\(P(x|y_i)\)采用公式

\[P(x|y_i)=\prod_{j=1}^m{P(a_j|y_i)} \]

上述计算方法中，我们假设了各个属性之间是条件独立的，因为这样的假设，所以概率计算就变得简单起来。

注意条件独立和独立是不一样的，上述的条件独立是指在\(y_i\)发生的条件下，\(a_j\)是相互独立的。

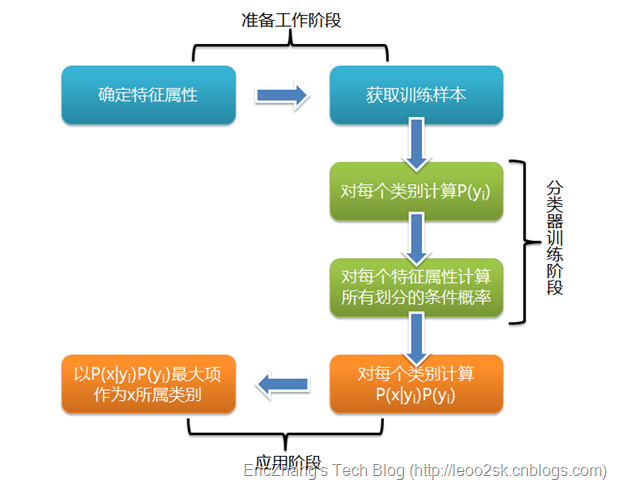
三、估计类别下特征属性划分的条件概率及Laplace校准

这里主要说说\(P(a_j|y_i)\)的估计。当属性是离散值时，只要很方便的统计训练样本各个划分在每个类别中出现的频率就可以来估计\(P(a_j|y_i)\),计算公式为

\[P(a_j|y_i)=\frac{N_i(a_j)}{N_i} \]

上式中\(N_i\)表示数据集中标签为\(y_i\)的样本个数，\(N_i(a_j)\)表示在标签为\(y_i\)的样本集中，有多少样本的第\(j\)个属性值是\(a_j\)，这样的话可能存在一些问题，我们的概率计算是连乘的，如果其中有一项\(P(a_j|y_i)=0\),那么整个概率就会为0,这样显然是很糟糕的。所以在估计\(P(a_j|y_i)\)时候需要做一个Laplace平滑处理，处理后的公式为

\[P(a_j|y_i)=\frac{N_i(a_j)+1}{N_i+C} \]

它的思想很简单，在分子加上1分母加C（类别的个数）。这样只要训练样本足够多，对结果就不会产生很大的影响。当属性的值是连续的又该怎样？此时通常假定其值服从高斯分布，即为

\[g(x,\mu.\sigma)=\frac{1}{\sqrt{2\pi}\sigma}exp\{\frac{-(x-\mu)^2}{2\sigma^2}\} \]

只要估计出\(\sigma,\mu\)就可以计算概率了。

四、总结

朴素贝叶斯算法的优点：

1. 算法逻辑简单，易于实现
2. 分类过程中时空开销小
3. 算法稳定，健壮性好

朴素贝叶斯模型假定各个属性之间条件独立的，假如各个属性的关联性很大时，该如何处理？当属性不相互独立时，朴素贝叶斯分类效果并不满意，此时可以采用半朴素贝叶斯算法，该算法大致思想是将特征相关的属性分成一组，然后假设不同组中的属性是相互独立的，同一组中的属性是相互关联的。